Roger Penrose is famous for many things, including the discovery of aperiodic tilings, the most familiar of which involves two types of rhombus:
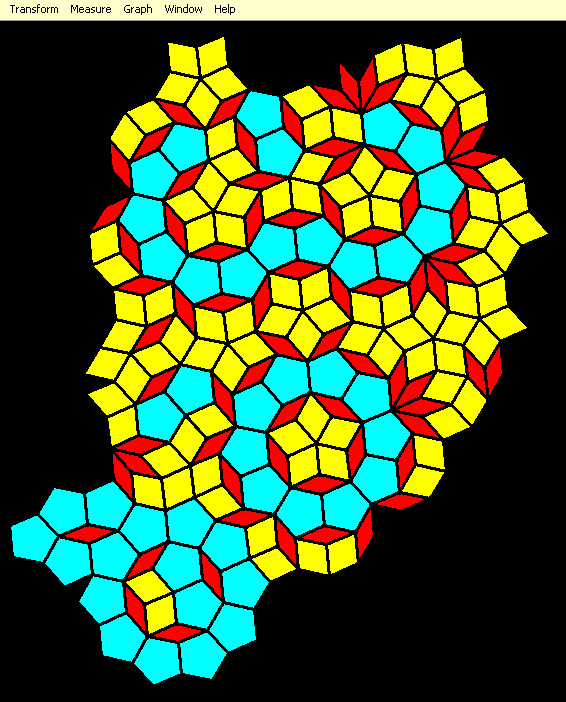
I think I have made a minor discovery about this Penrose tiling, and that is that one can add regular pentagons to it, in varying levels of pentagon-density, as shown in the first image, without it losing its aperiodicity. (I created only the first image, not the second.) I have not, however, proven this, and doubt I will.
Is this conjecture provable? I think so, but I lack the ability to write such a proof myself.
