In a kite-rhombus solid, or KRS, all faces are either kites or rhombi, and there are at least some of both of these quadrilateral-types as faces. I have found eight such polyhedra, all of which are formed by creating the convex hull of different Archimedean-Catalan base-dual compounds. Not all Archimedean-Catalan compounds produce kite-rhombus solids, but one of the eight that does is derived from the truncated dodecahedron, as explained below.

The next step is to create the compound of this solid and its dual, the triakis icosahedron. In the image below, this dual is the blue polyhedron.

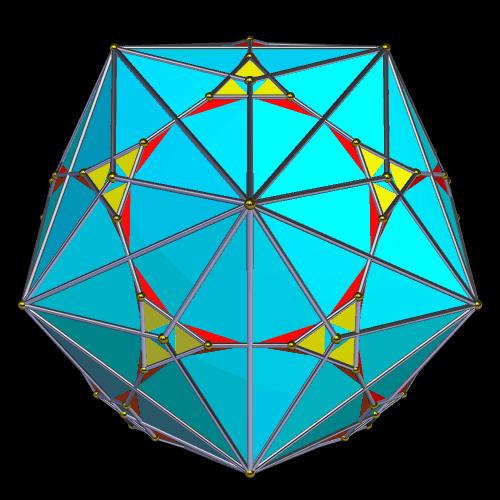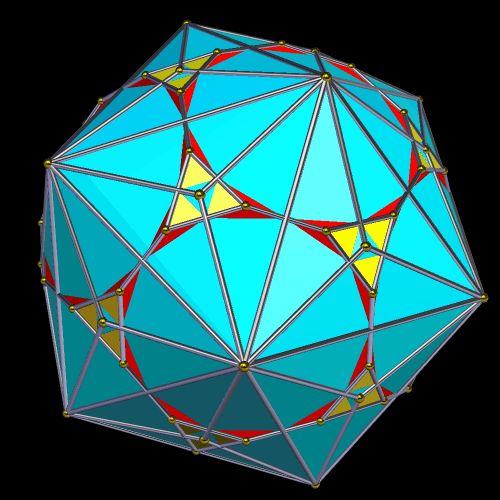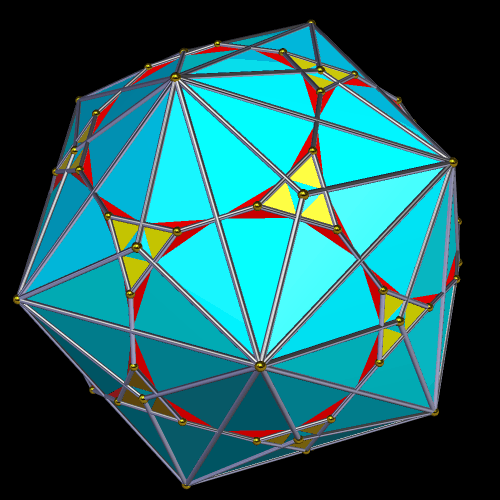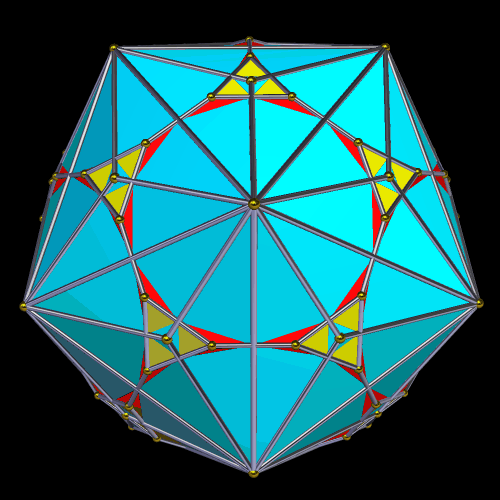
The convex hull of this compound, below, I’m simply calling “the KRS derived from the truncated dodecahedron,” until and unless someone invents a better name for it.

The next KRS shown is derived, in the same manner, from the truncated tetrahedron.

Here is the KRS derived from the truncated cube.

The truncated icosahedron is the “seed” from which the next KRS shown is derived. This KRS is a “stretched” form of a zonohedron called the rhombic enneacontahedron.

Another of these kite-rhombus solids, shown below, is based on the truncated octahedron.

The next KRS shown is based on the rhombicuboctahedron.

Two of the Archimedeans are chiral, and they both produce chiral kite-rhombus solids. This one is derived from the snub cube.

Finally, to complete this set of eight, here is the KRS based on the snub dodecahedron.

You may be wondering what happens when this same process is applied to the other five Archimedean solids. The answer is that all-kite polyhedra are produced; they have no rhombic faces. Two are “stretched” forms of Catalan solids, and are derived from the cuboctahedron and the icosidodecahedron:

If this procedure is applied to the rhombicosidodecahedron, the result is an all-kite polyhedron with two different face-types, as seen below.

The two remaining Archimedean solids are the great rhombicuboctahedron and the great rhombicosidodecahedron, each of which produces a polyhedron with three different types of kites as faces.

The polyhedron-manipulation and image-production for this post was performed using Stella 4d: Polyhedron Navigator, which may be purchased or tried for free at http://www.software3d.com/Stella.php.