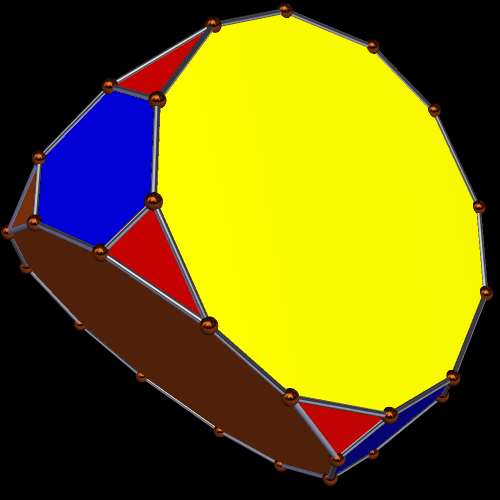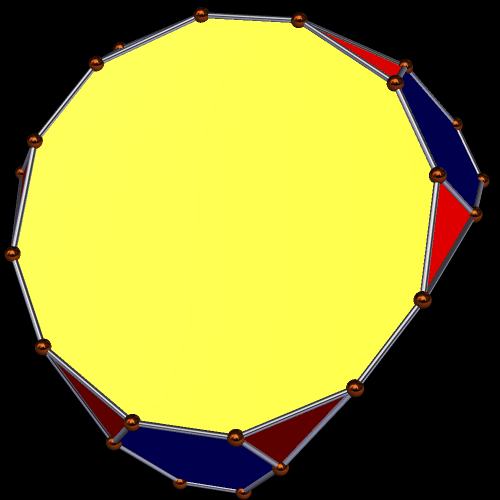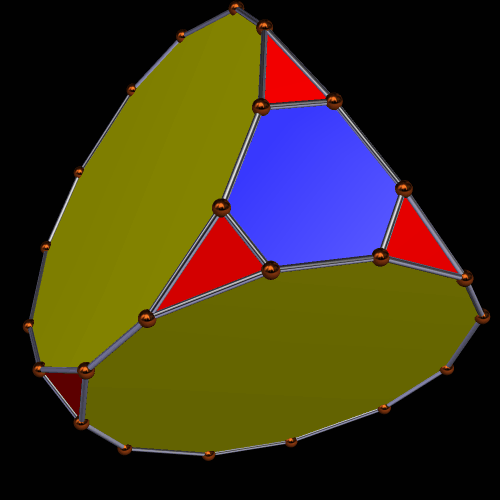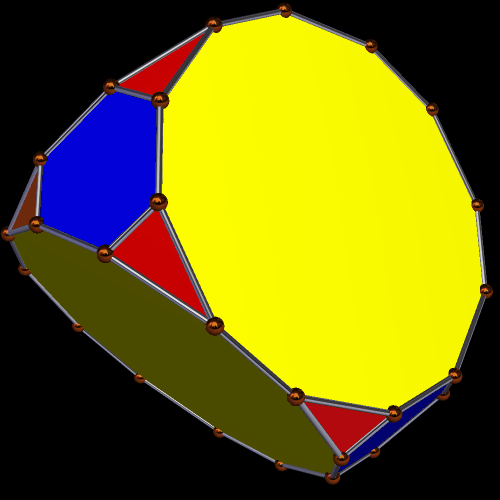
This is the result, if one performs a second truncation to the truncated tetrahedron, in such as a way as to make the resulting dodecagons regular. To do this, however, regularity of the triangles and hexagons must be sacrificed — they are merely isosceles and equiangular, respectively.
[Image made using Stella 4d, software available here.]
RobertLovesPi.net 
Ah But RobertLovesPi…if the truncation is carried our further along each relevant edge the hexagon becomes regular and the triangles become isosceles trapeziums…see Mathematical Gazette July 2012 volume 96 pp 317-323…where it is first described to my knowledge and uncovered as the underlying polyhedron in the Adidas Jabulani World Cup football in 2010. The polyhedron in now included in Mathematica’s polyhedron data set and accessed as: PolyhedronData[“JabulaniPolyhedron”]
LikeLiked by 1 person
This one? https://en.wikipedia.org/wiki/Adidas_Jabulani
LikeLike