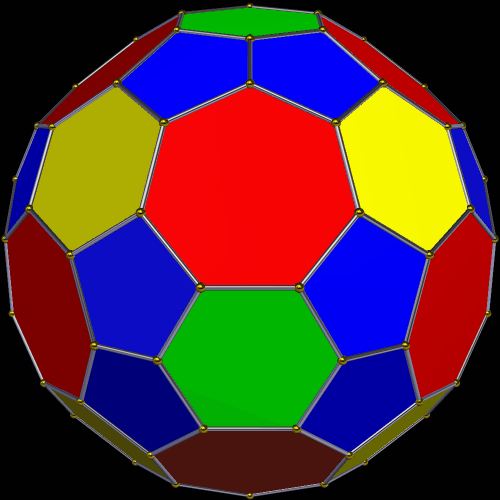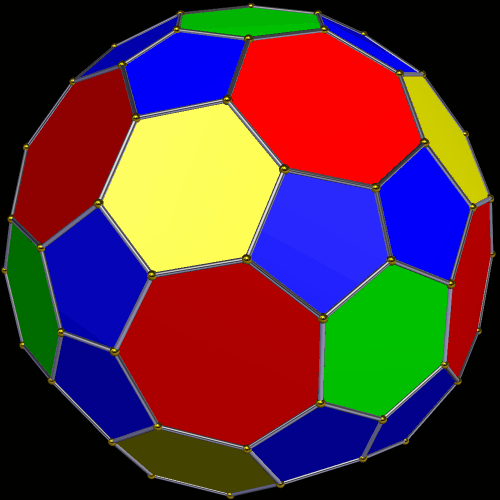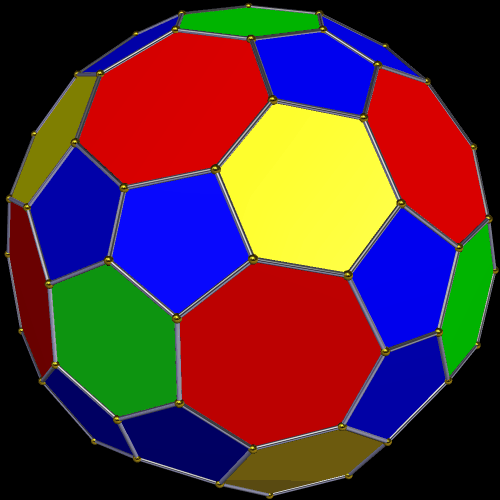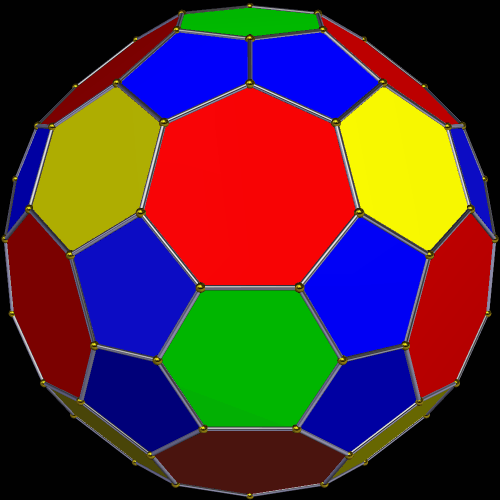
Symmetrohedra are symmetric polyhedra which have regular polygons for most (but not necessarily all) of their faces. I made this particular one using Stella 4d, which you can try for yourself at this website. Here’s the net for this polyhedron, also.
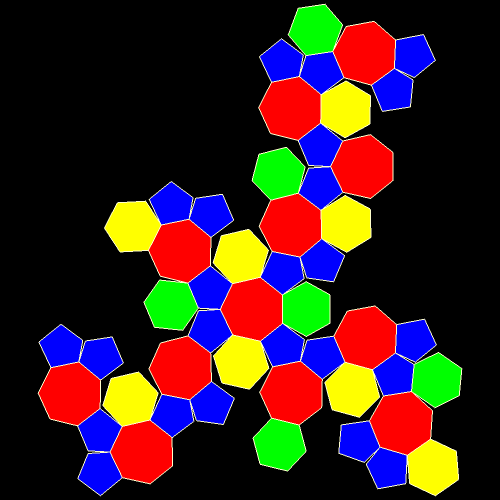
This particular symmetrohedron features twelve faces which are regular heptagons, and eight faces which are regular hexagons (shown in yellow). The irregular faces are 24 pentagons, arranged in a dozen pairs, as well as the six green hexagons. That’s 50 faces in all. This solid has pyritohedral symmetry. The most unusual thing about this polyhedron are its 12 heptagonal faces.
This one is both great and nice.
LikeLiked by 1 person
Thank you!
LikeLike
This is an extremely nice symmetrohedron because all faces have five or more sides but it’s not a fullerene. Are there any others in this group? 😁
LikeLiked by 1 person
Not that I am aware of.
LikeLiked by 1 person
Looking at it more closely, I can see how it can be derived from a different polyhedron. The bow-tie pentagon pairs start as a hexagon that’s split down the middle and then tightened into a bow-tie. This then turns any hexagon next to the bow-tie into a heptagon.
Not sure that there’s an operator that describes that transformation (turning a hexagon into a pentagon pair bow-tie), though.
LikeLike
I’m pretty sure that the polyhedron you’d derive this from would be (in Great Stella) the dual of the 3-Frequency Octahedral Geodesic Sphere. This is a 38-faced irregular polyhedron: dividing 12 of the hexagons into bow-tie pentagon pairs would then yield 24 pentagons 12 heptagons etc.
Is there a way of directly achieving this? All your stories about using Stella 4d seem to revolve around stellations / compounds / convex hulls and serendipity. Which is fun, but exceedingly indirect (as far as I can see).
LikeLike