A common definition for “Archimedean solid” goes like this: Archimedean solids (1) are convex polyhedra, (2) include only faces which are regular, convex, non-intersecting polygons, (3) have more than one type of regular polygon used as faces, and (4) have the same set of polygons meeting at each vertex, in the same pattern. Archimedes himself enumerated the thirteen Archimedean solids, noted that two of them have mirror-images, and it has been proven that no more exist . . . provided the definition above is tweaked, just a little. Why isn’t this definition adequate? Here’s why.
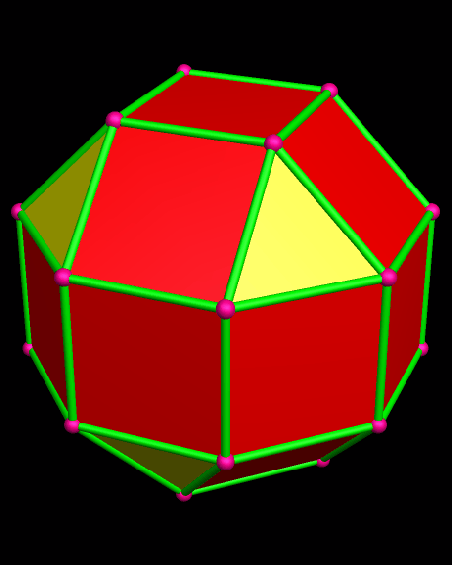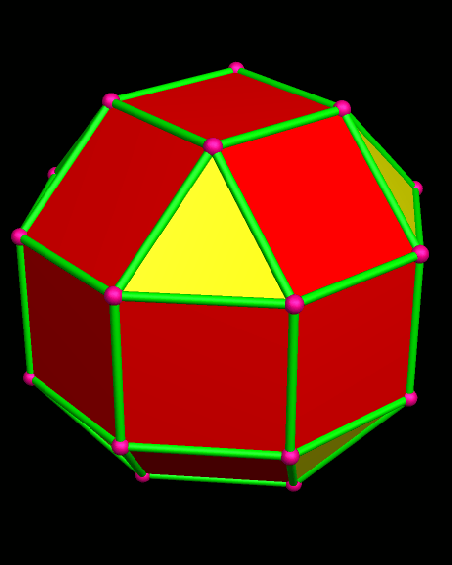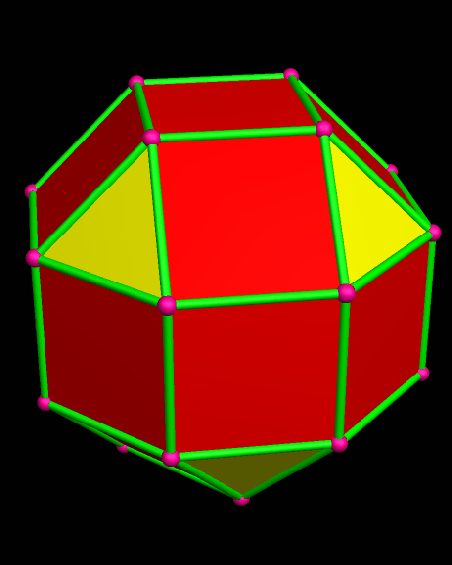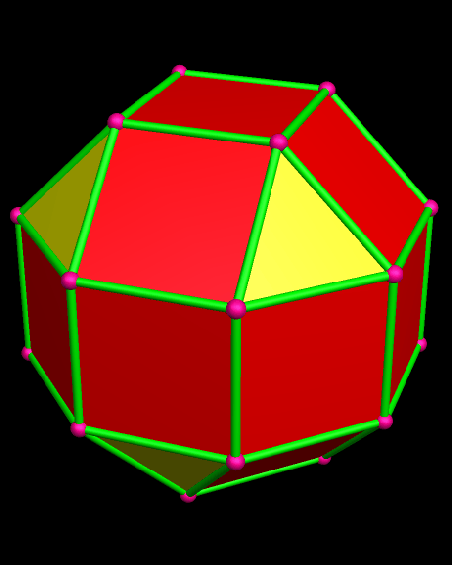
By the definition given above, both of these polyhedra qualify as Archimedean solids . . . but only the top one is included in the official set of thirteen. It’s called the rhombcuboctahedron (or the rhombicuboctahedron). Both polyhedra shown have eighteen square faces, and eight triangular faces, all regular. In each one, also, the face-pattern around each vertex is square/square/square/triangle. However, the bottom figure, despite this, is not considered an Archimedean solid. Its existence is the reason — the only reason, to my knowledge — that the definition given above for the Archimedean solids is inadequate.
When I first encountered these two polyhedra side-by-side, I was reading Peter Cromwell’s excellent book, Polyhedra, and it showed them as simple black-and-white wire-frame images. It took an embarrassing amount of time for me to spot the difference between them, so please don’t feel bad if you also are having trouble seeing it. To spot the difference, if you haven’t already, watch the triangles. In the top image, which is a true Archimedean solid, the four triangles at the top of the polyhedron stay right above the corresponding four triangles at the bottom of the same polyhedron. In the second image, however, this is not the case, due to a 45° rotation of the bottom “cap” of the polyhedron shown.
To fix this problem, and exclude the second figure, an extra requirement has been added to the list that defines the Archimedean solids: not only must each vertex be locally identical, but there must also be a global isometry shared by all vertices. In lay terms, that means that you can look at any vertex you choose, and see the same pattern for the other vertices, their orientation relative to each other, and the orientation of the faces surrounding them, as well. The first polyhedron shown here passes this test, but the second does not.
This troublesome-but-interesting second polyhedron has several names. I usually call it the pseudorhombcuboctahedron. Other names include the pseudorhombicuboctahedron (note the extra “i”), and Miller’s solid (based on the work of J.C.P. Miller, as described in Cromwell’s book). As #37 in Norman Johnson’s set of 92 Johnson solids, of which it is unambiguously a member, it is called the elongated square gyrobicupola. Finally, there are people who disagree with what I have written above . . . and they often refer to the bottom polyhedron shown as, simply, “the fourteenth Archimedean solid.”
Image credit: both pictures above were generated using Stella 4d, software you can buy, or try for free, at www.software3d.com/Stella.php.

The ancient Greeks performed geometric constructions with only a simple compass and straightedge. See how to construct an inscribed regular octagon & decagon in a circle using a compass and straightedge and how these polygons can be used to form Archemedean Solids: http://www.glennwestmore.com.au/the-archimedean-solids/
LikeLiked by 1 person
Thank you for this article! I was going mad trying to figure out the difference and why the elongated square gyrobicupola was not considered Archimedean.
LikeLiked by 1 person