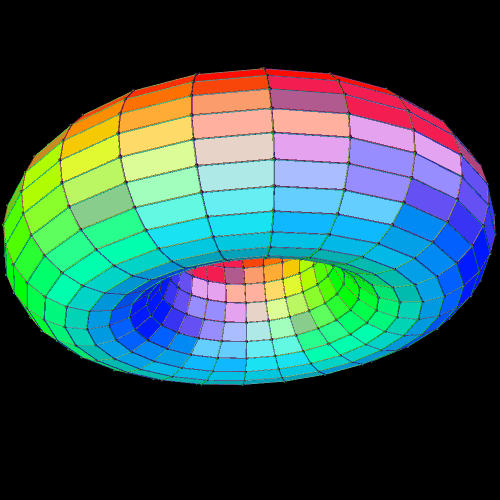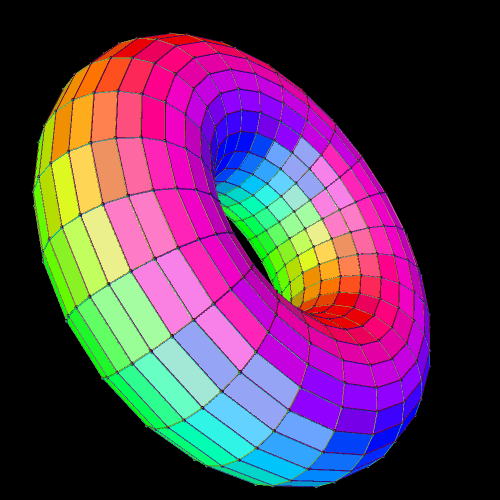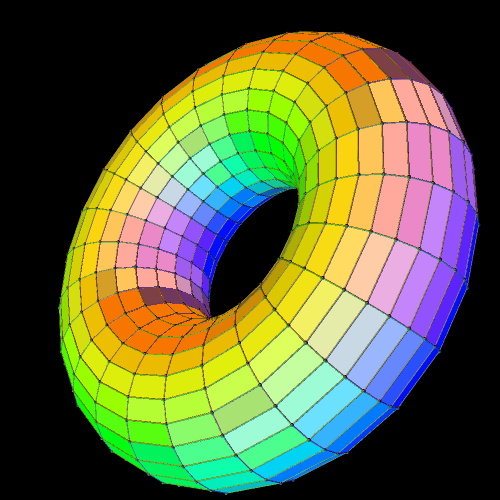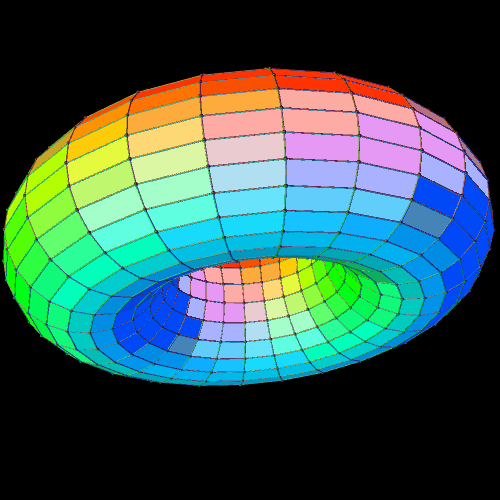
The torus is a familiar figure to many, so I chose a quick rotational period (5 seconds) for it. The dual of a torus — and I don’t know what else to call it — is not as familiar, so, for it, I extended the rotational period to 12 seconds.
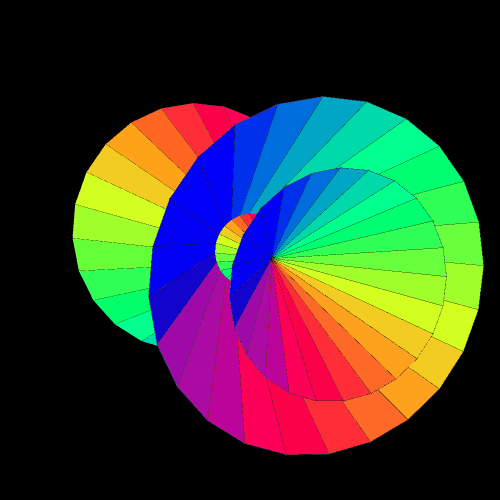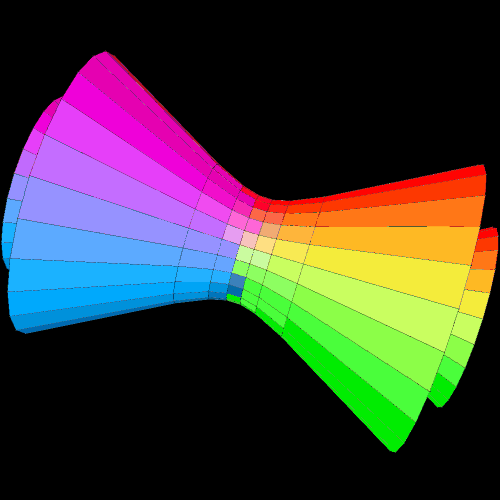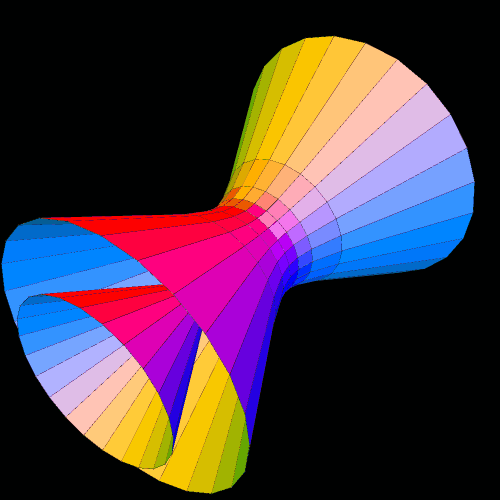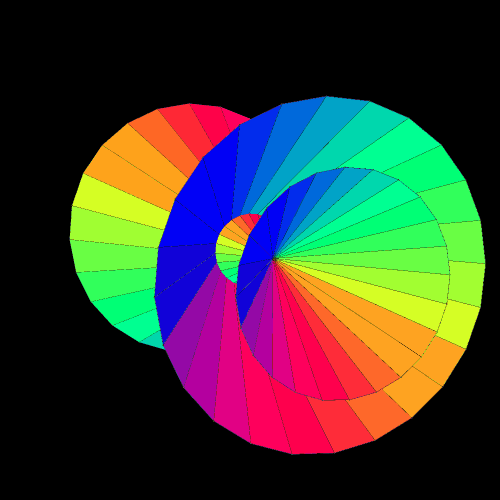
By viewing the compound of the torus and its dual, one can see the the dual is the larger of the two, by far:

I used Stella 4d to make these images. It’s a program you can buy, or try for free, at this website: http://www.software3d.com/Stella.php.
Question: Dual as in what sense?
LikeLiked by 1 person
In the same sense that a cube and an octahedron are duals, or an icosahedron and a dodecahedron are duals. In a dual pair, the positions of faces and vertices are transposed, in a difficult-to-explain way, over edges, with the edges of one figure perpendicular to the edges of its dual. Stella renders tori (and their duals) with many flat faces, not one smoothly-curving surface. Now that you bring it up, I’m not certain the concept of duality would survive the transition to smoothly-curving surfaces, or how it would be altered if it did survive. I will need to investigate this further.
LikeLike
it’s make me happy and positive
LikeLiked by 1 person
Out of sheer curosity how does the volumr between the two cones change?
Thanks
Ashok
LikeLiked by 1 person
Judging from the fact that the two cones (on one side) get closer to each other in the next post, when more faces are used (to better simulate a true torus, with one smoothly curving surface), my guess is that the volume of this between-cone region is approaching a limit of zero as toroidal polyhedra and their duals approach smoothly-curving tori and their duals. In other words, the two cones approach each other, and finally meet at the limit.
LikeLike
What does the dual of the sphere look like?
LikeLike
My guess — and that’s all it is — is that the sphere is self-dual.
LikeLike