

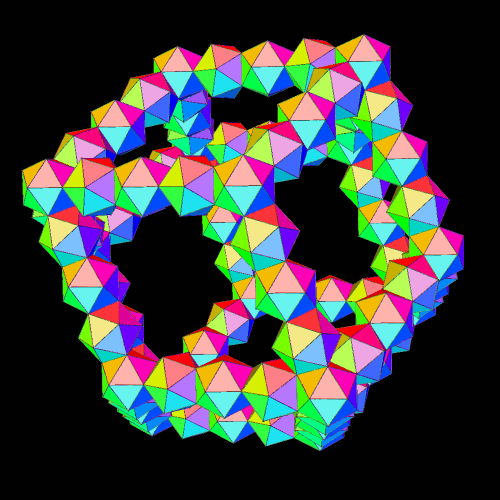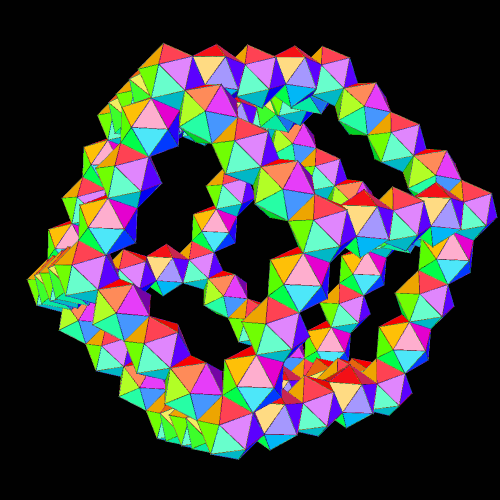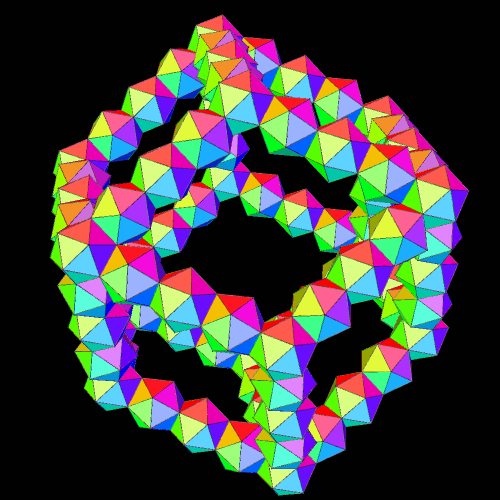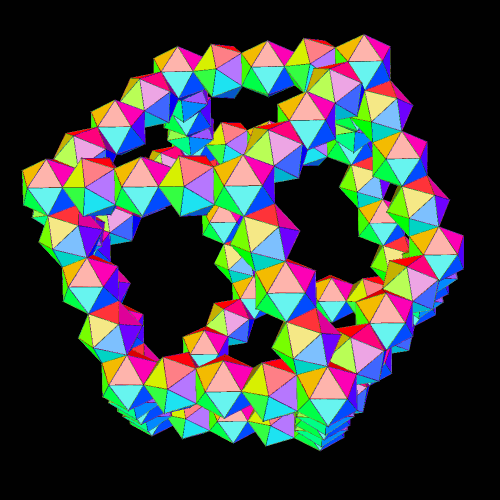
I made these using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.
Share this:
- Share on Bluesky (Opens in new window) Bluesky
- Email a link to a friend (Opens in new window) Email
- Share on Facebook (Opens in new window) Facebook
- Share on Mastodon (Opens in new window) Mastodon
- Share on Nextdoor (Opens in new window) Nextdoor
- Share on Pinterest (Opens in new window) Pinterest
- Share on Pocket (Opens in new window) Pocket
- Print (Opens in new window) Print
- Share on Reddit (Opens in new window) Reddit
- Share on Telegram (Opens in new window) Telegram
- Share on Threads (Opens in new window) Threads
- Share on Tumblr (Opens in new window) Tumblr
- Share on WhatsApp (Opens in new window) WhatsApp
- Share on X (Opens in new window) X
Fantastic! I was sure it is possible to construct rhombic triacontahedron from icosahedra, which has the same symmetry. But rhombic dodecahedron has different symmetry.
LikeLike
I think you’d need dodecahedra to build a rhombic triacontahedron. https://robertlovespi.net/2015/11/05/92-dodecahedra-arranged-as-a-single-rhombic-triacontahedron/
LikeLike
Of course yes. I mean, both dodecahedron and icosahedron have icosahedral symmetry whole rhombic dodecahedron has different cubic symmetry. And the possibility to construct a polyhedron of some symmetry from polyhedra of some different symmetry is counter-intuitive. In this case it is possible (!), but HOW did you get the idea of doing so?
LikeLiked by 1 person
I got the idea from a Zome model of the rhombic dodecahedron, which uses yellow struts, which are triangular, and attach twenty to a node — like the twenty triangles of an icosahedron.
LikeLike
Hi guys, you can notice in buckminster Fuller work that each vertices of icosahedron cuts each faces of the rhombic dodecahedron with the golden ratio. This is why this two shapes are like a bridge between thé pentagonal golden ratio geometry and the cubic or hexagonal √2 ratio geometry. This is absolutly mind blowing.
Zentou Sony
LikeLiked by 1 person