A Blue-On-Blue Rendering of the Final Stellation of the Icosahedron

Posted on 5 February 2025 by RobertLovesPi

I made this using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.

Five Views of the Compound of the Truncated Dodecahedron and the Truncated Icosahedron

Posted on 31 October 2024 by RobertLovesPi

When I let Stella 4d (a program you can try for free right here) choose the colors of this compound, here’s what I was shown.

Next, I chose “color as a compound.”

For the third view, I chose “color by face type,” which yields four colors instead of two.

The fourth model shown here shows this compound in “rainbow color mode.”

Finally, the fifth coloring-scheme I tried was “color by face, unless parallel.”

Which one do you like best? My favorite is the third one shown.

An Icosahedron, Built With Rhombic Triacontahedra and Elongated Prisms

Posted on 30 December 2023 by RobertLovesPi

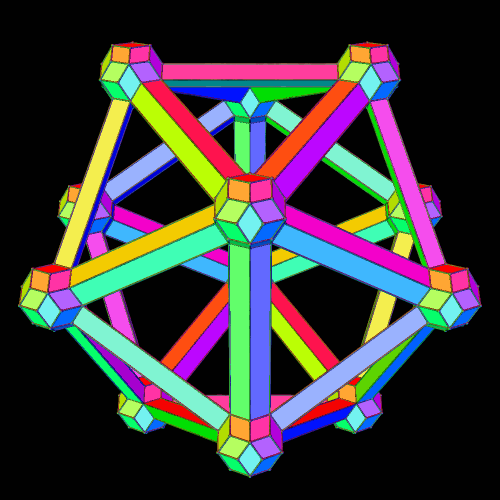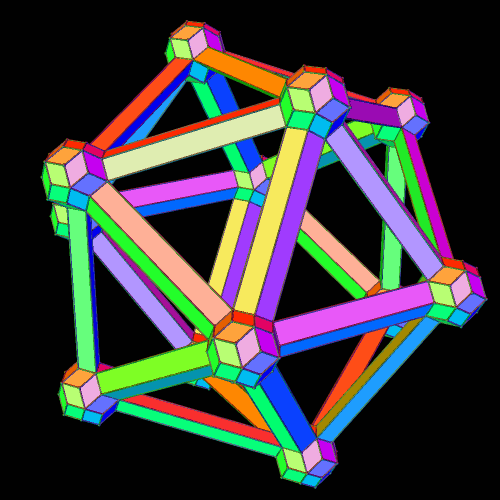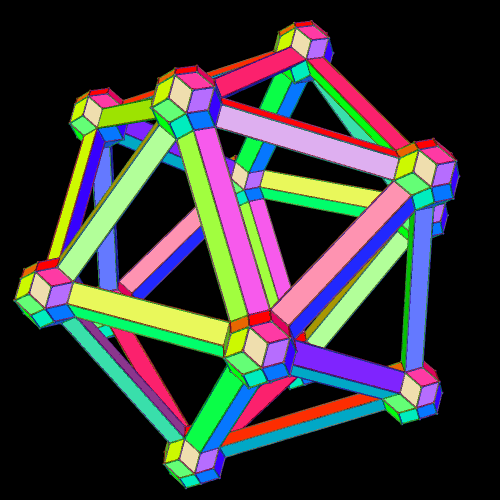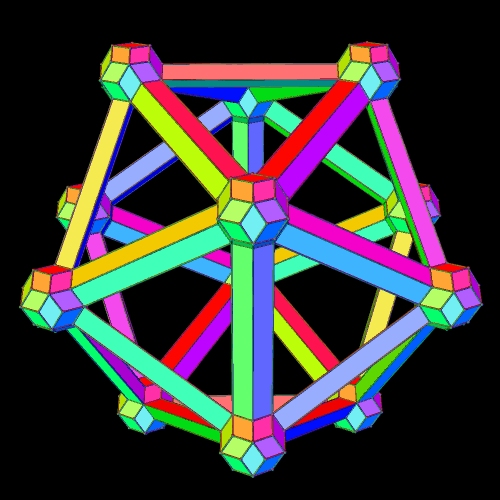
I made these two versions of the icosahedron, using rhombic triacontahedra and elongated prisms, and a program called Stella 4d. You can try this program yourself, for free, at http://www.software3d.com/Stella.php.

The Pyritohedral Golden Icosahedron

Posted on 9 January 2022 by RobertLovesPi

Both the Platonic icosahedron and the golden icosahedron have twenty triangular faces. In the Platonic version, these faces are all equilateral triangles. The golden icosahedron has eight such triangles, but the other twelve are golden triangles, which have a leg-to-base ratio which is the golden ratio. These golden triangles appear in pairs, and the six pairs are arranged in such a way as to make this a solid with pyritohedral symmetry: the symmetry of a standard volleyball.

A net for the golden icosahedron appears below. Both images were made using a program called Stella 4d, which you can try for free right here.

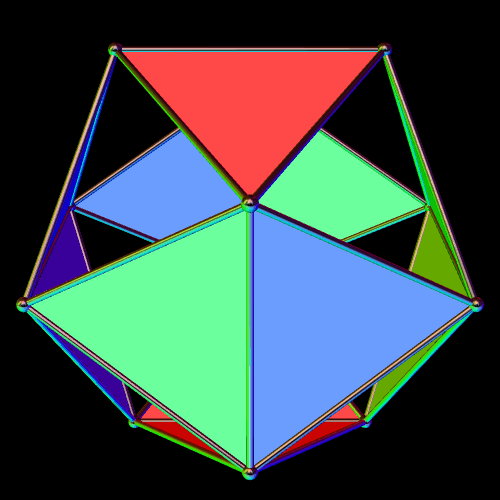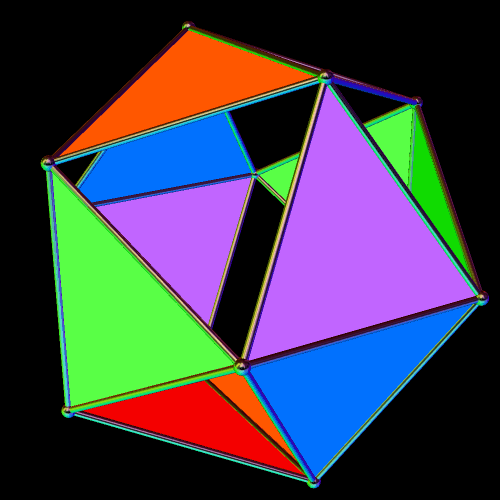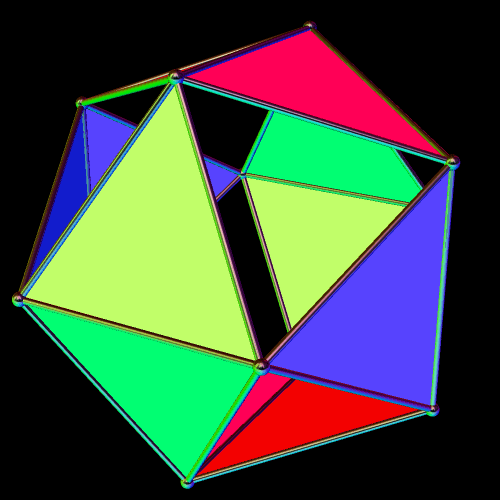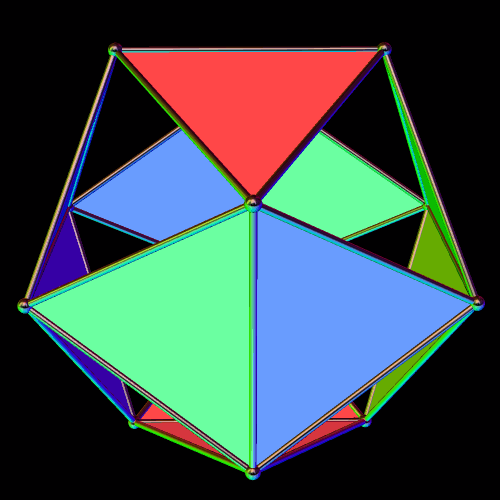
Twelve Triangles of the Icosahedron

Posted on 25 December 2021 by RobertLovesPi

Icosahedra have twenty faces. In the image above, only twelve of those triangles are visible; the other eight have been hidden, so you can see what this solid looks like on the inside. The twelve which remain have pyritohedral symmetry — the symmetry of a volleyball.

I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Toroidal Rhombic Dodecahedron, Made of Icosahedra

Posted on 17 April 2020 by RobertLovesPi

Augmented Icosa Augmented Icosa blue Augmented Icosa rainbow

I made these using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.

Spectral Icosahedra

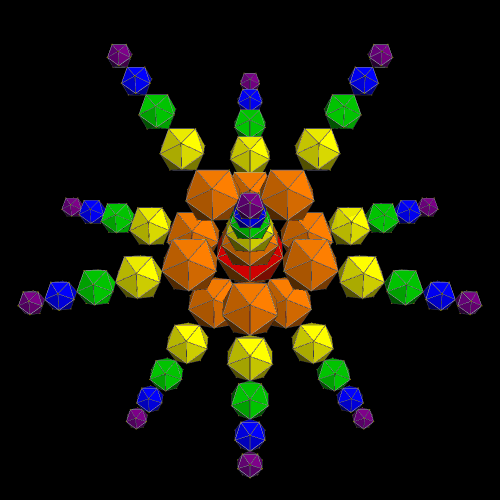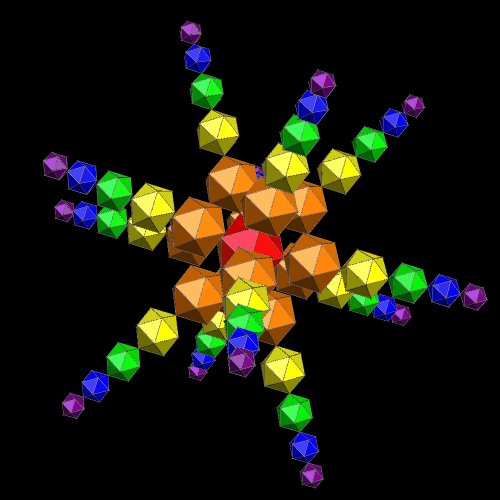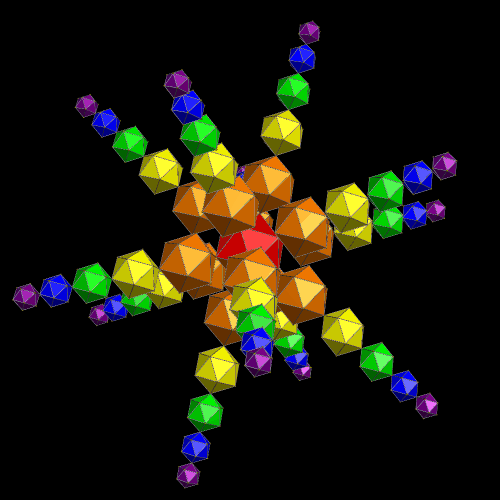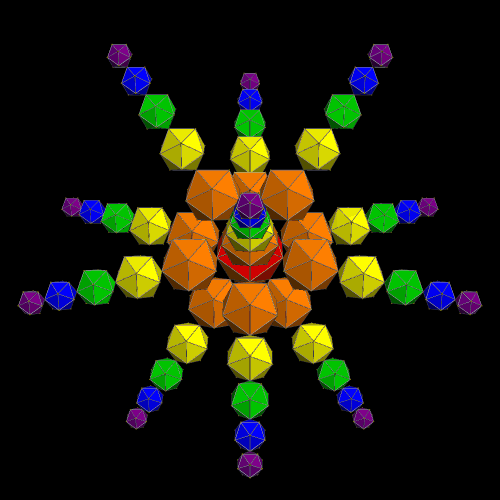
Posted on 2 February 2020 by RobertLovesPi

Stella 4d: Polyhedron Navigator has a “put models on vertices” function which I used to build this cluster of 61 icosahedra. If you’d like to try this software for yourself, there is a free trial download available at http://www.software3d.com/Stella.php.

An Embellished Icosahedron

Posted on 20 January 2020 by RobertLovesPi

Created using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Blend of the Icosahedron and the Rhombic Enneacontahedron

Posted on 22 December 2019 by RobertLovesPi

This is the icosahedron, one of the Platonic solids. It has twenty faces.

The polyhedron below is the rhombic enneacontahedron, a well-known zonohedron with ninety faces.

Finally, here is a polyhedron which blends these two. It has 20 + 90 = 110 faces.

I used Stella 4d: Polyhedron Navigator to make these images. You can try this program for free at http://www.software3d.com/Stella.php.

This Faceting of the Truncated Icosahedron is Also a Truncation of the Great Dodecahedron

Posted on 1 December 2019 by RobertLovesPi

This first version shows this polyhedron colored by face type.

In the next image, only parallel faces share a color. This is the traditional coloring-scheme for the great dodecahedron.

Both images were created with Stella 4d, which is available as a free trial download at this website. Also, the obvious change needed with this polyhedron — making its faces regular — is in the next post.