An Aperiodic Tiling of Golden Triangles and Golden Gnomons
Image
Reply
Tag Archives: tiling
Mandala Featuring Regular Heptagons and a Regular Tetradecagon, with Convex Pentagons and Isosceles Trapezoids
Image
Tessellation Involving Hexagons, Pentagons, and Other Polygons
Image
Two Versions of Mandalas Centered on Regular Octadecagons
A Golden Tessellation of Quadrilaterals
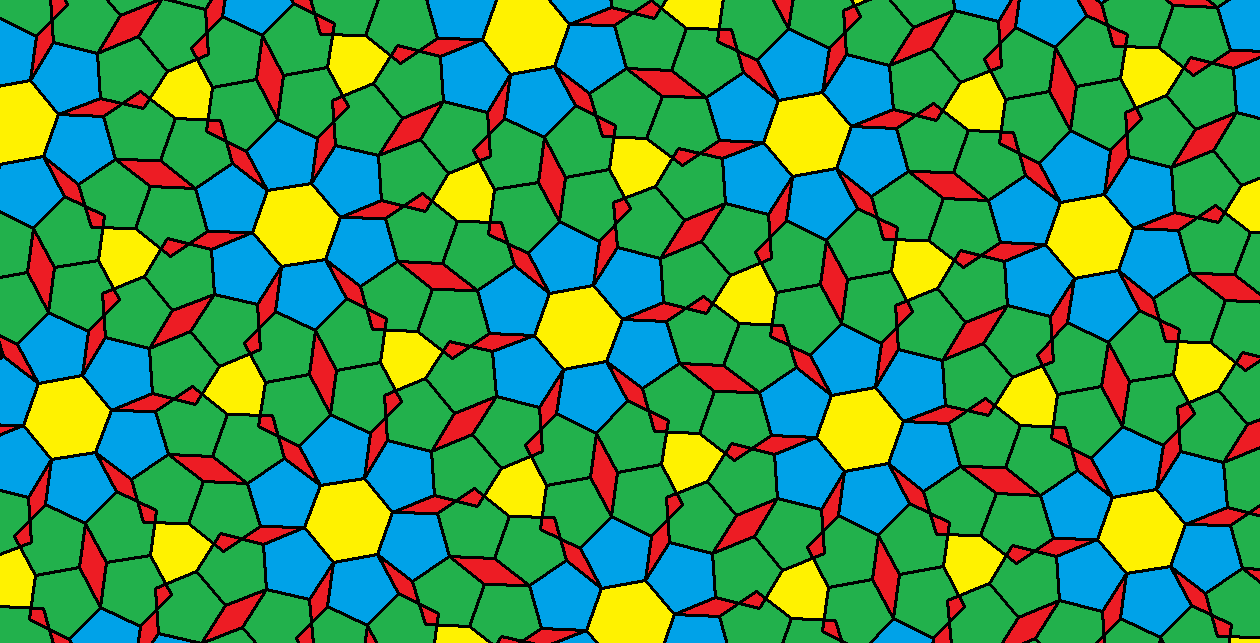
In this tessellation, golden rectangles are shown in yellow. The orange darts are each made of two golden gnomons, joined at a leg — while the blue rhombi are each made of two golden triangles, sharing a base.
Stars, Pentagons, and Rhombi #2
This is an expansion of the last post here. It may be possible to continue this tiling outward indefnitely, forming an aperioidic tiling — or it may not. I am simply uncertain about this
Floral Shield #2
This is one of the aperiodic tilings made famous by Roger Penrose.
Tiles
Image
Tessellation Featuring Regular Enneagons, Regular Hexagons, and Isosceles Triangles
Image
Tessellation Featuring Regular Enneagons and Hexaconcave, Equilateral Dodecagons
Image
RobertLovesPi.net 