Tag Archives: pentagon

Repeated Augmentations of a Dodecahedron With More and More Dodecahedra

Posted on by
3

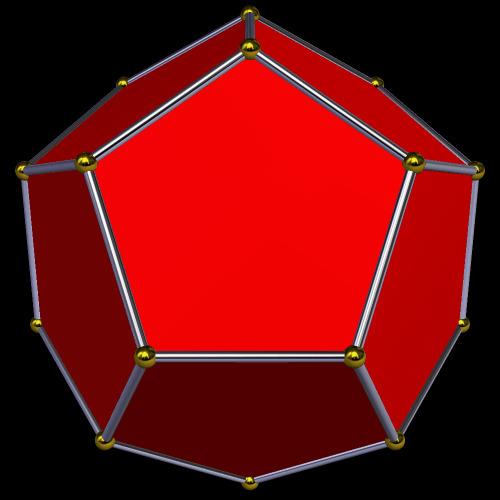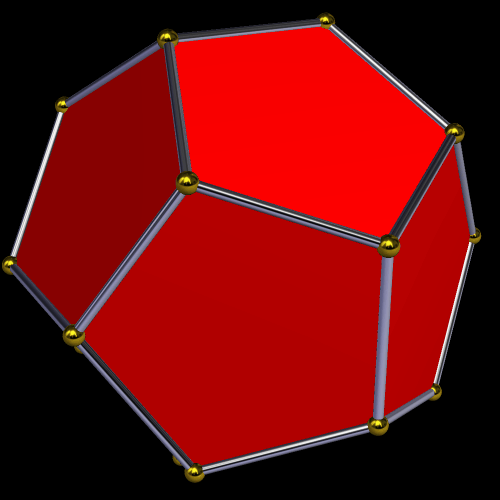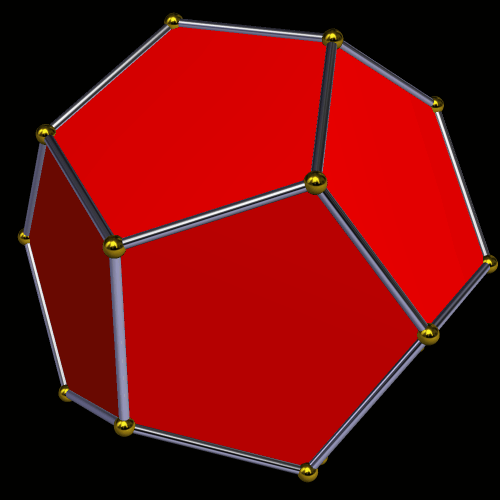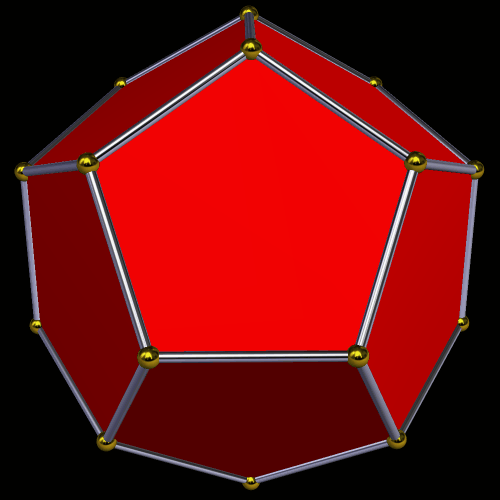
Here’s a single dodecahedron.

A new “cluster polyhedron” can be made by augmenting each pentagonal face with another dodecahedron.

If you can do it once, you can do it again, augmenting each pentagon with a new dodecahedron.

Once more.

I made these polyhedral clusters using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.

A Euclidean Construction of a Regular Convex Pentagon and a Regular Star Pentagon, Both Inscribed Inside a Given Circle

Posted on by
4
  1. Start with a (green) circle centered on A with radius AB. Point B is on this circle.
  2. Construct a line which intersects line AB at point A, in such a way that these two lines are perpendicular.
  3. This green circle intersects the newest line at two points. Designate one of these intersections as point C.
  4. Bisect segment AC, and mark point D as this segment’s midpoint.
  5. Construct a circle (the blue one) which is centered on D and includes point B.
  6. The blue circle intersects line AC at two points. Only one of these points is inside the green circle. Label this point F.
  7. Construct segment BF. This segment’s length is the edge length of the pentagon under construction.
  8. Construct a circle (the red one) which is centered on B and includes point F.
  9. The red and green circles have two points of intersection. One of them is closer to point F than the other; label this closer intersection as point I. The other point of intersection is closer to point C; label it J.
  10. J, B, and I are vertices of a regular pentagon. Construct a circle (orange) which is centered on point I and passes through point B. The orange and green circles intersect at two points, one of which is labeled B. Label the other one K. Point K is a vertex of the pentagon under construction.
  11. Construct a (purple) circle centered on K and passing through I. This purple circle intersects the green circle at two points, one of which is already labeled I. Label the other point of intersection as L. Point L is the fifth vertex of the pentagon.
  12. Connect points with segments to form regular pentagon JBIKL.
  13. Connect points with segments to form regular star pentagon BKJIL.

If I've tried this once, I've tried it at least fifty-five times….

Posted on by
4

It’s hard to get regular pentagons, regular star pentagons, regular decagons, and related polygons to tessellate the plane while maintaining radial symmetry. This is my latest attempt.

The 5/2, 5/2 Duoprism

Posted on by
Reply

I made this duoprism, a four-dimensional polytope, using Stella 4d. You can try this program for yourself, free, at http://www.software3d.com/Stella.php.