To make the image above, using Stella 4d (available here), I started with a uniform polyhedron called the small icosihemidodecahedron, and then made the triangular faces of it invisible. Here’s what this polyhedron looks like without its triangles hidden:
The convex hull of either of these figures is an icosidodecahedron, which is shown below.
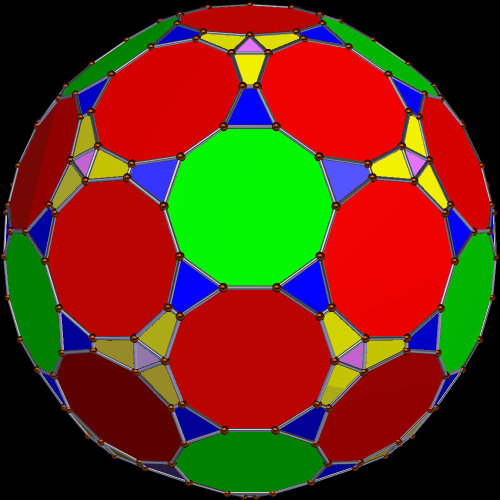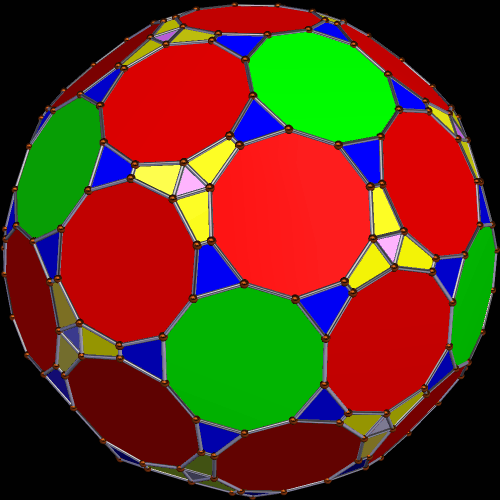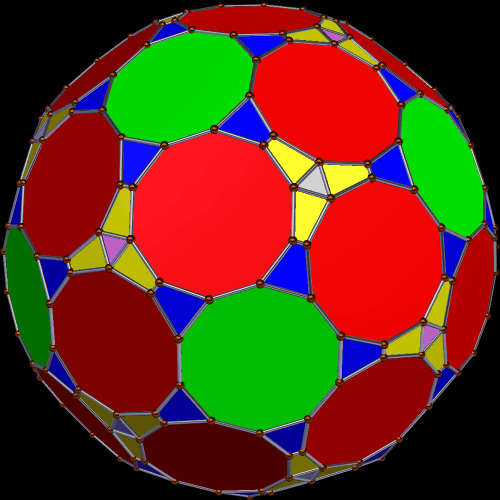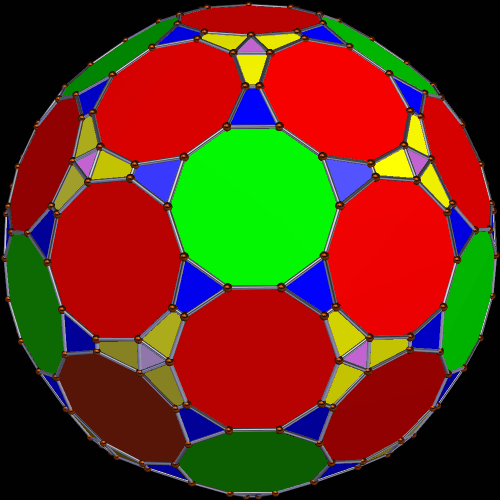
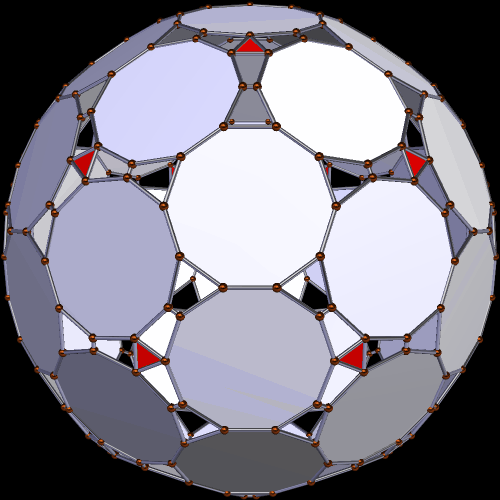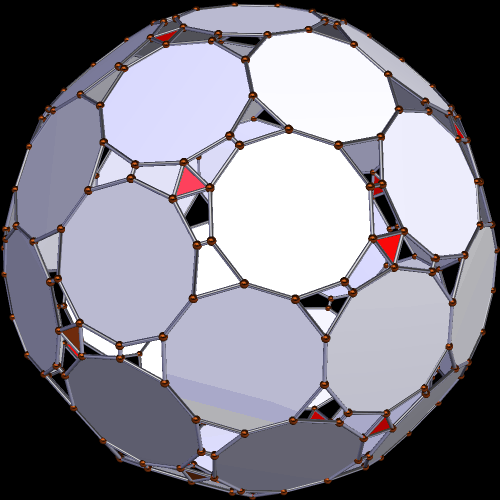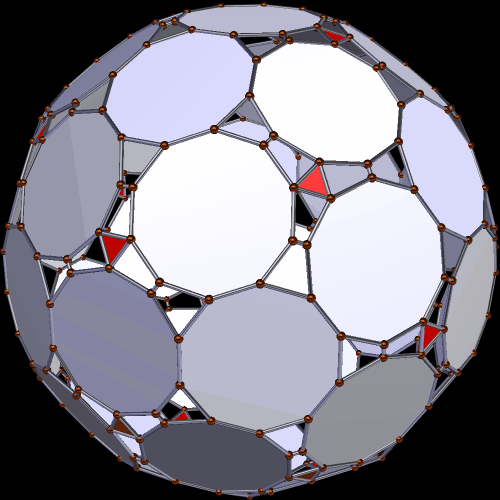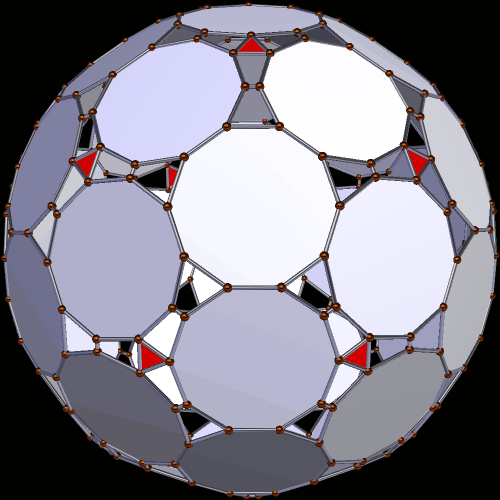
The first polyhedron shown here is also a symmetrohedron. 42 of its faces are regular decagons, and twenty are equilateral triangles. There are also sixty each of two types of isosceles trapezoids. That’s 182 faces in all.
The second polyhedron shown, below, also has 42 regular decagons as faces, along with twenty equiangular hexagons, sixty isosceles triangles, sixty almost-square isosceles trapezoids, and 120 of another kind of isosceles trapezoid. That’s a total of 302 faces.
The third one I found, shown below, has 42 decagons, sixty convex hexagons, twenty equilateral triangles, sixty rectangles, and sixty isosceles trapezoids, for a total of 242 faces.
I made all three of these polyhedra using Stella 4d: Polyhedron Navigator, which you can try for yourself, free, at http://www.software3d.com/Stella.php.
This started with a ring of ten {10/3} star decagons, and then proceeded from there.
This pattern can be extended outward indefinitely.
This decagonal mandala is split into fifty golden triangles (shown in yellow), and forty golden gnomons (shown in orange).
The black polygons in this radial tessellation are regular decagons. The red figures are hourglass-shaped equilateral hexagons, which remind me of the distinctive red markings found on many black widow spiders.
In addition to the 42 regular decagons, the faces of this polyhedron include twenty equilateral triangles, sixty yellow trapezoids, and sixty blue trapezoids. That’s 182 faces in all.
The next picture shows what happens if all of the decagons have the same color, the triangles have another, and the trapezoids are hidden from view.
Both images were created using Stella 4d, software you can try for yourself at this website.
Ten rhombic triacontahedra fit perfectly into a decagonal ring. It’s not a “near-miss” — the fit is exact.
I made this with Stella 4d, software you can try for free, or purchase, at http://www.software3d.com/Stella.php.
RobertLovesPi.net 