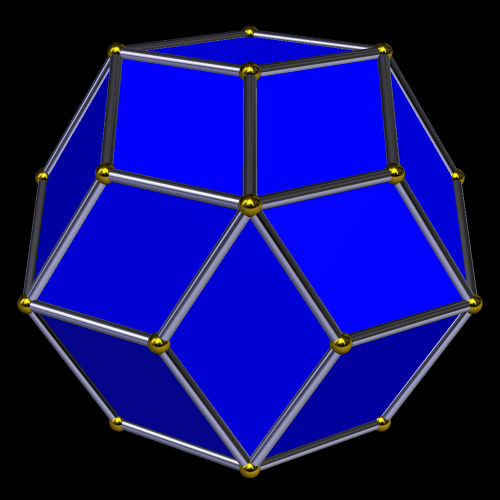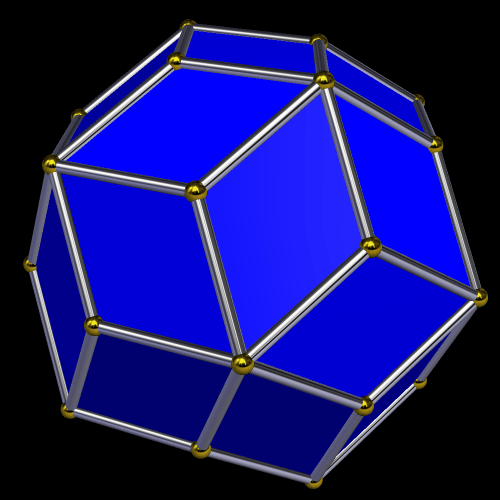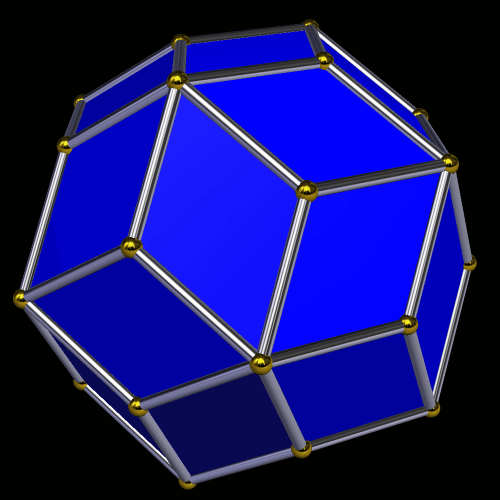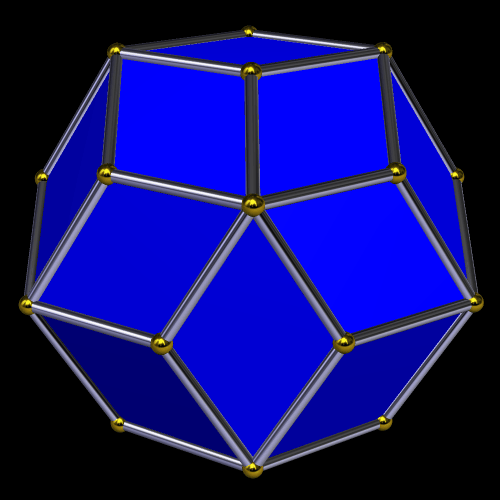
I made these compounds using Stella 4d, which you can try for free at http;//www.software3d.com/Stella.php.
Tag Archives: polyhedral
A Non-Convex Polyhedral Cluster Featuring Regular Heptagons, With a Puzzle
I stumbled upon this while playing with Stella 4d: Polyhedron Navigator, a program you can try for free at https://www.software3d.com/Stella.php. It’s difficult to herd regular heptagons.
There’s an obvious question raised by this image: what are the components of the polyhedral cluster, especially the one with heptagonal faces? Comments on this would be appreciated, especially ones with images of the components.
Clusters of Polyhedra Surrounding a Dodecahedron
The cluster below is formed by augmenting each face of the dodecahedron above with an icosidodecahedron.
Next, each triangular face is augmented with an icosahedron.
Now every pentagonal face is augmented with a dodecahedron.
Finally, the pentagonal faces in this cluster of polyhedra are augmented with icosidodecahedra. The resulting, new cluster has an overall icosahedral shape.
I did all of this using Stella 4d: Polyhedron Navigator. You can try this program for free at http://www.software3d.com/Stella.php.
The Icosidodecahedron, as Well as Two Other Polyhedra Made by Augmenting It
Here’s the icosidodecahedron — one of the Archimedean solids.
Next, here’s what this solid looks like, if you augment each pentagonal face with a dodecahedron, and each triangular face with an icosahedron.
Finally, here’s what happens if you augment each pentagonal face of this second solid with an icosidodecahedron.
I used Stella 4d: Polyhedron Navigator to create these images. You can try this program, for free, at http://www.software3d.com/Stella.php.
Clusters of Rhombic Triacontahedra
Here’s a rhombic triacontahedron, possibly the most well-known of the Catalan solids. It’s thirty faces are all golden rhombi (rhombi with their diagonals in the golden ratio).
Here’s what you get if you augment each face with another rhombic triacontahedron:
Coloring this cluster-polyhedron by face type has this result:
So what happens if each face of this cluster-polyhedron is augmented by another rhombic triacontahedron? This does:
Here’s another view of that, in “rainbow color mode”:
I made these virtual models with Stella 4d: Polyhedron Navigator. If you’d like to try this software for free, the website to visit is http://www.software3d.com/Stella.php.
A Compound of a Strombic Icositetrahedron and the Rhombic Dodecahedron

I made this using Stella 4d, which you can try for yourself, free, at this website: http://www.software3d.com/Stella.php.
A Four-Part Polyhedral Compound Derived From the Small Cubicuboctahedron

I found this compound by repeatedly stellating the small hexacronic icositetrahedron, which is the dual of the small cubicuboctahedron, one of the uniform solids. I used Stella 4d: Polyhedron Navigator to do this, and you can try this program, as a free trial download, at http://www.software3d.com/Stella.php.
A Compound of Four Hexagonal Prisms

I made this by faceting a great rhombicuboctahedron, using Stella 4d, a program you may try for free at this website: http://www.software3d.com/Stella.php.
A Compound of Four Hexagonal Dipyramids
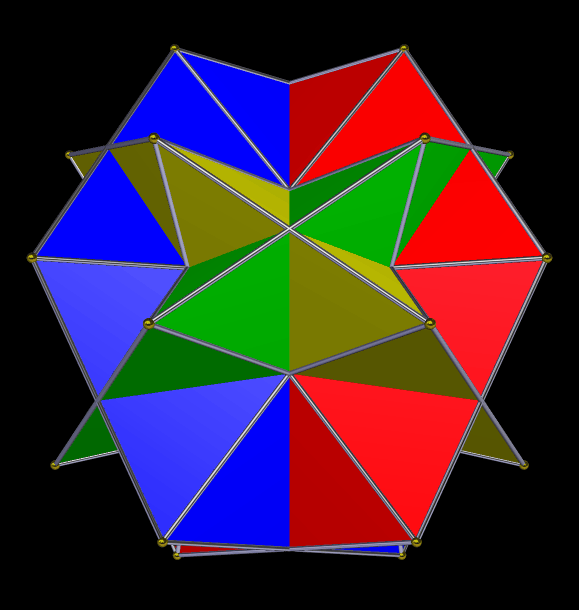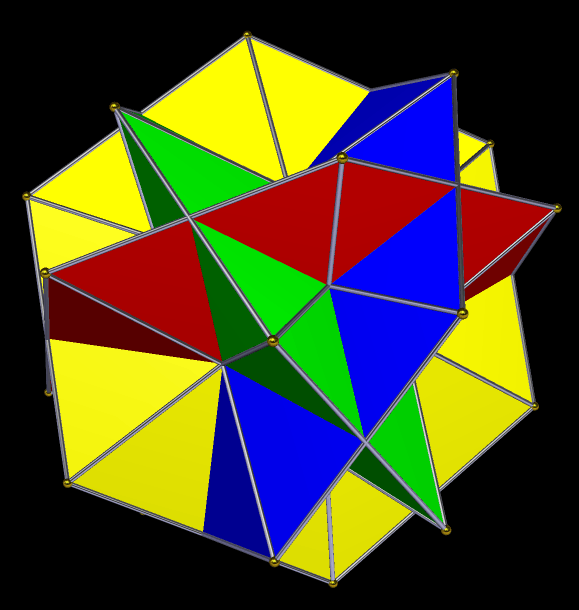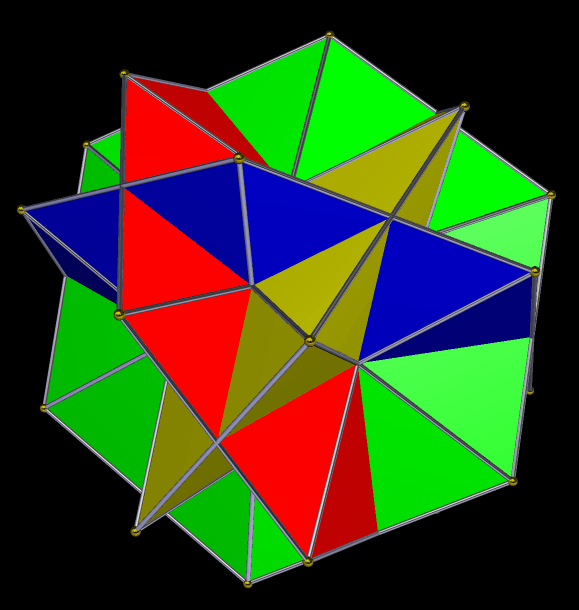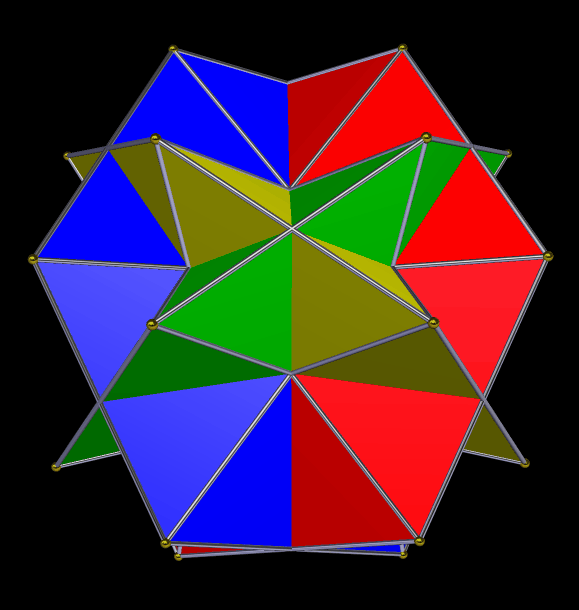
I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
Eight Different Two-Part Polyhedral Compounds
All of these were made using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.