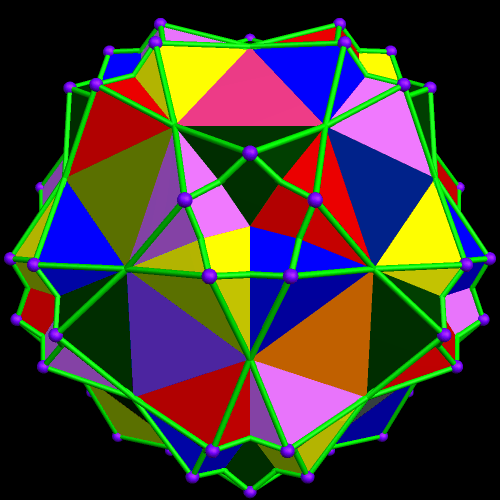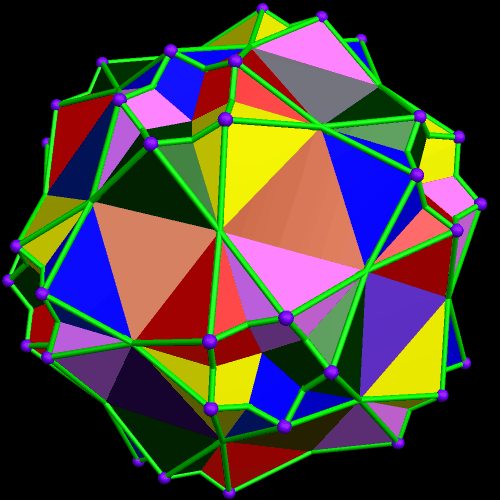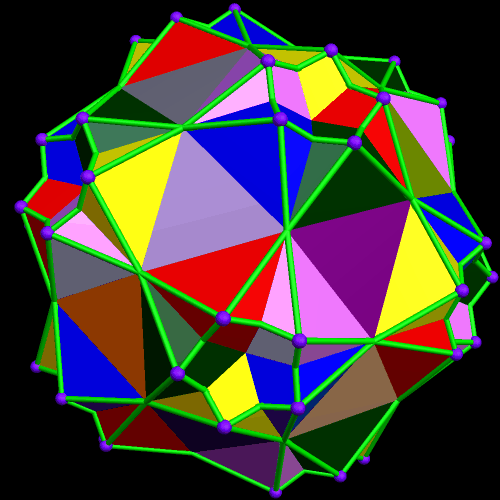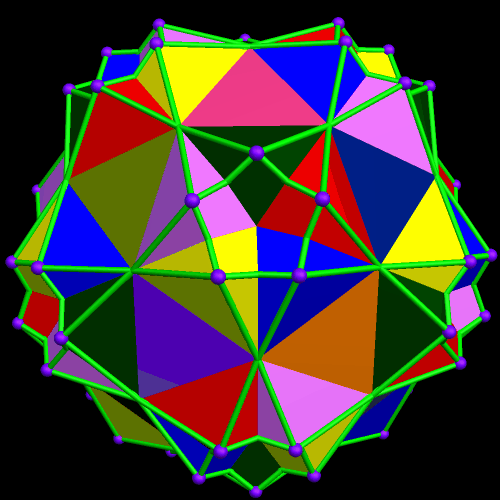
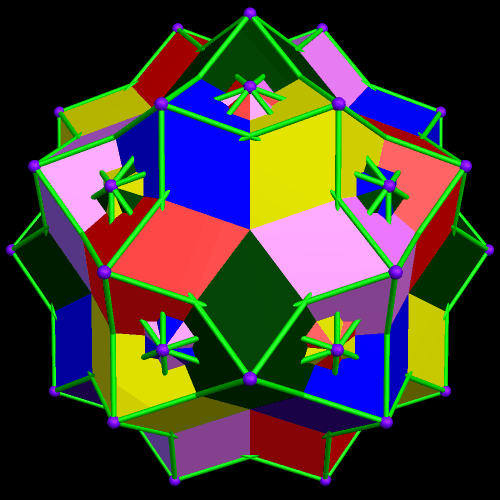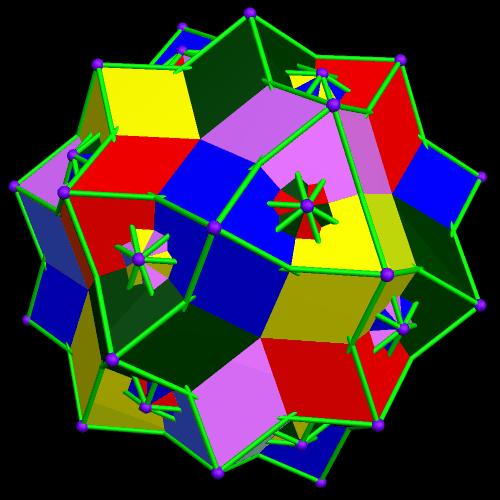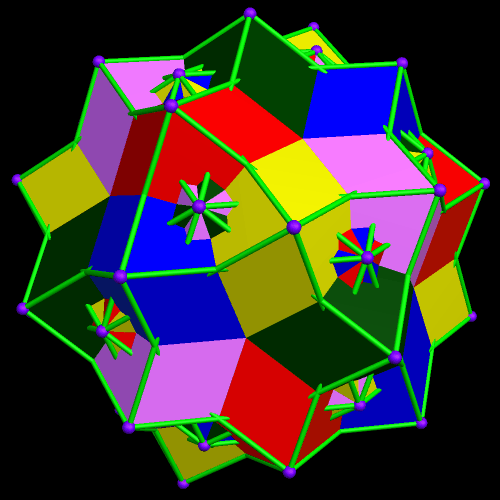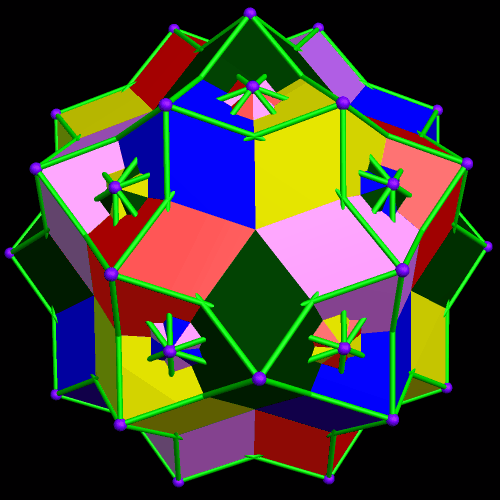
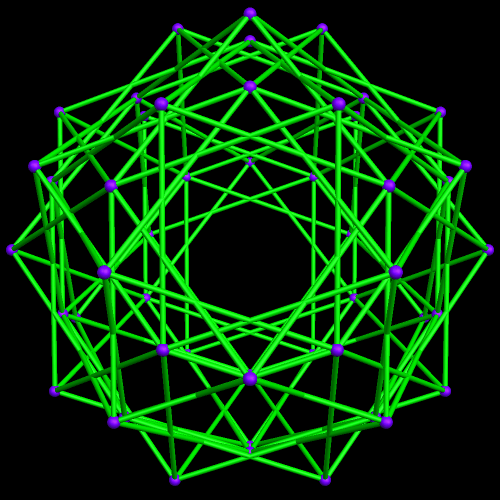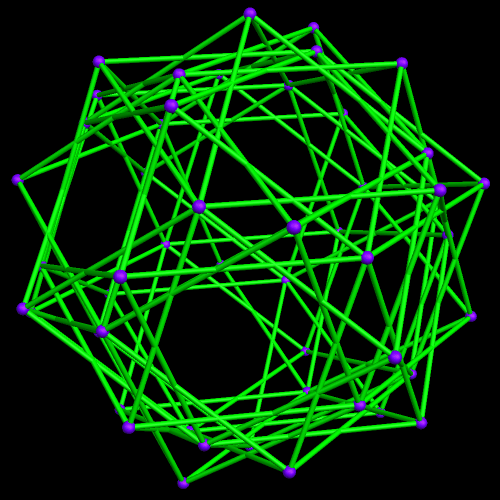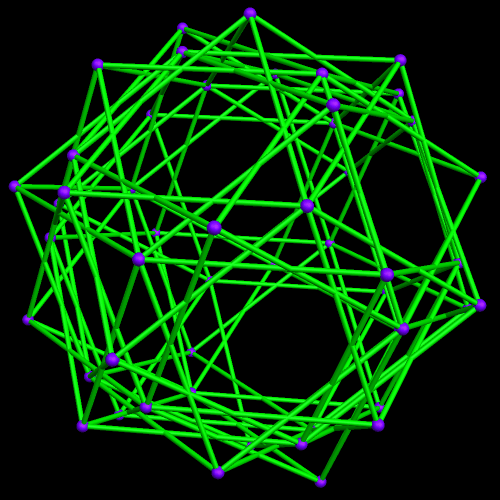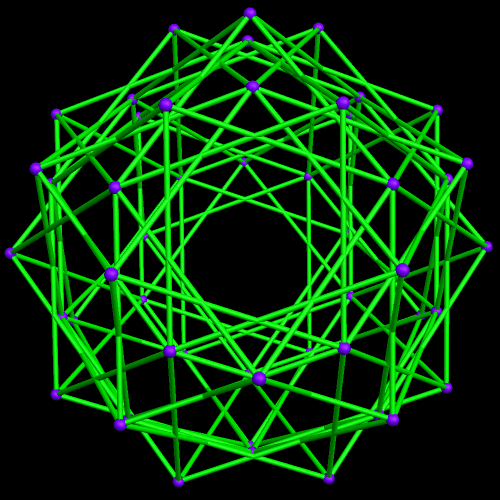
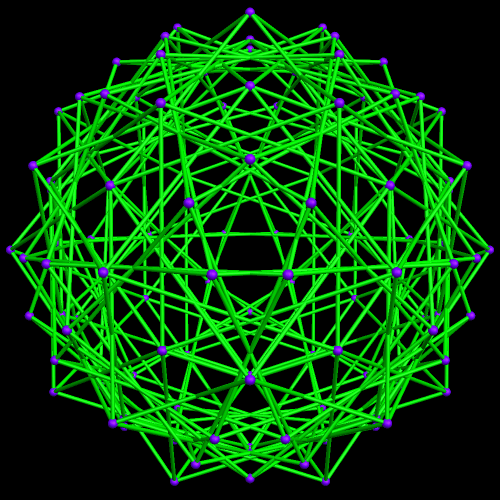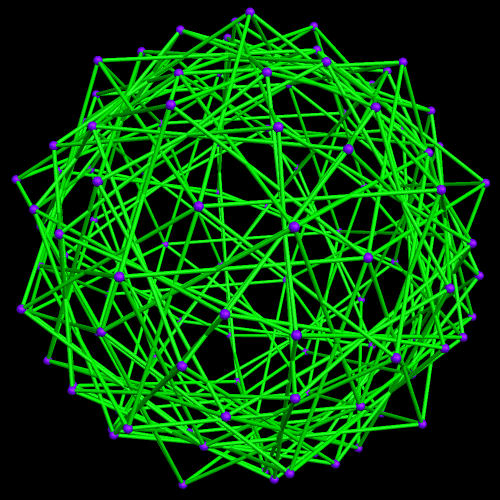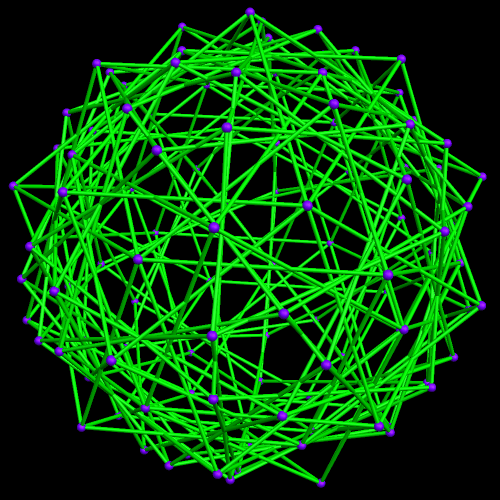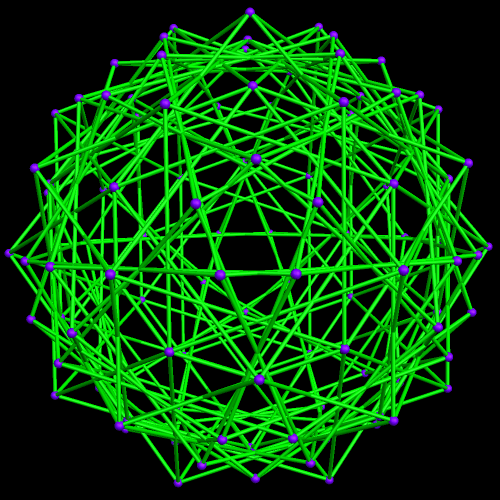
This started with a ring of ten {10/3} star decagons, and then proceeded from there.
Tag Archives: ten
The Compound of Ten Octahedra and Its Dual, the Compound of Ten Cubes
I stumbled upon the compound above while playing with facetings, starting with the rhombic triacontahedron. Here’s the compound’s dual.
I made these rotating models using Stella 4d, a program you can try for free at this website.
SpinStar
Image

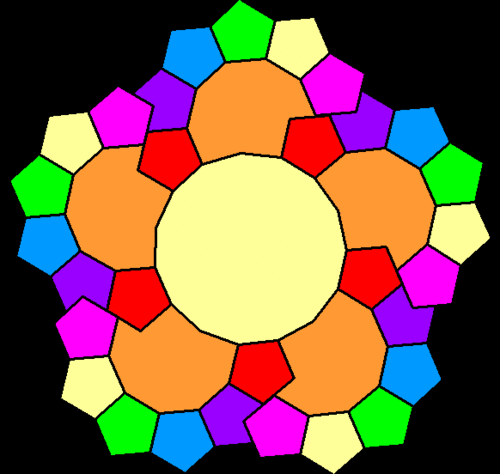
A Compound of Ten Elongated Octahedra Which Is Also a Particular Faceting of the Rhombicosidodecahedron, Together with Its Dual
Thinking about the post immediately before this one led me to see if I could connect opposite triangular faces of a rhombicosidodecahedron to form a ten-part compound — and it worked with Stella 4d just as it had when I “previewed” it in my head.

The interesting dual of the above polyhedral compound, also a ten-part compound, I was not able to preview in my head (although that would be a nice ability to have), but creating it was easy with Stella:
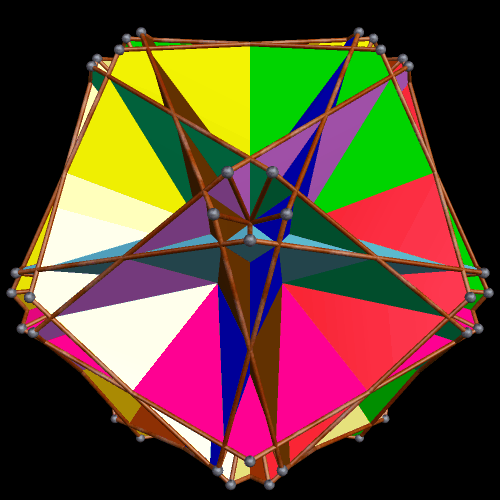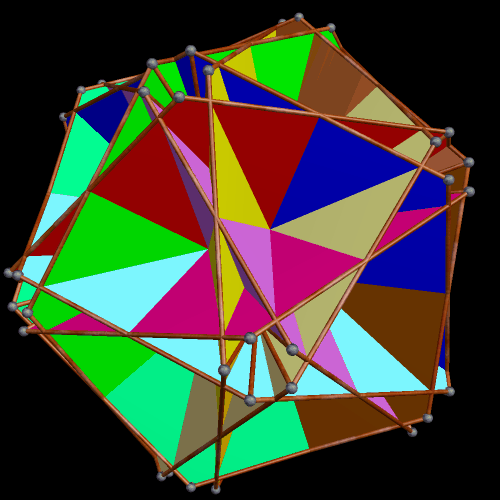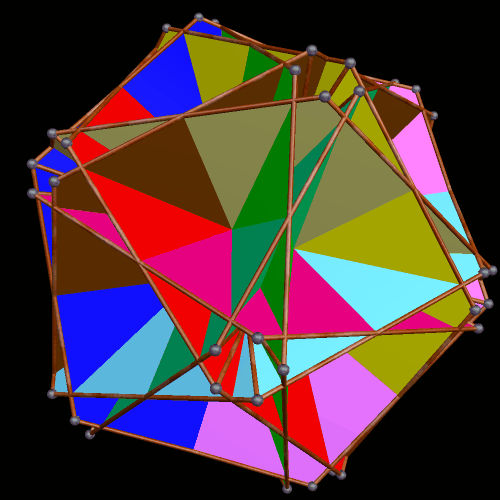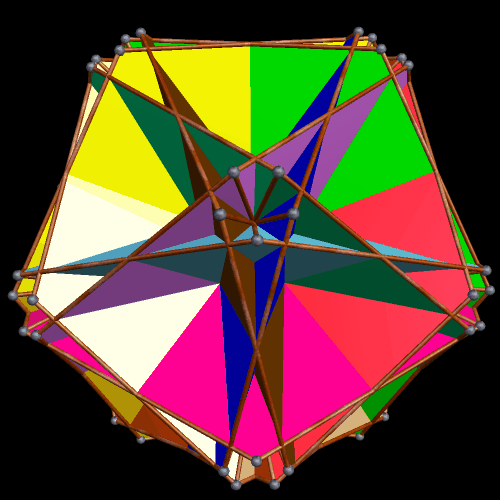
It is difficult, in the dual, to tell what the ten components are. To help with this, in the next image, all but one component has been removed. This reveals the components of the dual to be rhombus-faced parallelopipeds which are quite flattened, compared to most parallelopipeds I have seen before. This polyhedron is isomorphic to the cube, just as the elongated octahedra in the first compound were each isomorphic to the Platonic octahedron. Given that the cube and octahedron are duals, this is no surprise.

Stella 4d may be tried for free, as a trial download, at this website: http://www.software3d.com/Stella.php.
Focus
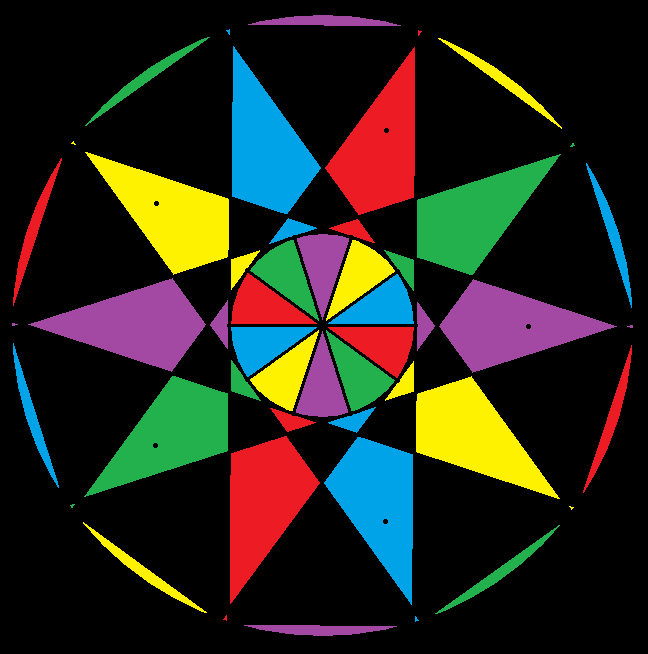
Various Views of Three Different Polyhedral Compounds: Those of (1) Five Cuboctahedra, (2) Five of Its Dual, the Rhombic Dodecahedron, and (3) Ten Components — Five Each, of Both Polyhedra.
Polyhedral compounds differ in the amount of effort needed to understand their internal structure, as well as the way the compounds’ components are assembled, relative to each other. This compound, the compound of five cuboctahedra, and those related to it, offer challenges not offered by all polyhedral compounds, especially those which are well-known.
The image above (made with Stella 4d, as are others in this post — software available here) is colored in the traditional style for compounds: each of the five cuboctahedra is assigned a color of its own. There’s a problem with this, however, and it is related to the triangular faces, due to the fact that these faces appear in coplanar pairs, each from a different component of the compound.
The yellow regions above are from a triangular face of the yellow component, while the blue regions are from a blue triangular face. The equilateral triangle in the center, being part of both the yellow and blue components, must be assigned a “compromise color” — in this case, green. The necessity of such compromise-colors can make understanding the compound by examination of an image more difficult than it with with, say, the compound of five cubes (not shown, but you can see it here, if you wish). Therefore, I decided to look at this another way: coloring each face of the five-cuboctahedra compound by face type, instead of by component.
Another helpful view may be created by simply hiding all the faces, revealing internal structure which was previously obscured.
Since the dual of the cuboctahedron is the rhombic dodecahedron, the dual of the compound above is the compound of five rhombic dodecahedra, shown, first, colored by giving each component a different color.
A problem with this view is that most of what’s “going on” (in the way the compound is assembled) cannot be seen — it’s hidden inside the figure. An option which helped above (with the five-cuboctahedra compound), coloring by face type, is not nearly as helpful here:
Why wasn’t it helpful? Simple: all sixty faces are of the same type. It can be made more attractive by putting Stella 4d into “rainbow color” mode, but I cannot claim that helps with comprehension of the compound.
With this compound, what’s really needed is a “ball-and-stick” model, with the faces hidden to reveal the compound’s inner structure.
Since the two five-part compounds above are duals, they can also be combined to form a ten-part compound: that of five cuboctahedra and five rhombic dodecahedra. In the first image below, each of the ten components is assigned its own color.
In this ten-part compound, the coloring-problem caused in the first image in this post, coplanar and overlapping triangles of different colors, vanishes, for those regions of overlap are hidden in the ten-part compound’s interior. This is one reason why this coloring-scheme is the one I find the most helpful, for this ten-part compound (unlike the two five-part compounds above). However, so that readers may make this choice for themselves, two other versions are shown below, starting with coloring by face type.
Finally, the hollow version of this ten-part compound. This is only a personal opinion, but I do not find this image quite as helpful as was the case with the five-part compounds described above.
Which of these images do you find most illuminating? As always, comments are welcome.
5, 10, and 15 (from 2012)
Another Modest Proposal (with Apologies to Swift)
The day on this planet is 84,600 seconds long. That’s not far from 100,000 — so we could shorten the second a bit, call it something else, and get 100,000 of them each day to create a decimal clock. 100 of these “jiffies” could make a “stretch,” and then 100 “stretches” could make a deciday (the new version of an hour). Ten decidays, of course, make a day, so these neo-hours are pretty long, compared to the hours we’re used to experiencing. This is just practice for making an improved 10-month calendar, of course.
Why go to all this trouble? To get rid of astrology forever, that’s why!
Ten Enneagrams
Image

These enneagrams are of the {9/3} variety, which means each one is made of three concentric, equilateral triangles. One of these enneagrams is at the center; the other nine surround it.
Not “Dead Presidents”
Image

Attention, Americans:
These two men, Alexander Hamilton and Benjamin Franklin, are, indeed, dead. However, neither of them ever served as president. Therefore, please stop calling money “dead presidents,” unless you are excluding these two denominations, and, moreover, please stop this immediately.
Your cooperation is appreciated.