A Radial Tessellation Featuring Regular Octagons, Equilateral Hexagons, and Convex Pentagons
Image
Reply
Tag Archives: radial
A Chiral, Radial Tessellation of Equilateral Triangles, Rhombi, and Isosceles Trapezoids
After that messy, irregular tessellation in the last post, I had to make something which looked better.
A Fractal Tessellation of Golden Triangles, Golden Gnomons, and Regular Decagons
Image
A Radial Tessellation of the Plane Using Squares and 45/135 Degree Rhombi
This is an adjustment and extension of the radial tessellation shown in the most recent post here. I am now confident that this pattern could be extended outward, without limit.
A Radial Octagonal Tessellation of Squares and Rhombi
Image
I believe this can be continued, outward, indefinitely. I also believe it is aperiodic. However, I do not have a proof for either of these conjectures.
Two Versions of Mandalas Centered on Regular Octadecagons
If I've tried this once, I've tried it at least fifty-five times….
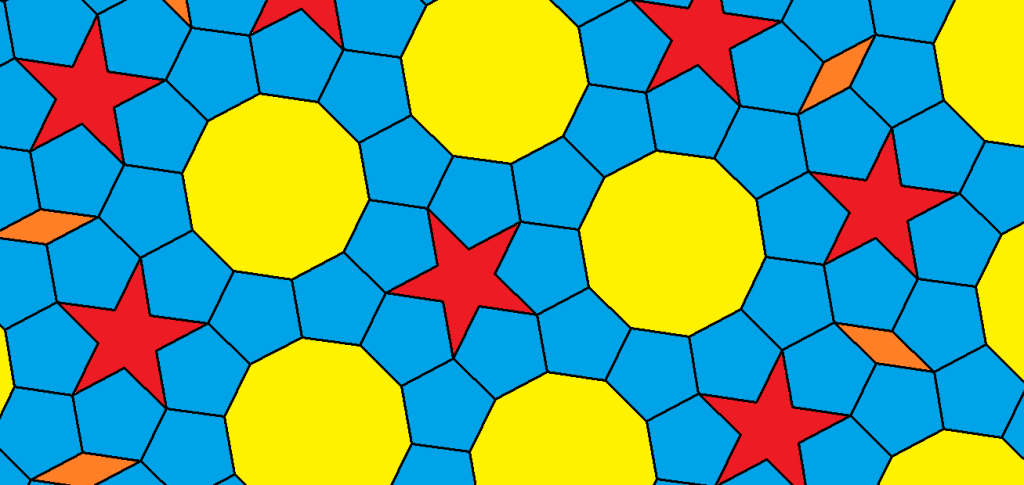
It’s hard to get regular pentagons, regular star pentagons, regular decagons, and related polygons to tessellate the plane while maintaining radial symmetry. This is my latest attempt.
A Radial Tessellation of Regular Pentagons and Rhombi
Image
Radial Five
Image
A Radial Tessellation Using Three Types of Rhombi
The yellow rhombi have angles of 40 and 140 degrees, while the blue rhombi have angles of 80 and 100 degrees, just like in the last post here. However, that post did not include the red rhombi, which have angles of 60 and 120 degrees.
RobertLovesPi.net 