I made this duoprism, a four-dimensional polytope, using Stella 4d. You can try this program for yourself, free, at http://www.software3d.com/Stella.php.
The 5/2, 5/2 Duoprism
Reply
Tag Archives: 4th dimension
The Dodecagonal Duoprism
There are objects in hyperspace known as duoprisms, which have prismatic cells. This one’s cells are 24 dodecagonal prisms. It was made using Stella 4d, available here.
Zome Hyperdodecahedron
This is one projection of the four-dimensional hyperdodecahedron, or 120-cell, rendered in Zome. All the part for this come in a single kit, and, if you want it for yourself, you can find it for sale at this website.
I did have student help with the construction of this, for which I am grateful. However, for legal and ethical reasons, I cannot credit the students by name.
Here’s a closer view, through the “core” of all-blue pentagons:
Zome is a great product. I recommend it strongly, and without reservation (and no, they aren’t paying me anything to write this).
23-Tex: The Truncated 600-Cell
One of the regular 4-dimensional polytopes, or polychora, is called the 600-cell. If you truncate it, you get the figure above, called “23-tex” for short. Its unit cells are 600 truncated tetrahedra, as well as 120 icosahedra. As shown above, you see only the cells, with space between them so you can see them, and vertices and edges rendered invisible. If the vertices and edges are shown, though, 23-tex looks like this:
Since these are four-dimensional figures, it’s not possible to see what these really look like all at once, in hyperspace, because you, the observer, are trapped in a universe where only three spatial dimensions are easy to perceive. That’s one reason I’m showing these figures with them rotating — as they spin, in hyperspace, the “slice” of the shape which appears as a three-dimensional projection, in our universe, changes. Over time, then, you get to see it all — but, in hyperspace, its appearance would be different. If you try to imagine a living creature living inside a horizontal Euclidean plane, and this creature trying to picture a three-dimensional shape, that can help with understanding the nature of the problem that arises when three-dimensional beings try to picture anything involving a fourth spatial dimension.
Three-dimensional polyhedra can be unfolded, and shown as flat “nets” made out of polygons. Well, what does the “net” of a four-dimensional polytope look like? The answer is one dimension “down” from four: the net is a bunch of three-dimensional polyhedra, stuck together at their faces, just as the nets of polyhedra are made of polygons joined at their edges. Here’s one possible net for 23-tex:
The three images above were produced using Stella 4d: Polyhedron Navigator, software you may try for yourself, here.
Four Views of a Tesseract, Rotating in Hyperspace
Image
These tesseract views are all of the perspective projection-type, with the first one, above, being done in cell-first fashion.
The next one is projected edge-first.
The third one is projected vertex-first.
Lastly, face-first:
Although all of these are rotating in the same direction in hyperspace, the different projection-choices make the second and fourth images appear to be rotating in different directions. Why? I’m still trying to figure that out!
These animations were created with Stella 4d, software available at www.software3d.com/Stella.php.
20-Thex: A Four-Dimensional Polytope
Image
In hyperspace, or four-space, there are six regular polychora, analogous to the Platonic Solids in three-space. Beyond the Platonics in the study of polyhedra comes, of course, the Archimedean Solids, which include many truncated forms of Platonic polyhedra.
In hyperspace, there are varieties of progressively-less regular polychora, also, and one of these, in a group called the truncates, is called 20-thex, or simply the “thex.” (Those are short names for this polychoron; it’s also called the truncated hexadecachoron, or truncated 16-cell.) What you see above is a (seemingly) three-dimensional projection of a thex, as it rotates in hyperspace.
Just as polyhedra have polygons as faces, polychora have polyhedra as unit cells. This is the net for the thex. As you can see, the thex is composed of both truncated tetrahedra and octahedra.
Both of these images were created using Stella 4d, which you can try for yourself at http://www.software3d.com/Stella.php.
Another View of the 600-Cell
Image
Not long ago, I posted one rotating projection of the regular polytope known as the 600-cell. Here is another.
Software used: see http://www.software3d.com/stella.php.
The Hyperspace Analogue of the Stella Octangula
The simplest polyhedron is the tetrahedron, and it is self-dual. The compound of two tetrahedra puts these duals together, and is most often called the Stella Octangula, a name Johannes Kepler gave it in the early 17th Century.
In hyperspace, or 4-space, the simplest polychoron is the pentachoron, or 5-cell. Like the tetrahedron in 3-space, it is also self-dual. Here is the compound of two of them: hyperspace’s version of the Stella Octangula.
Website to find the software used to make these images: www.software3d.com/stella.php
Rotating Compound of the Tesseract and Its Dual
Image
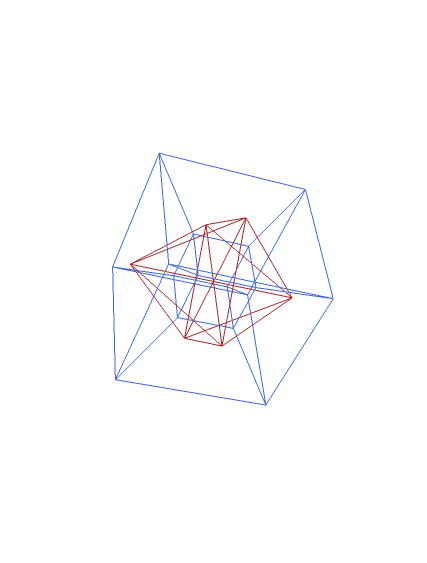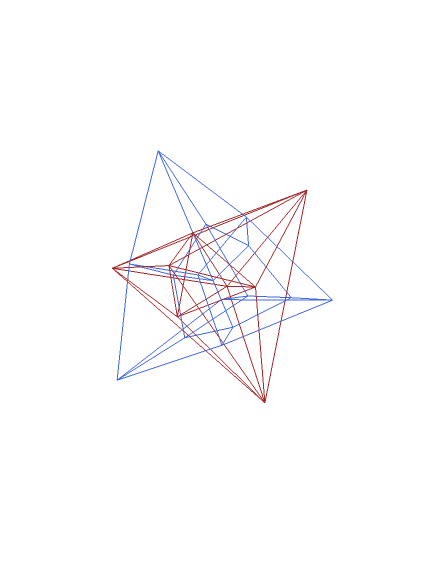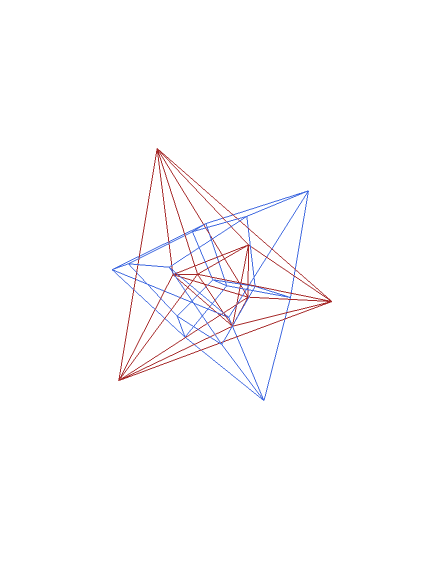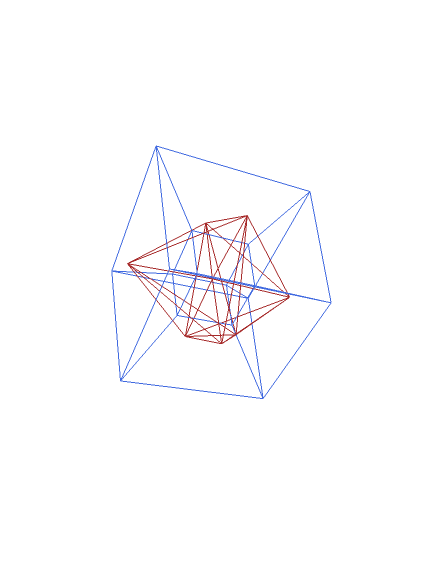
Blue figure: a projection of the tesseract, or hypercube; also known as the 8-cell or octachoron — a four-dimensional figure composed of eight cubic cells in a regular arrangement.
Red figure: its dual, the 16-cell or hexadecachoron, which is composed of sixteen tetrahedral cells.
To buy (or just try) the software used to make this image, Stella 4d, please visit http://www.software3d.com/Stella.php.
The Two Simplest Polychora
The most familiar polychoron, to those who have heard of any of them, is the hypercube, or tesseract. It is analogous to the cube, but in four dimensions. All polychora are four-dimensional. With numbers of spatial dimensions above four, only the term “polytope” is used. Polyhedra are 3-polytopes, and polychora are 4-polytopes.
This is a three-dimensional projection of a tesseract, as it rotates in hyperspace, casting a “shadow” into our space:
In three dimensions, a cube is not the simplest polyhedron. A tetrahedron (a regular triangle-based pyramid) is simpler.
The simplest polychoron is composed of five tetrahedral cells, and is analogous to the tetrahedron, but in hyperspace. Here is a rotating “hypertetrahedron.”
There are even more names for these two polychora, based on the number of cells (cubes or tetrahedra). The tesseract/hypercube is composed of eight cubes, so it is called the 8-cell, as well as the octachoron. The preferred names for the hypertetrahedron are the 5-cell and the pentachoron, as it is composed of five (tetrahedral) cells.
Just as there are other Platonic solids not mentioned here, there are other regular polychora as well. The others will be subjects of upcoming posts, and one has already appeared here once (the 120-cell, or hyperdodecahedron), just three posts back.
Software note: these .gifs were made using Stella 4d, which may be purchased, and/or tried for free (on a trial basis), at http://www.software3d.com/Stella.php.
RobertLovesPi.net 