Mathematicians have discovered more than one set of rules for polyhedral stellation. The software I use for rapidly manipulating polyhedra (Stella 4d, available here, including as a free trial download) lets the user choose between different sets of stellation criteria, but I generally favor what are called the “fully supported” stellation rules.

For this exercise, I still used the fully supported stellation rules, but set Stella to view these polyhedra as having only tetrahedral symmetry, rather than icosidodecahedral (or “icosahedral”) symmetry. For the icosahedron, this tetrahedral symmetry can be seen in this coloring-pattern.

The next image shows what the icosahedron looks like after a single stellation, when performed through the “lens” of tetrahedral symmetry. This stellation extends the red triangles as kites, and hides the yellow triangles from view in the process.

The second such stellation produces this polyhedron — a pyritohedral dodecahedron — by further-extending the red faces, and obscuring the blue triangles in the process.

The third tetrahedral stellation of the icosahedron produces another pyritohedral figure, which further demonstrates that pyritohedral symmetry is related to both icosidodecahedral and tetrahedral symmetry.

The fourth such stellation produces a Platonic octahedron, but one where the coloring-scheme makes it plain that Stella is still viewing this figure as having tetrahedral symmetry. Given that the octahedron itself has cuboctahedral (or “octahedral”) symmetry, this is an increase in the number of polyhedral symmetry-types which have appeared, so far, in this brief survey.

Next, I looked at the fifth tetrahedral stellation of the icosahedron, and was surprised at what I found.

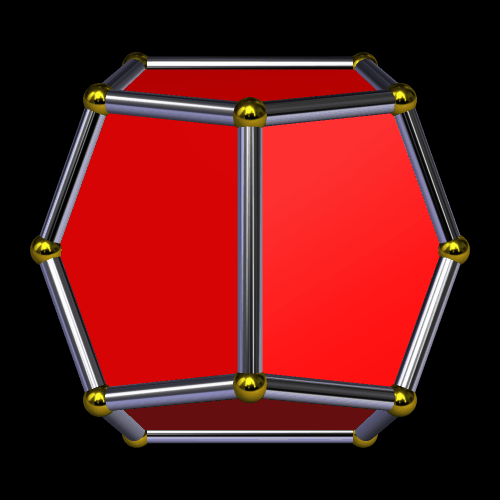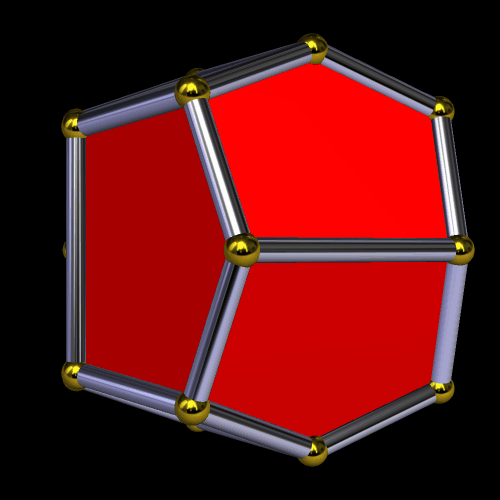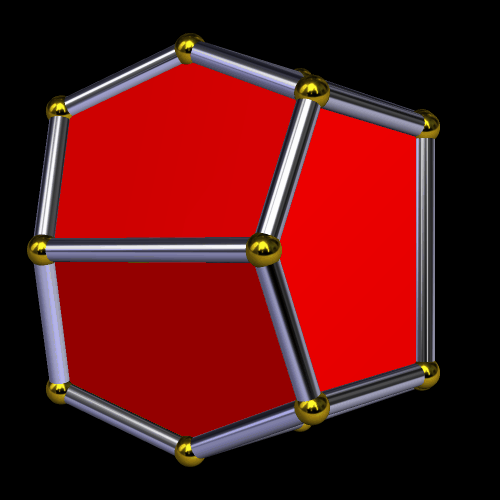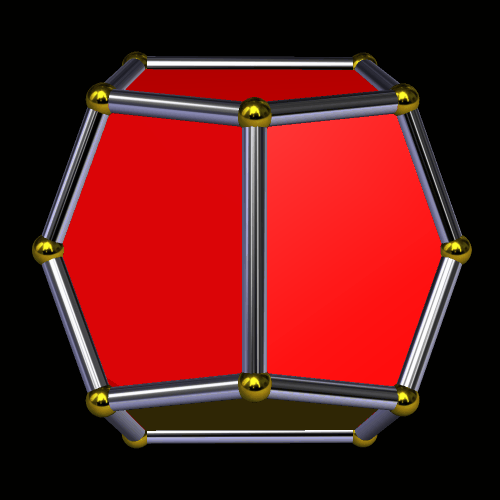
While I was curious about what would happen if I continued stellating this polyhedron, I also wanted to see this fifth stellation’s convex hull, since I could already tell it would have only hexagons and triangles as faces. Here is that convex hull:

For the last step in this survey, I performed one more tetrahedral stellation, this time on the convex hull I had just produced.