As you can see, these circles intersect on the sides of the triangles. I did not expect that, nor have I proven it. I have moved the triangle around to check to see if this remained true, and it did pass this test. If I can figure out a proof for this, I’ll post it; if one exists already, please post a comment letting me know where to find it.
Later edit: I found out that these points of intersection are the altitude feet. Here’s a diagram showing the lines containing the altitudes, meeting at the orthocenter. These blue lines also contain the angle bisectors of the brown triangle defined by the altitude feet.





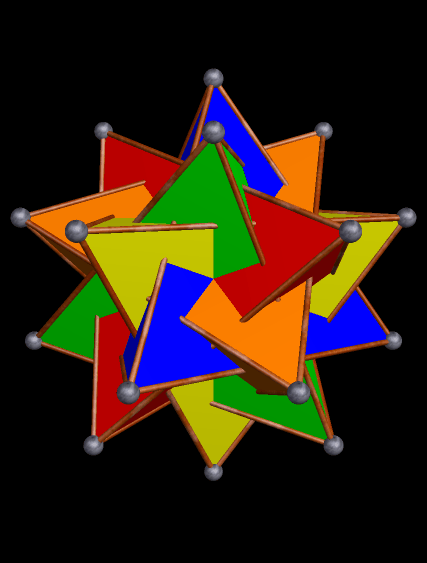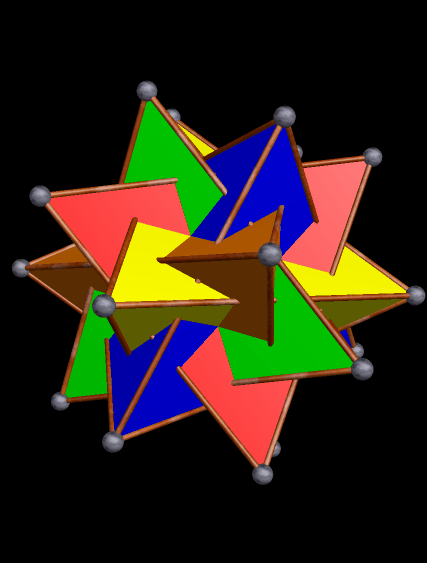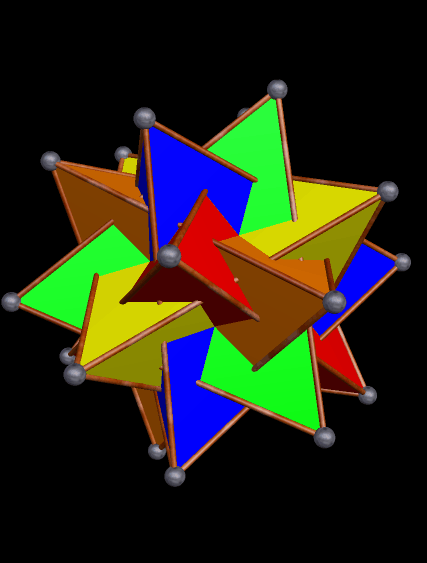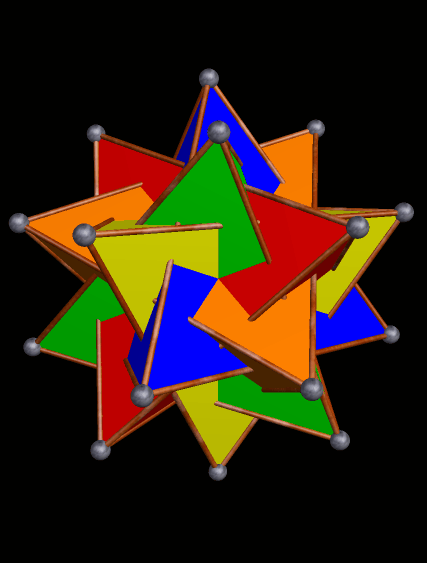 What would happen if each face in this compound were to be augmented by an octahedron of the same color? To find out, just see the next post!
What would happen if each face in this compound were to be augmented by an octahedron of the same color? To find out, just see the next post!