So far as I know, no one knows how many otherwise-regular convex “bowtie” polyhedra exist — that is, convex polyhedra whose only faces are regular polygons, and pairs of isosceles trapezoids in “bowtie” formation. With the aid of software called Stella 4d, which you can find at http://www.software3d.com/Stella.php, I do believe I’ve found another one which hasn’t been seen before.

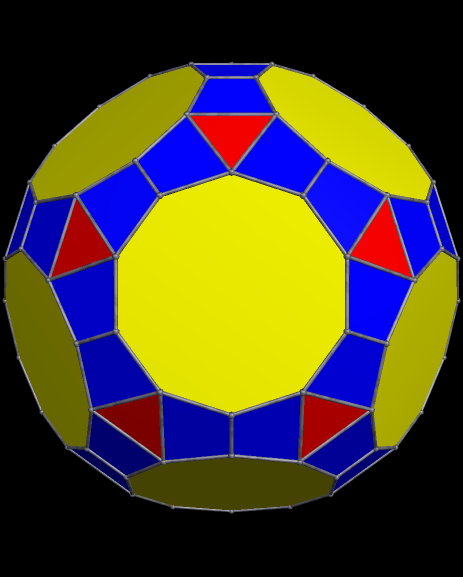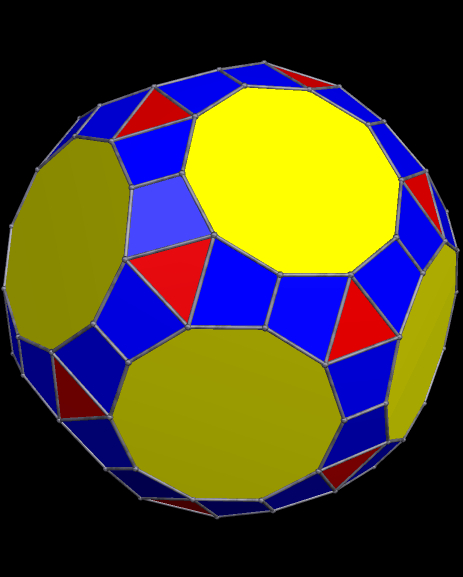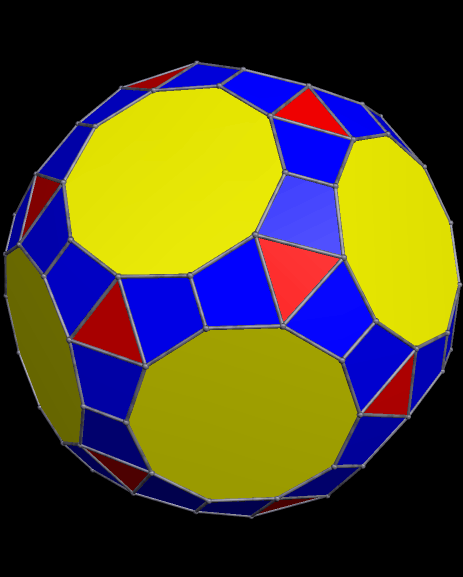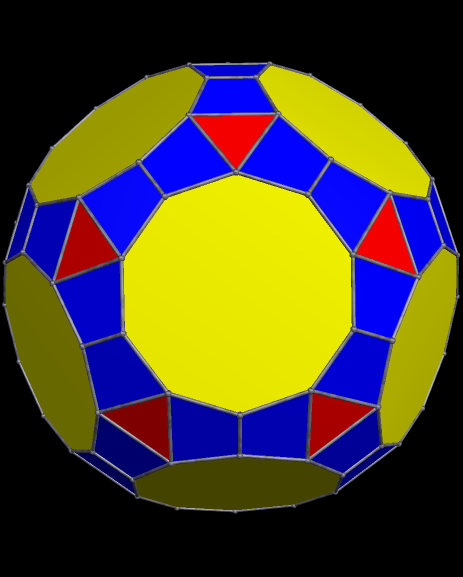
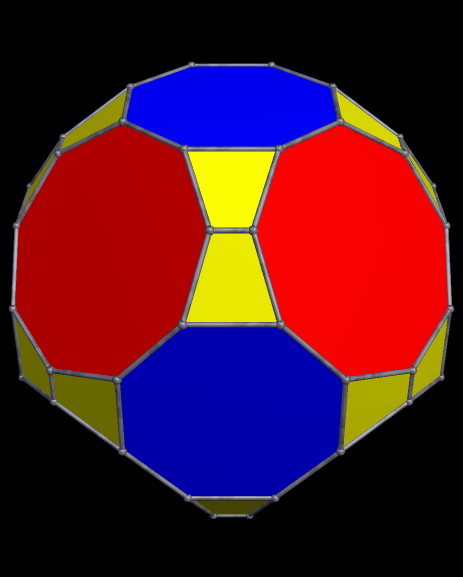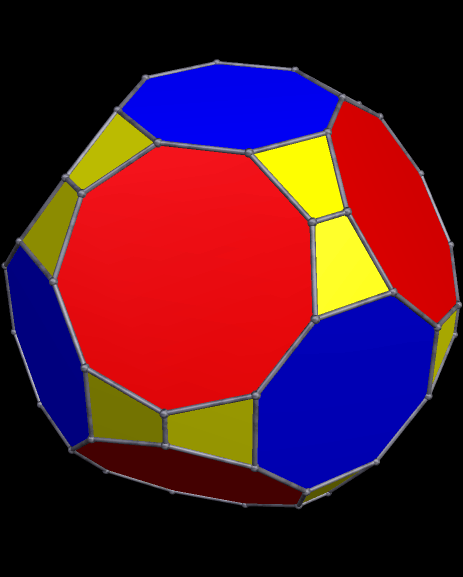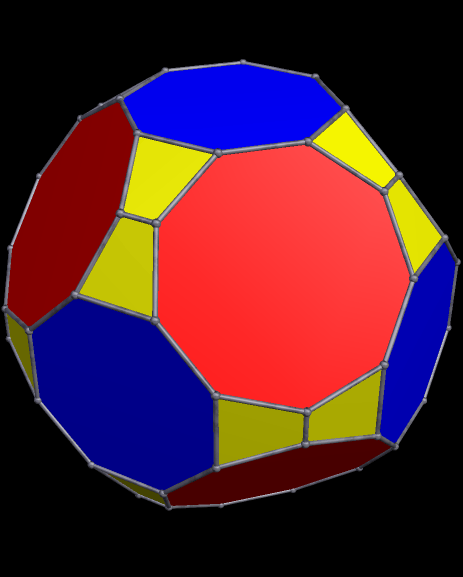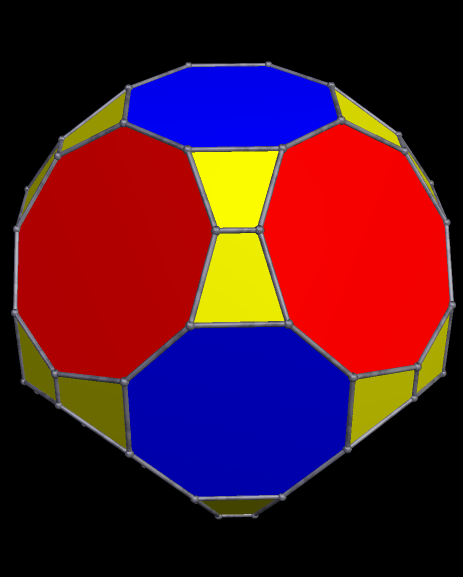
To make it, I started with what is probably the most well-known near-miss to the Johnson Solids, this polyhedron featuring enneagons (nine-sided polygons; also called “nonagons”):

I then augmented each enneagonal face with regular antiprisms, took the convex hull of the result, and then used Stella’s “try to make faces regular” function — and it worked, making the octagons regular, as well as the enneagons.

Update:  It turns out that this polyhedron has been seen before.  It’s at http://www.cgl.uwaterloo.ca/~csk/projects/symmetrohedra/ — and there are even more at http://www.cgl.uwaterloo.ca/~csk/papers/kaplan_hart_bridges2001.pdf. These include several more “bowtie” polyhedra found among what those researchers, Craig S. Kaplan and George W. Hart, call “symmetrohedra.” They call this particular polyhedron a “bowtie octahedron.”