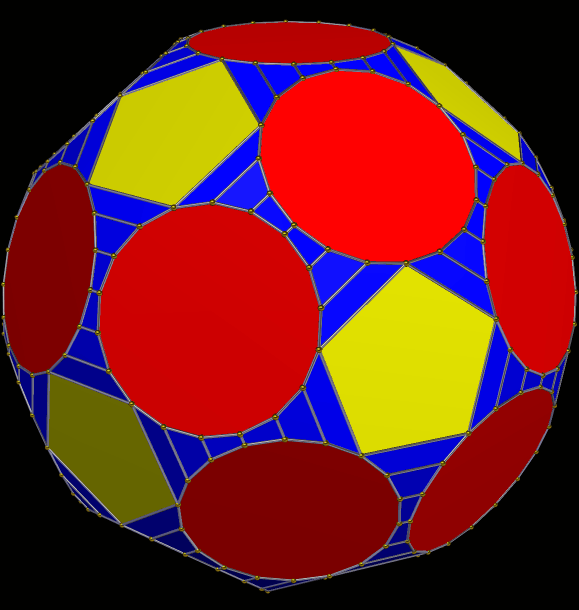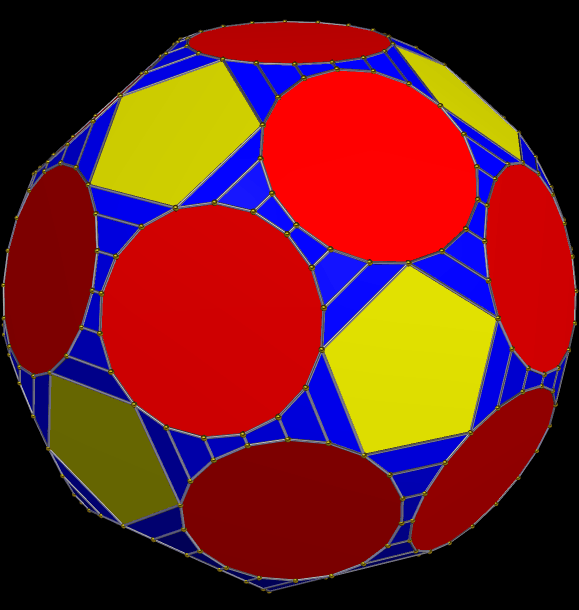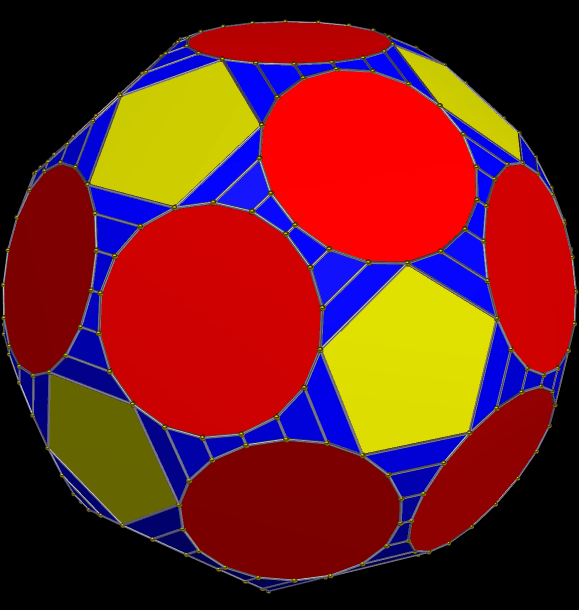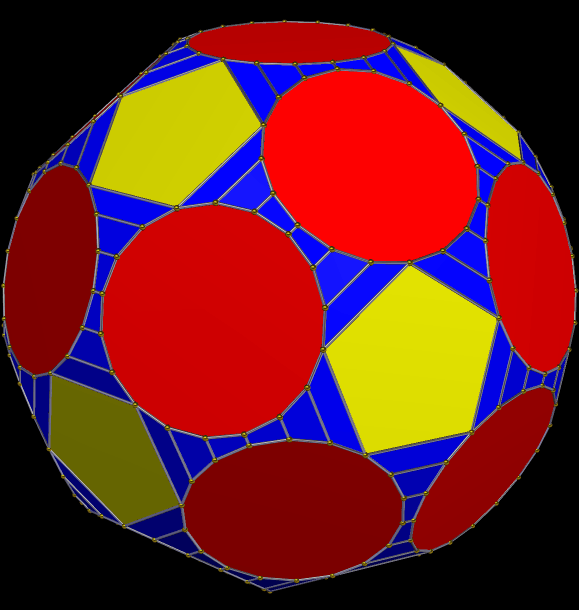
In the last post here, I displayed a chiral symmetrohedron derived from the snub dodecahedron, and today I am presenting its “little brother,” which is derived from the snub cube. Both models were created using the “morph duals by truncation” function of Stella 4d: Polyhedron Navigator, a program you can download and try, for free, at this website. This newer solid contains six squares, 32 equilateral triangles, and 24 irregular pentagons, for a total of 62 faces.
A Chiral Symmetrohedron
This symmetrohedron was derived from the snub dodecahedron. It contains twelve regular pentagons and sixty irregular pentagons, as well as eighty equilateral triangles, for a total of 152 faces. I made it using Stella 4d (with the “morph duals by truncation” function), a program you can download and try, for free, at this website.
A Polyhedron Derived From the Great Rhombicosidodecahedron
I made this using Stella 4d, which you can try for yourself right here.
Four Polyhedra Derived From the Icosidodecahedron
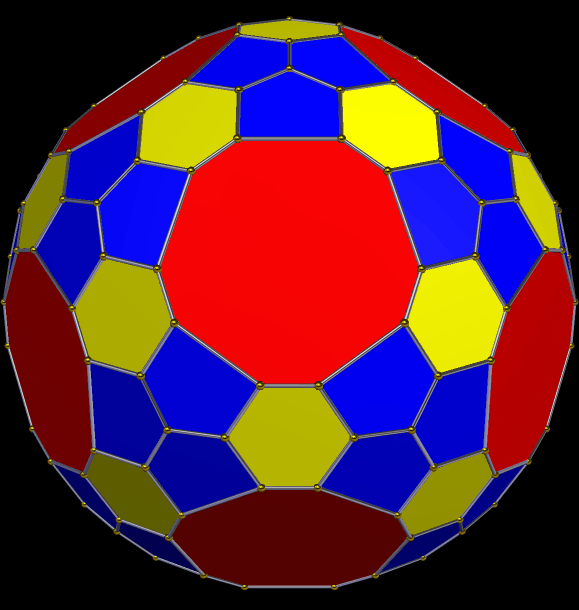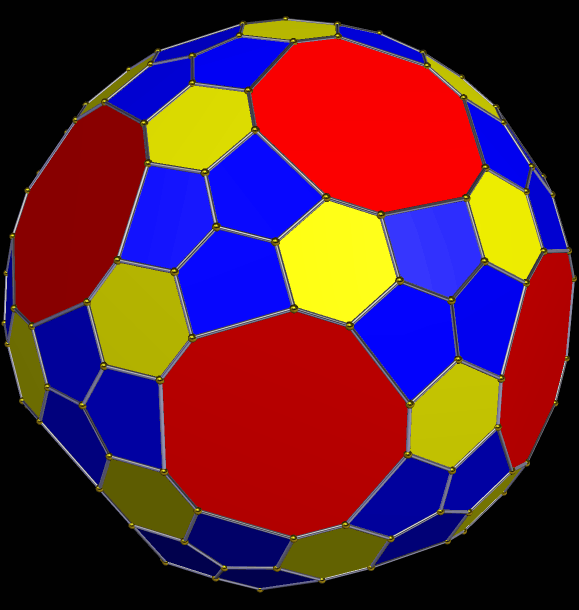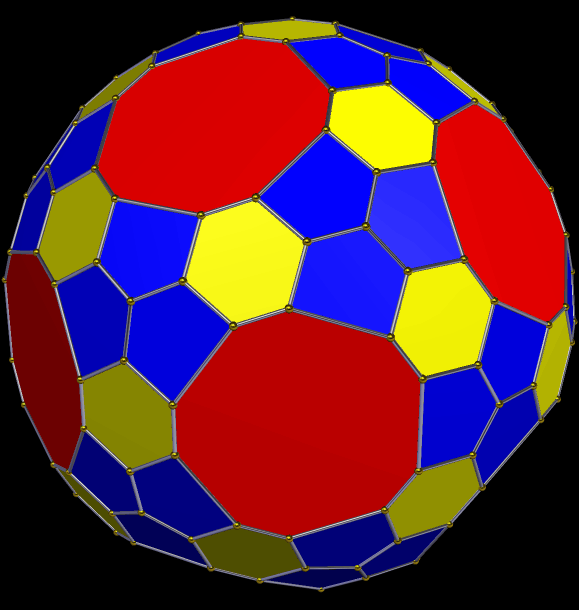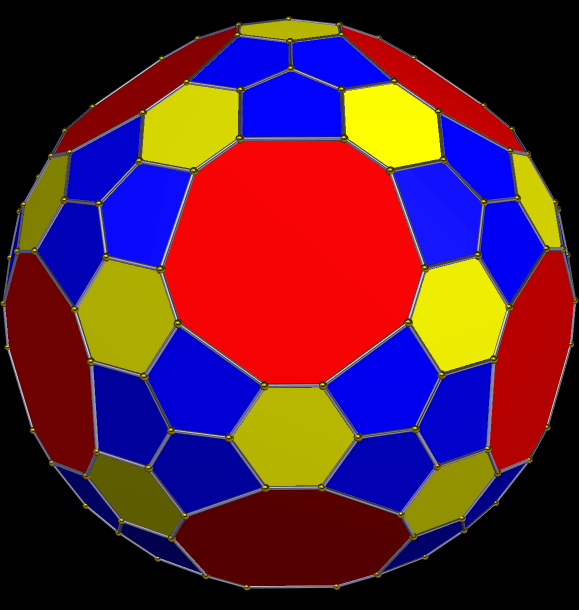
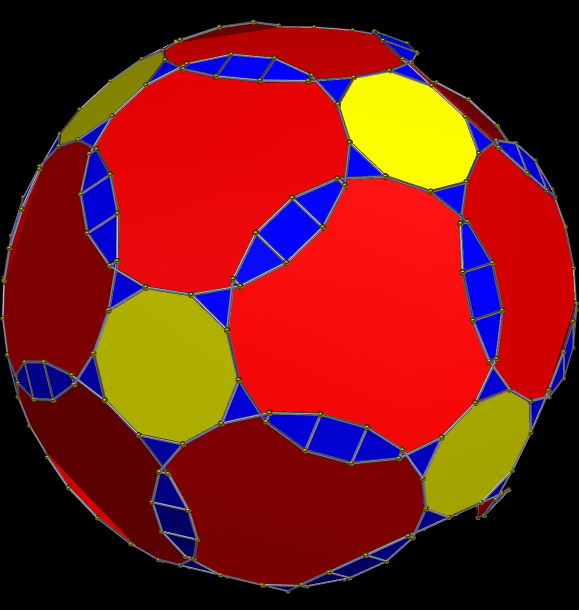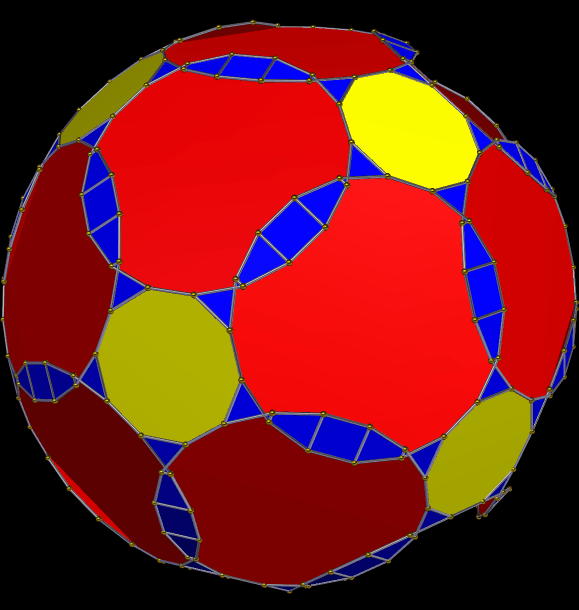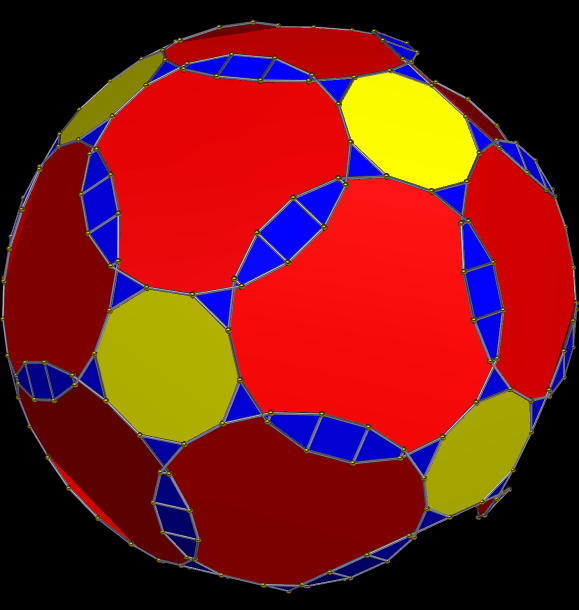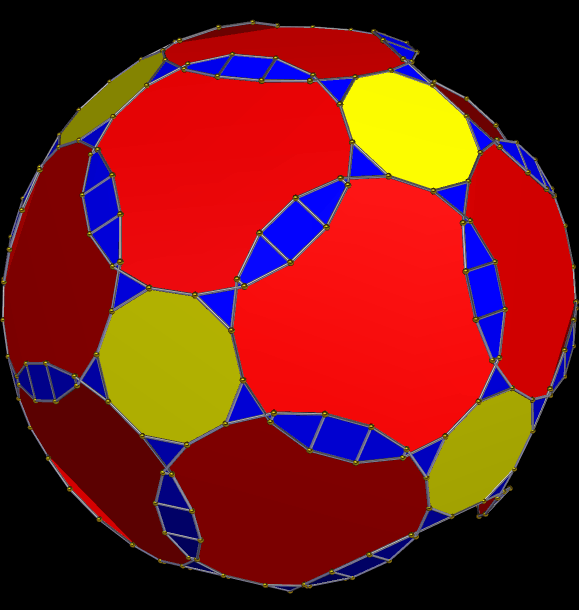
A Symmetrohedron Derived From the Great Rhombicosidodecahedron
This solid has all the faces of the great rhombicosidodecahedron, plus 120 scalene triangles. I made it using Stella 4d, which you can try for free right here.
Kepler’s “Stella Octangula,” With Ten Variants
Here’s Johonnes Kepler’s Stella Octangula — also known as the compound of two tetrahedra.
What follows are ten variants of this solid, all made using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.


A 90-Faced Polyhedron
This polyhedron has sixty kite faces and thirty octagonal faces. I made it using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
A Polyhedron Featuring Twenty Regular Octadecagons and Twelve Regular Decagons
I made this using Stella 4d, which you can try for free right here.
Regular Octadecagons As Faces of Symmetrohedra
I tried to make a symmetrohedron using regular octadecagons and regular decagons, but that combination forces the octadecagons to overlap, and that causes the would-be symmetrohedron to be non-convex.
I tried to augment these octadecagons with antiprisms, and then form the convex hull of the result. Here’s what I found:
I made these using Stella 4d, which you can try for free right here.
A Face-Based Zonohedrified Rhombic Enneacontahedron
The decagons and octagons in this zonohedron are regular. The octadecagons are, sadly, only equilateral. I made this using Stella 4d, which you can try for free, right here.