The 152 faces of this symmetrohedron include twelve regular decagons, twenty regular hexagons, and 120 irregular quadrilaterals arranged in thirty groups of four quads each. I made it using Stella 4d, which you can download here as a free trial version.
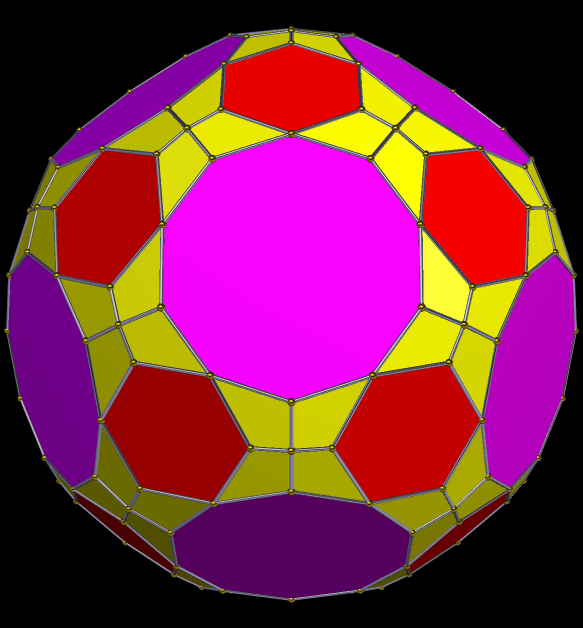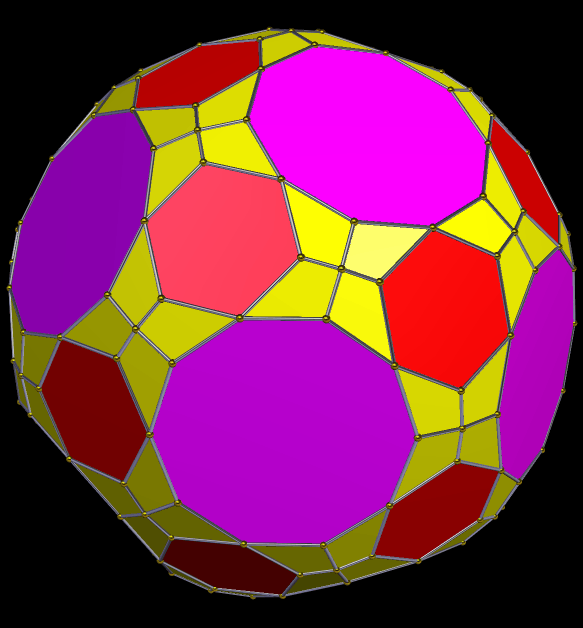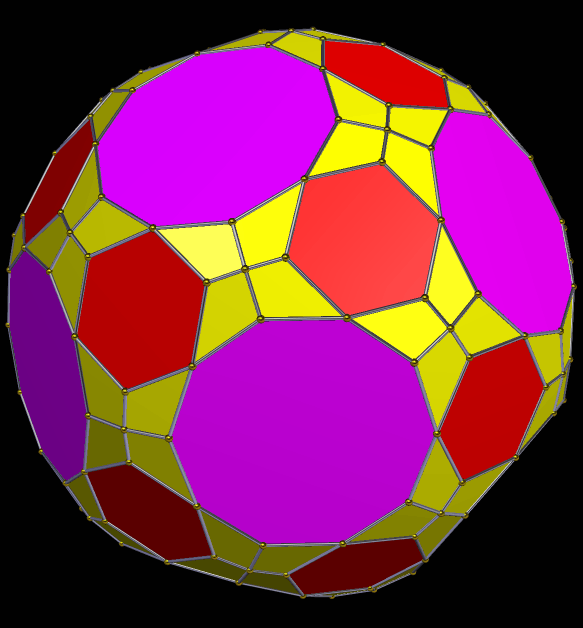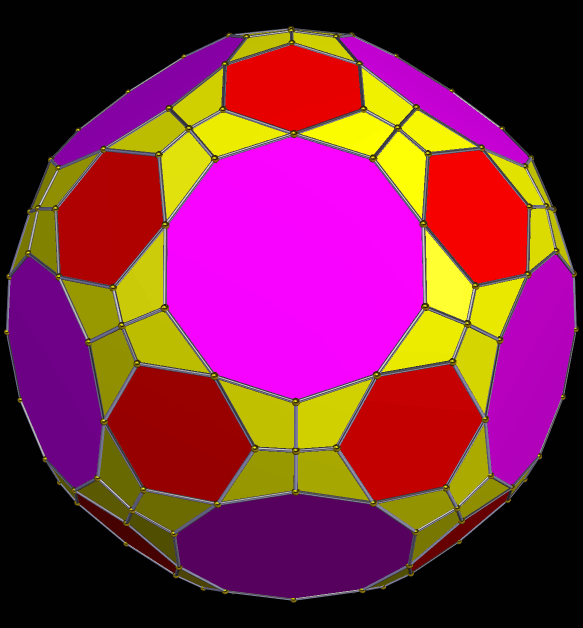
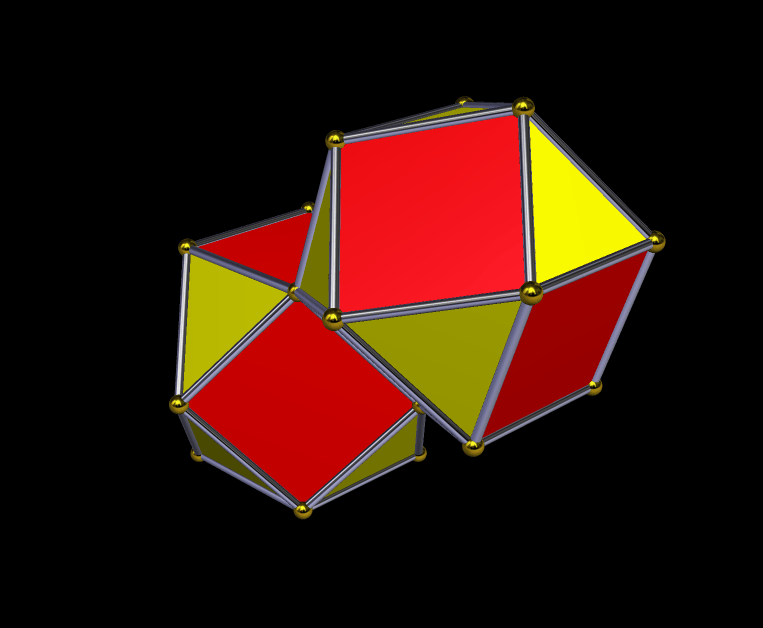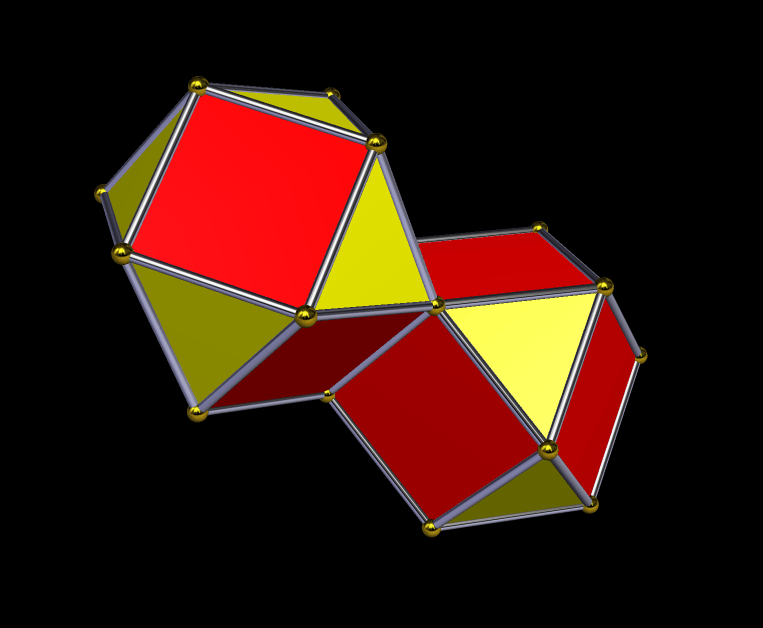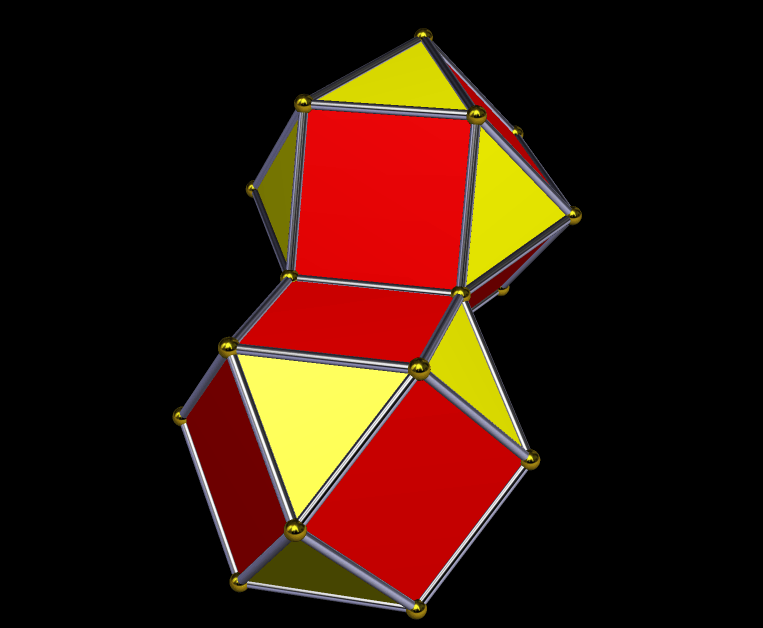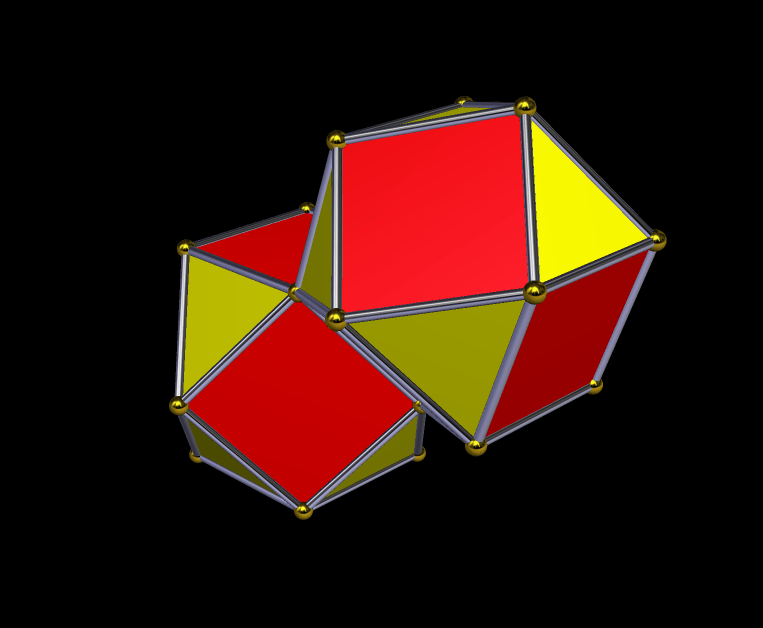
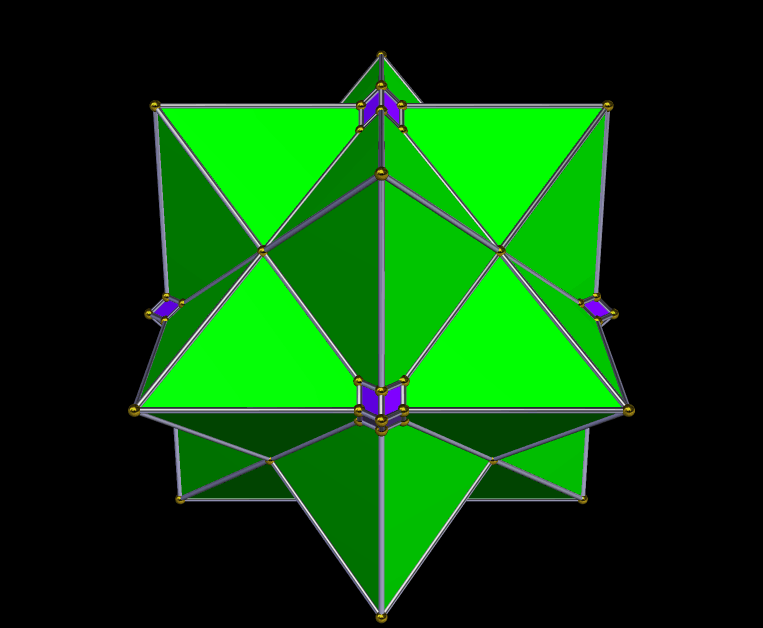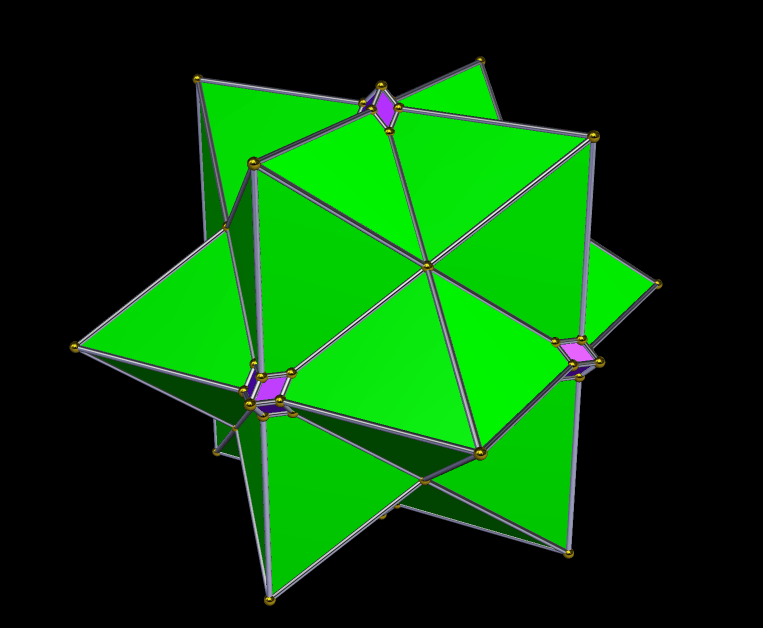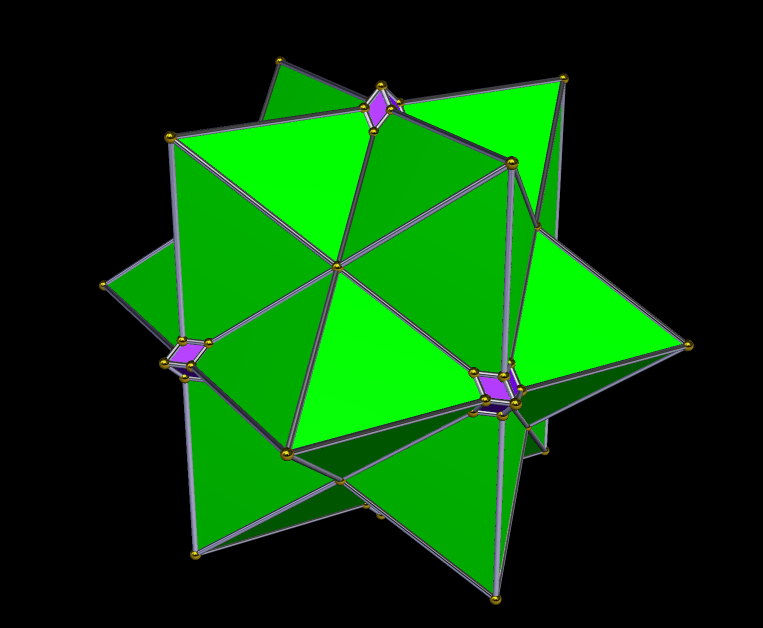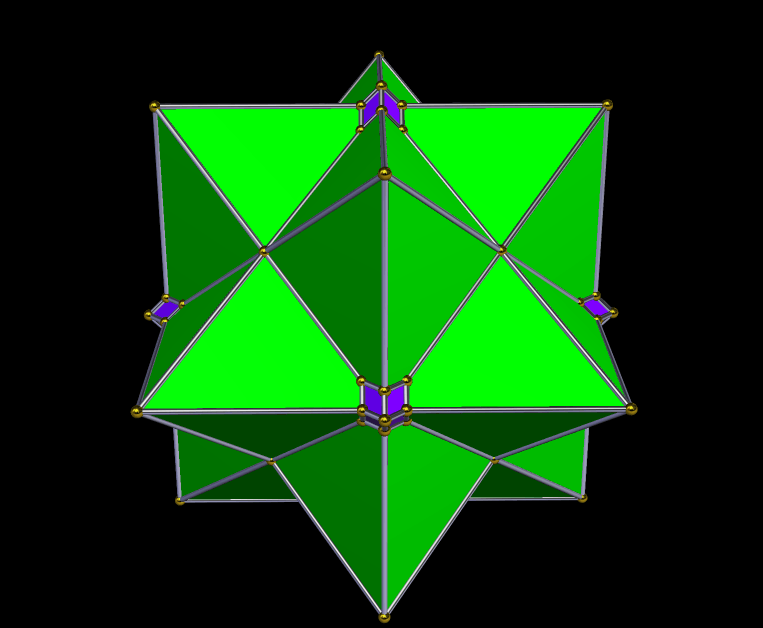
The second stellation of the dysdyakis triacontahedron, seen above, is an interesting two-part polyhedral compound. The dysdyakis triacontahedron is one of the Catalan solids, and is the dual of the great rhombicosidodecahedron.
There’s also a “little brother” to this first compound — it’s the second stellation of the dysdyakis dodecahedron, which is the dual of the great rhombicuboctahedron. Like its “big brother,” it’s a two-part compound. It is shown below.
Interestingly, the components of these two compounds are “stretched” versions of two other Catalan solids: the pentagonal hexecontahedron (dual of the snub dodecahedron), and the pentagonal icositetrahedron (dual of the snub cube).
I made these virtual models using Stella 4d, which you can download and try for free at http://www.software3d.com/Stella.php.
The Catalan Solids shown here are the dysdyakis dodecahedron (dual of the great rhombicuboctahedron) and the dysdyakis triacontahedron (dual of the great rhombicosidodecahedron). In each one, all the faces are scalene triangles, and half of them have been rendered invisible, so that you can see the inside view of faces on the far side of each polyhedron. The remaining faces are shown in “rainbow color mode.”
I made these polyhedron models using Stella 4d, which you can try for free right here.
There are at least two ways to make a double cuboctahedron. One way is to join two cuboctahedra at a square face.
The dual of a single cuboctahedron is a rhombic dodecahedron. The dual of this first double cuboctahedron, however, doesn’t look like a rhombic dodecahedron at all.
Another way to make a double cuboctahedron is to join two cuboctahedra at a triangular face.
Here’s the dual of the second type of double cuboctahedron.
I created these four polyhedra using Stella 4d, a program you can download and try for free, as a trial version, at this website.
I made this using Stella 4d, a program you can try for free at this website.
These compounds differ in the relative sizes of their components. I made all three using Stella 4d, which you can try for free right here.
I made these using Stella 4d: Polyhedron Navigator. You can give this software a try, right here, for free.
I stumbled across this compound the other day, while playing around with Stella 4d: Polyhedron Navigator (available here).
At first, I thought this was a compound of six tetrahedra, but careful examination reveals that the tetrahedra are missing parts along the middle of some of their edges. I looked up the canonical compound of six tetrahedra in Stella‘s library, and here it is. As you can see, it’s quite similar — but it does have those “missing” pieces added.
I stumbled across this while playing around with my favorite polyhedron-manipulation tool, Stella 4d. You can try this program for free at http://www.software3d.com/Stella.php.
RobertLovesPi.net 