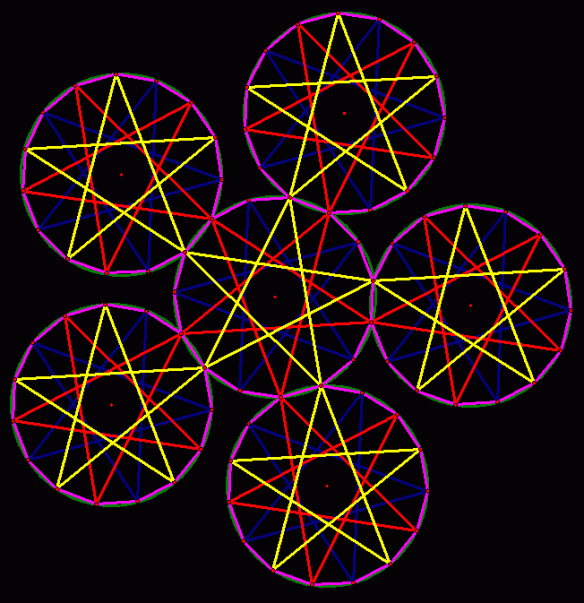
Another accidental discovery made while manipulating polyhedra with Stella 4d, which you can try for free at http://www.software3d.com/stella.php.
Sixty Irregular Pentagons in a Regular Pattern
Image
Reply
Monthly Archives: October 2013
Polyhedron Featuring Nonagons and Rhombi
Image
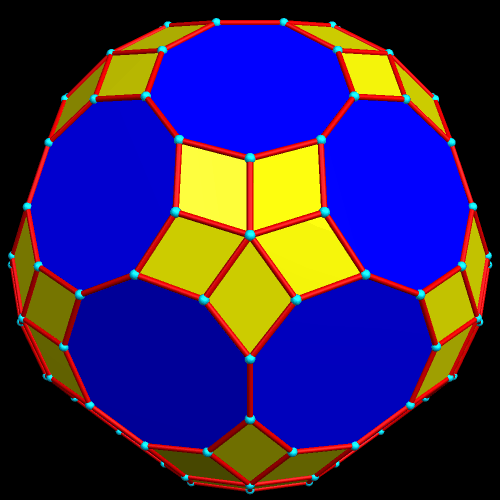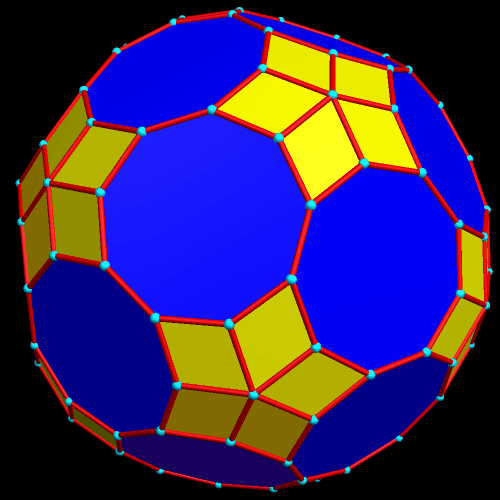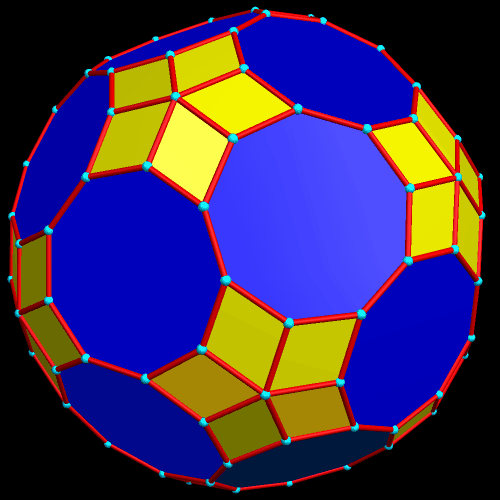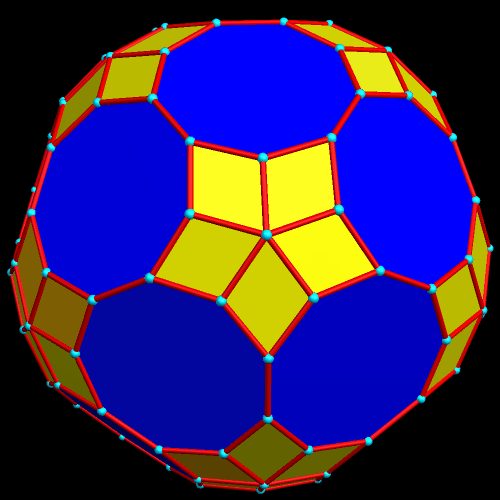
I stumbled across this while manipulating polyhedra with Stella 4d, which you can try for free at http://www.software3d.com/stella.php.
I don’t think the nonagons are quite regular, and the yellow figures may be near-rhomboidal kites, rather than true rhombi. Nevertheless, I find it an interesting figure, and am posting it here so I can find it for further investigations later.
Progress
As the people in my life (even in its periphery) get to know me better, I’m finding it necessary less and less often to point out that I’m an atheist, for I’m not running into the assumption-of-Christianity much any more.
On a related note, I also don’t ever have to tell anyone that I don’t collect stamps.
What I do not know: is this a widespread phenomenon, or is it just me who is experiencing it?
Icosahedral Shell
Image
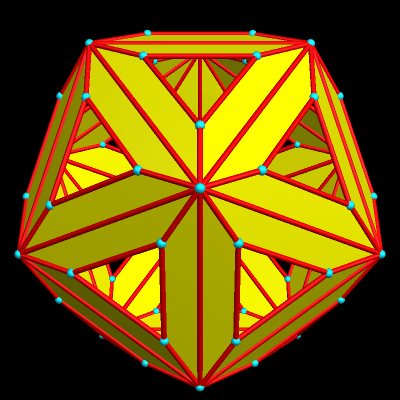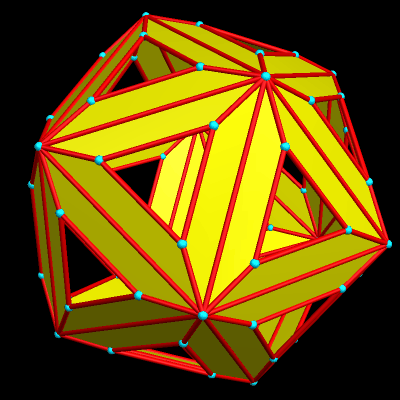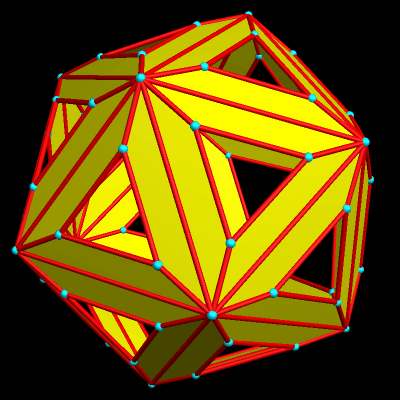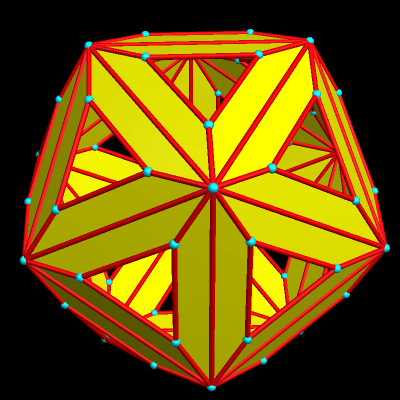
This was created with Stella 4d, software you can try for free at http://www.software3d.com/stella.php.
A “Bowtie” Variant of the Truncated Icosahedron
Image
This has the twelve regular pentagons and twenty regular hexagons of a truncated icosahedron (most familiar to the world as the shape upon which most soccer balls are based), but also has pairs of trapezoids in “bowtie” configurations. I discovered this polyhedron using Stella 4d, which you can try for free at http://www.software3d.com/stella.php.
The 27-63-90 Triangle
Image
I’m not as pleased about finding this special right triangle as I was with the previous ones. For one thing, I didn’t use a regular polygon to derive it, but instead used the 36-54-90 triangle I had previously found, and applied a half-angle trigonometric identity to find the tangent of 27 degrees, as the tangent of half of 54 degrees. According to this identity, tan(27⁰) = (1 – cos(54⁰))/sin(54⁰). Once this gave me the leg lengths, I simply used the Pythagorean Theorem to determine the length of the hypotenuse. Finally, I checked all of this using decimal approximations.
The triple-nested radical in the expression for the hypotenuse is no cause for celebration, either. If anyone knows of a way to put this in simpler exact terms, please let me know.
The 15-75-90 Triangle
Image
As the 30-60-90 triangle is based on an equilateral triangle, the 45-45-90 triangle is based on a square, the 18-72-90 and 36-54-90 triangles are based on the regular pentagon (see https://robertlovespi.wordpress.com/2013/03/12/the-18-72-90-and-36-54-90-triangles/), and the 22.5-67.5-90 triangle is based on the regular octagon (see previous post), so the 15-75-90 triangle is based on the regular dodecagon, shown here with three radii (red) and a single diagonal (purple). The 15-75-90 triangle is shown in yellow. An argument from symmetry is sufficient to show that angle EFC is the right triangle in this triangle, and the larger of its two acute angles (angle FCE) is one-half of an interior angle of this dodecagon. The interior angle of a regular decagon measures 150 degrees (the proof of this is trivial), and so angle FCE must measure half that amount, or 75 degrees. This leaves 15 degrees for angle CEF, via the triangle sum theorem.
What about the side lengths of the 15-75-90 triangle, though? First, consider the red diagonals shown, and let them each have a length of 2. Angles DAF and FAE each measure 30 degrees, since 360/12 = 30, and they are central angles between adjacent radii. This makes angle DAE 60 degrees by angle addition, and triangle DAE is known to be isosceles, since the two red sides are radii of the same regular dodecagon, and therefore are congruent. By the isosceles triangle theorem and triangle sum theorem, then, angles ADE and AED each also measure (180-60)/2 = 60 degrees, so triangle ADE is therefore equilateral, with the purple side, DE, also having a length of two. Symmetry is sufficient to see that DE is bisected by radius AC, which leads to the conclusion that EF, the long leg of the 15-75-90 triangle, has a length of 1.
Segment AF is a median, and therefore also an altitude, of equilateral triangle ADE, and splits it into two 30-60-90 triangles, one of which is triangle AEF. Its hypotenuse, AE, is already known to have a length of 2, while its short leg, EF, is already known to have a length of 1. Segment AF is therefore the long leg of this 30-60-90 triangle, with a length of √3.
AF, length √3, and FC, the short leg of the 15-75-90 triangle, together form dodecagon radius AC, already set at length 2. By length subtraction, then, FC, the 15-75-90 triangle’s short leg, has a length of 2 – √3. A test is prudent at this point, by taking the tangent of the 15 degree angle FEC in the yellow triangle. Tan(15 degrees) is equal to 0.26794919…, which is also the decimal approximation for FC/EF, or (2 – √3)/1.
All that remains to know the length ratios for the sides of the 15-75-90 triangle is to determine the length of EC, its hypotenuse, via the Pythagorean Theorem. The square of length EC must equal the square of 1 plus the square of (2 – √3), so EC, squared, equals 1 + 4 – 4√3 + 3, or 8 – 4√3. The hypotenuse (EC) must therefore be the square root of 8 – 4√3, which is √(8-4√3)) = 2√(2-√3)).
The short leg:long leg:hypotenuse ratio in a 15-75-90 triangle is, therefore, (2-√3):1:2√(2-√3)).
The 22.5-67.5-90 Triangle
Image
In the diagram above, a regular octagon is shown nested inside square LMNP. The central angles of this octagon, such as angle HAF, each measure 360/8 = 45 degrees. Segments HA and FA are radii, and G is the midpoint of HF, making GF a half-side and GA an apothem. Since this apothem bisects angle HAF, angle GAF is 22.5 degrees, making the yellow triangle a 22.5-67.5-90 triangle.
Let FH = 2, as well as FK (and the other six sides of the regular octagon, as well), and GF would then equal 1, since G is the midpoint of FH. Triangle KNF is a 45-45-90 triangle with hypotenuse length 2, giving it a leg length of 2/√2, or simply √2. This makes segment XN (with X the midpoint of EK) have a length of 1 + √2, and the light blue segment, AG, has this same length of 1 + √2, by horizontal translation to the left.
The hypotenuse of the yellow 22.5-67.5-90 triangle can then be found using the Pythagorean theorem, since it is is known that the short leg (GF) has a length of 1, while the long leg (AG) has a length of 1+√2. Let this hypotenuse (AF, shown in red) be x, and then x2 = 12 + (1 + √2)2 = 1 + 1 + 2√2 + 2 = 4 + 2√2, so x, and therefore the hypotenuse, has a length of √(4+2√2).
The 22.5-67.5-90 triangle, therefore, has a short leg:long leg:hypotenuse ratio of 1:1+√2:√(4+2√2).
Starry Icosidodecahedron
Image
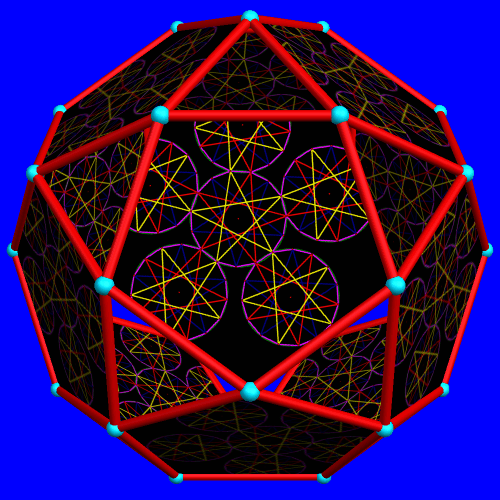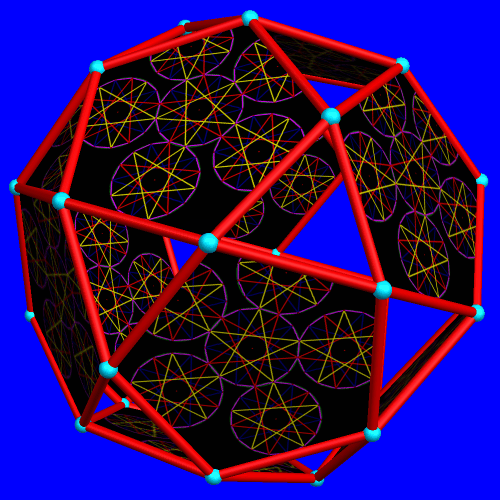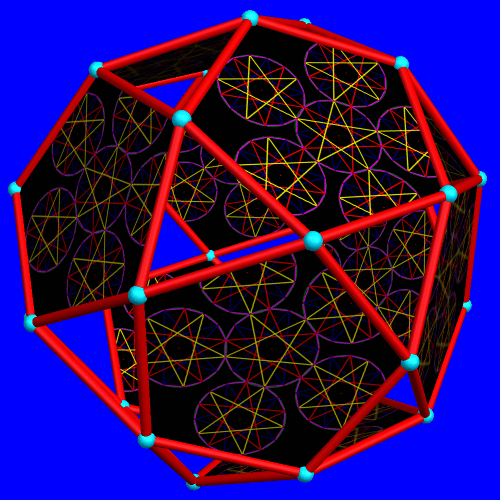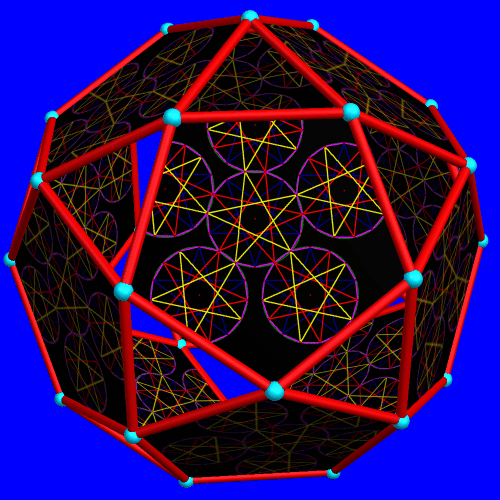
This was created using Geometer’s Sketchpad, MS-Paint, and Stella 4d.
If you’d like to try Stella 4d for yourself, please visit www.software3d.com/stella.php.
Eighteen Stars
Image
RobertLovesPi.net 