This tessellation appears, at first, to be regular (or “Archimedean,” by analogy with the Archimedean solids), for all of the polygons included are regular. However, it is not vertex-transitive, which keeps it from qualifying as a regular or Archimedean tessellation.
This is the truncated cube, one of the thirteen Archimedean solids.
If the truncation-planes are shifted, and increased in number, in just the right way, this variation is produced. Its purple faces are regular dodecagons, and the orange faces are kites — two dozen, in eight sets of three.
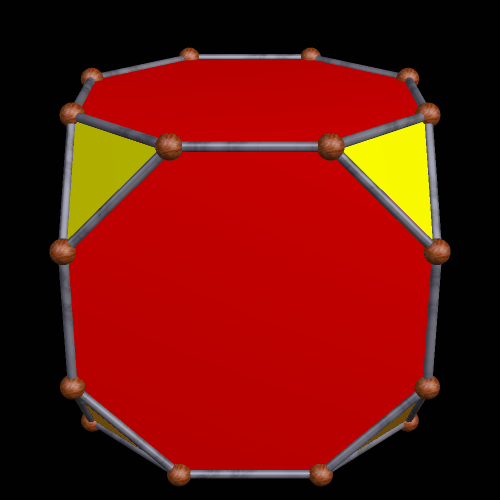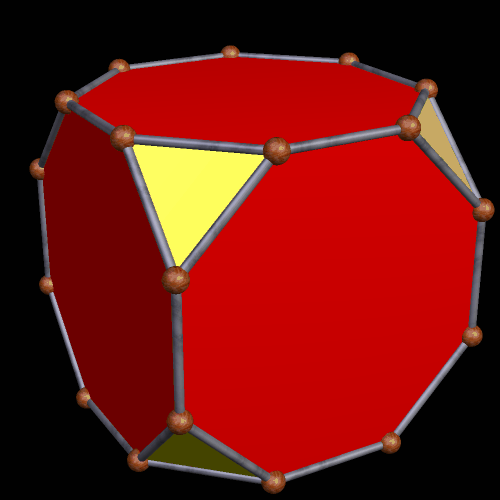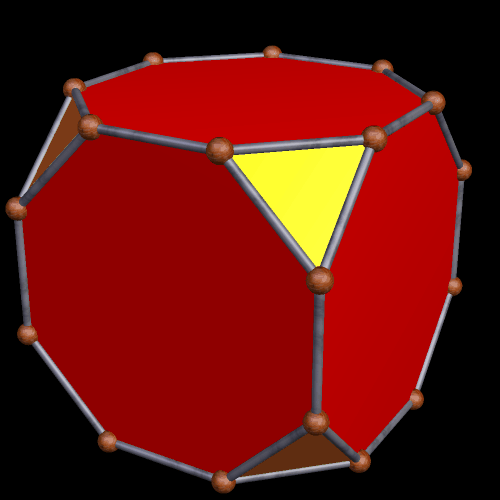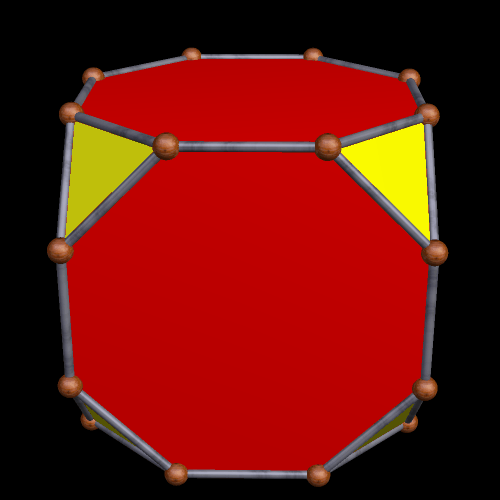
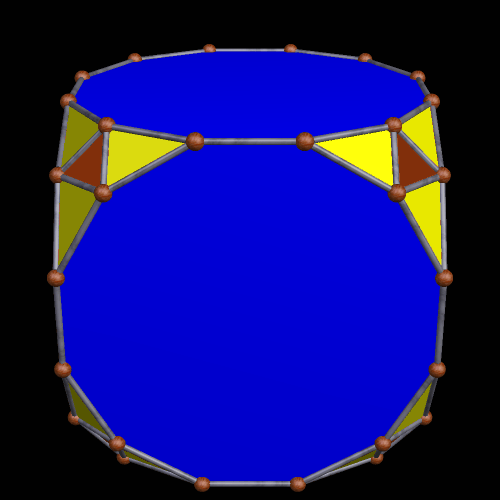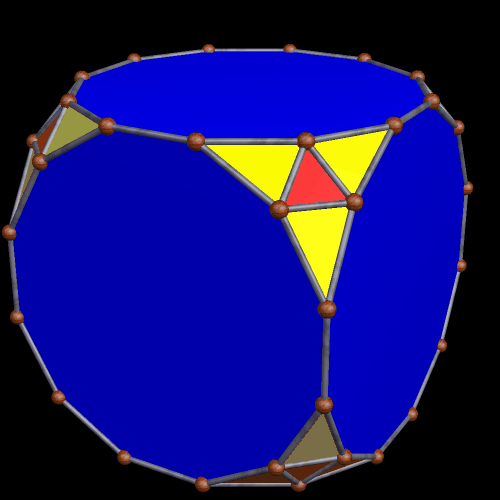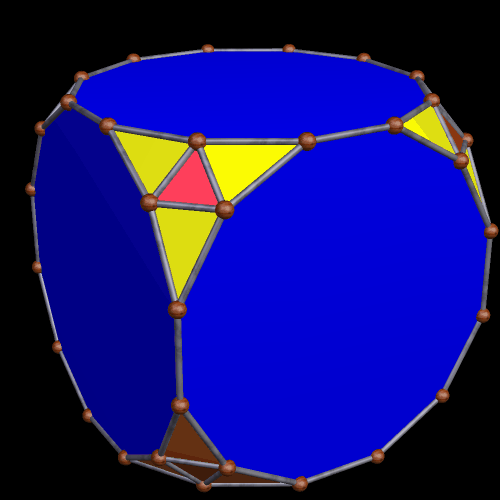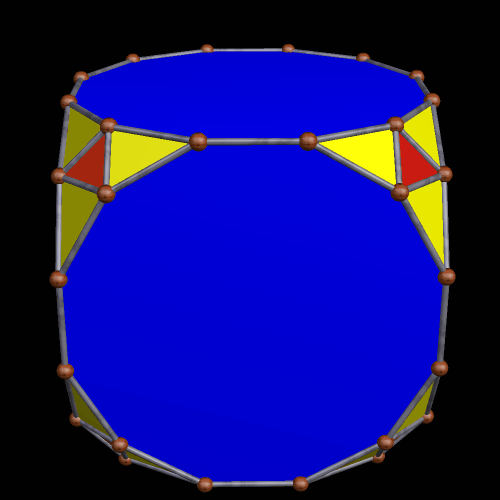
Applying yet another truncation, of a specific type, produces the next polyhedron. Here, the regular dodecagons are blue, and the red triangles are equilateral. The yellow triangles are isosceles, with a vertex angle of ~41.4 degrees.
All three of these images were produced using Stella 4d, available at this website.
RobertLovesPi.net 