The only difference between these two images is that the lower one is in “rainbow color mode.” Both were created using Stella 4d, which you can try for free at this website.
I once made a physical model of this thing, when I was still new to the study of polyhedra. I wish I still had it, but it was lost many years ago.
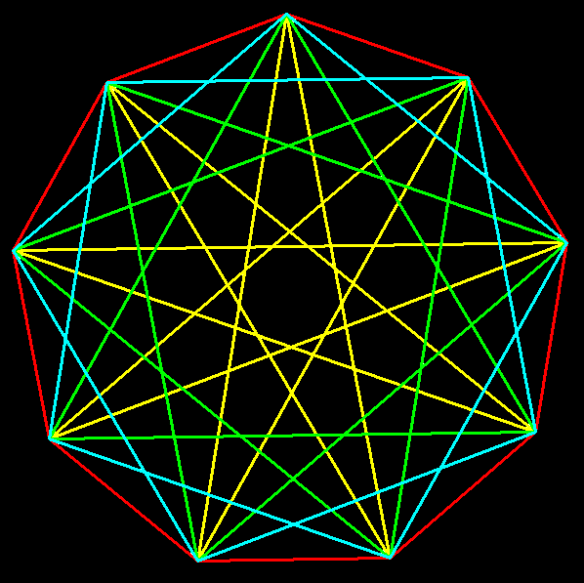
The red figure above is a regular enneagon, or nine-sided polygon, and it has three regular enneagrams (or “star enneagons”) inside it. The light blue figure is called a {9,2} enneagram. The green figure can be viewed two ways: as a {9,3} enneagram, or as a compound of three equilateral triangles. Finally, the yellow figure is a {9,4} enneagram.
To see what these numbers in braces mean, just take a look at one of the yellow enneagram’s vertices, then follow one of the yellow segments to the next vertex it touches. Count the vertices which are skipped, and you’ll notice each yellow segment connects every fourth vertex, giving us the “4” in {9,4}. The “9” in {9,4} comes from the total number of vertices in this enneagram, as well as the total number of segments it has. The blue and green enneagrams are analogous to the yellow one. These pairs of numbers in braces are known as Schläfli symbols.
I should mention that some people call these figures “nonagons” and “nonagrams.” Both “ennea- and “nona-” refer to the number nine, but the latter prefix is derived from Latin, while the former is based on Greek. I prefer to use the Greek, since that is consistent with such Greek-derived words as “pentagon” and “hexagon.”
Finally, there is also an “enneagram of personality,” in popular culture, which some use for analyzing people. Aside from this mention of it, that figure is not addressed here — nor is the nine-pointed star used as a symbol for the Bahá’í faith. However, it’s easy to find information on those things with Google-searches, for those who are interested.
You can’t see the octahedron; it’s hidden at the center of the figure.
I used Stella 4d to make this. You can try that program for yourself at http://www.software3d.com.
I used software called Stella 4d: Polyhedron Navigator to make this shape, and you can try Stella for free, right here. Sometimes, I use a lot of polyhedral modifications with this program, simply looking for a solid which looks interesting. With some polyhedra found through this random-walk process, I can’t even remember exactly how I created them in the first place — and this is one of those times.
I do know that this polyhedron has cuboctahedral symmetry, also known as octahedral symmetry. If anyone can figure out more about it, especially how to construct it, you are invited to share your insights in a comment.
I stumbled upon this zonohedron by adding zones to a truncated octahedron, based on its faces, edges, and vertices. It was created using Stella 4d, which you may try for free at http://www.software3d.com/Stella.php. To the best of my recollection, this is the only zonohedron I have seen which includes rhombi, hexagons, octagons, and, of course, the red hexadecagons.
I’ve been asked this question at least a hundred times. The answer is that my favorite color is black.
Black has been my favorite color for decades. As a college freshman, I even kept a black posterboard up on the wall, in my room at the dorm. Also, I don’t think I have ever been afraid of the dark. I actually find darkness comforting.
I usually get a protest, as a response, when I give my simple answer to this question: “Black’s not a color!”
At that point, nearly every time, I can end debate with a single question to my inquisitor: “What color is your t-shirt?” Sometimes they even look down at their shirt when I say this, and here’s what they typically see:
I have no explanation for why the people who ask me to identify my favorite color are usually wearing black, but at least it quickly ends the conversation.
RobertLovesPi.net 