I made this years ago — in 2010 — and just found it today, on Facebook. That was two years before this blog started. I like finding such “lost works,” but it doesn’t happen often these days.
An Enneagonal Mandala
Reply
Tag Archives: enneagon
Four Polyhedra Featuring Enneagons
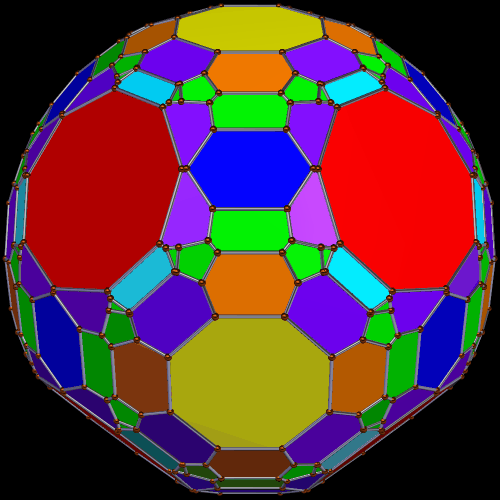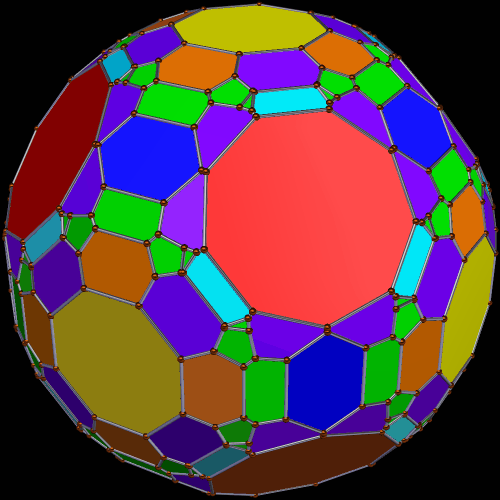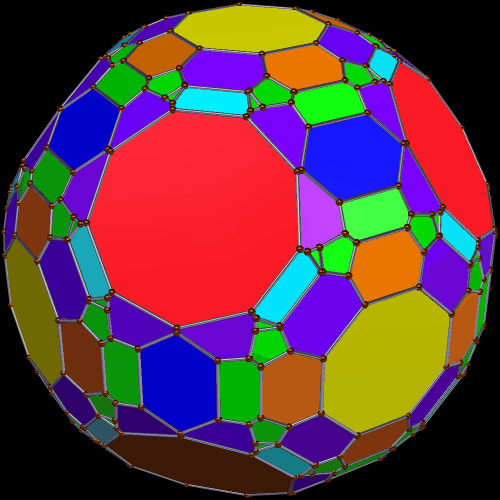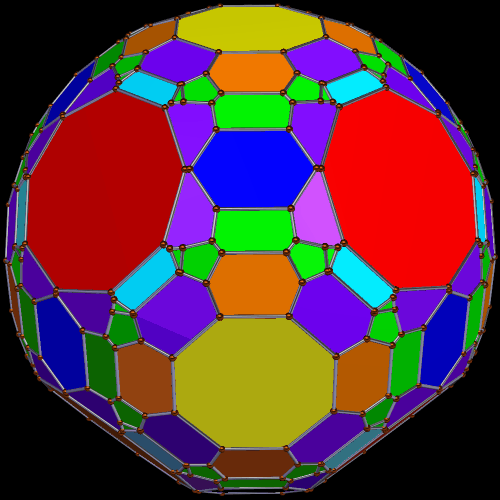
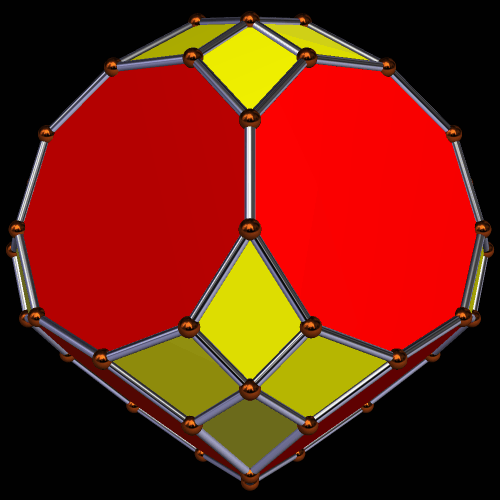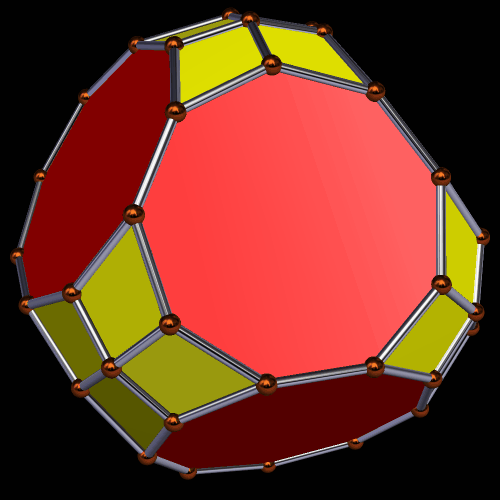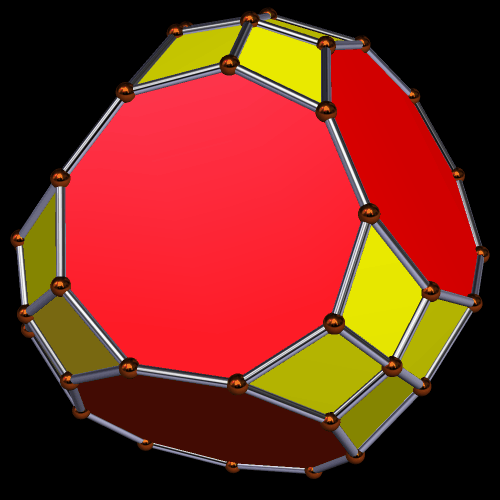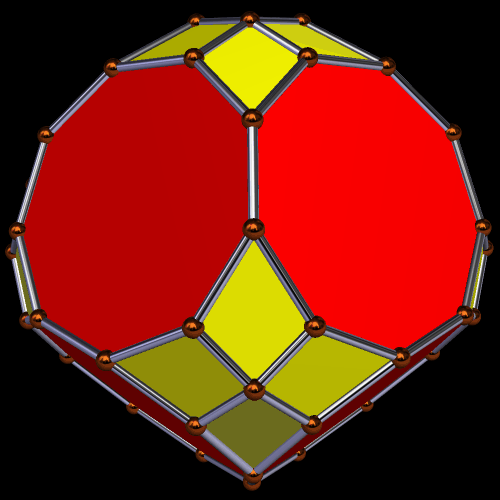
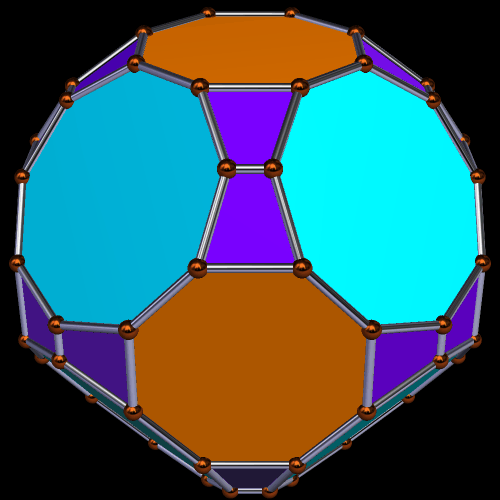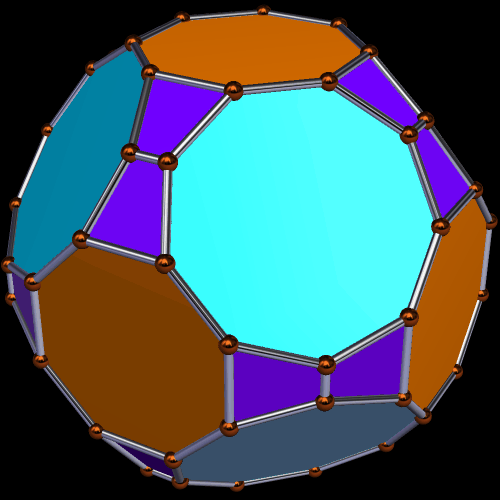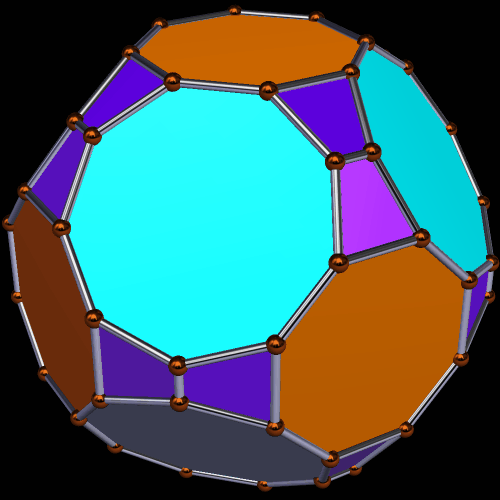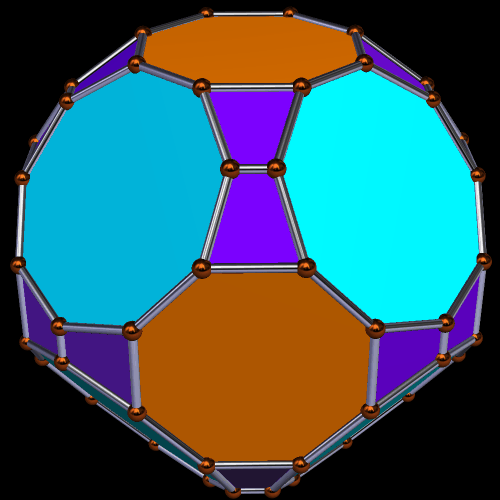
Enneagons are also called nonagons; they are polygons with nine sides. I used Stella 4d to make these four rotating polyhedra, and you may try this program for yourself at http://www.software3d.com/Stella.php.
Tessellation of Blue Triangles and Yellow Concave Pentagons
Alternately, this can be seen as a tessellation of blue diconcave hexagons and yellow triconcave enneagons. Which do you see?
Two Polyhedra, Each Featuring Enneagons and Octagons
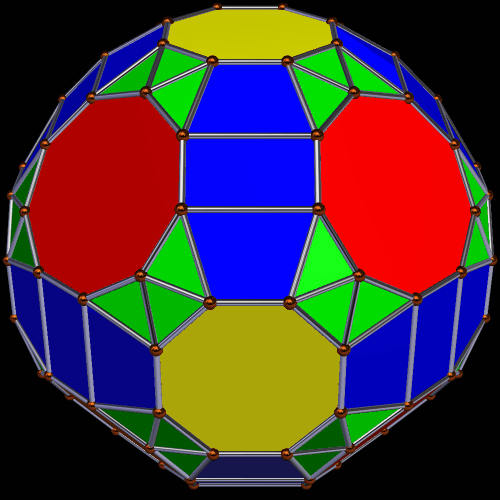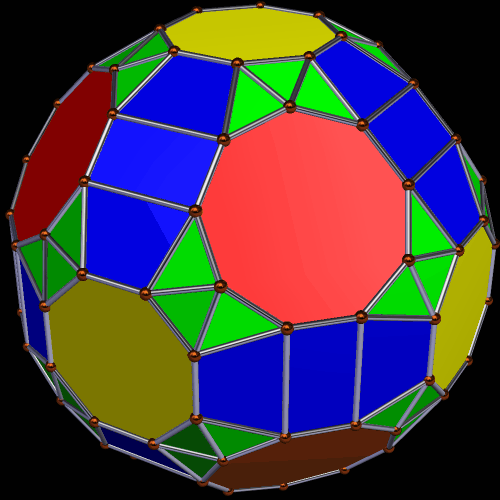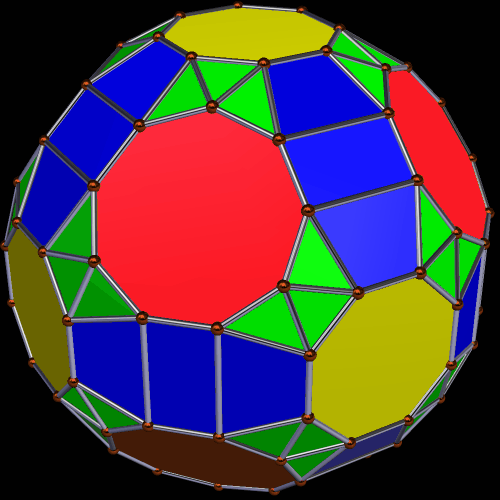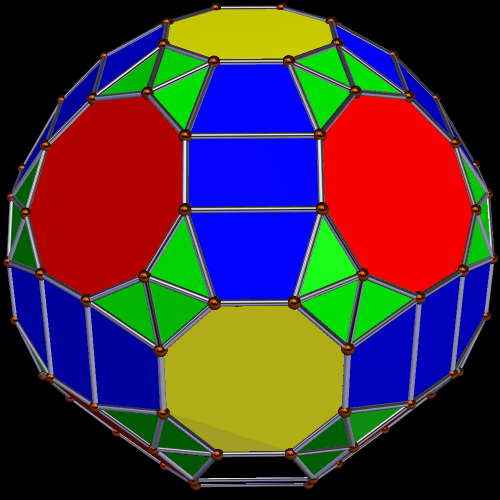
I used Stella 4d: Polyhedron Navigator to make these. You can try it for yourself at http://www.software3d.com/Stella.php.
A Polyhedron Made of Enneagons and Pentagons
This polyhedron has 20 enneagons and 12+60=72 pentagons (of two types) as faces. I made it using Stella 4d, which is available at http://www.software3d.com/Stella.php.
Tessellation Featuring Regular Enneagons, Regular Hexagons, and Isosceles Triangles
Image
Tessellation Featuring Regular Enneagons and Hexaconcave, Equilateral Dodecagons
Image
When We Build Our Dyson Sphere, Let’s Not Use Enneagonal Antiprisms
Before an undertaking as great as building a Dyson Sphere, it’s a good idea to plan ahead first. This rotating image shows what my plan for an enneagonal-antiprism-based Dyson Sphere looked like, at the hemisphere stage. At this point, the best I could hope for is was three-fold dihedral symmetry.
I didn’t get what I was hoping for, but only ended up with plain old three-fold polar symmetry, once my Dyson Sphere plan got at far as it could go without the unit enneagonal antiprisms running into each other. Polyhedra-obsessives tend to also be symmetry-obsessives, and this just isn’t good enough for me.
If we filled in the gaps by creating the convex hull of the above complex of enneagonal antiprisms, in order to capture all the sun’s energy (and make our Dyson Sphere harder to see from outside it), here’s what this would look like, in false color (the real thing would be black) — and the convex hull of this Dyson Sphere design, in my opinion, especially when colored by number of sides per face, really reveals how bad an idea it would be to build our Dyson sphere in this way.
We could find ourselves laughed out of the Galactic Alliance if we built such a low-order-of-symmetry Dyson Sphere — so, please, don’t do it. On the other hand, please also stay away from geodesic spheres or their duals, the polyhedra which resemble fullerenes, for we certainly don’t want our Dyson Sphere looking like all the rest of them. We need to find something better, before construction begins. Perhaps a snub dodecahedron? But, if we use a chiral polyhedron, how do we decide which enantiomer to use?
[All three images of my not-good-enough Dyson Sphere plan were created using Stella 4d, which you can get for yourself at this website.]
Three Convex Polyhedra with Tetrahedral Symmetry, Each Featuring Four Regular Enneagons
In addition to the four regular enneagons, the polyhedron above also has rhombi and isosceles triangles as faces. The next one, however, adds equilateral triangles, instead, to the four regular enneagons, along with trapezoids and rectangles.
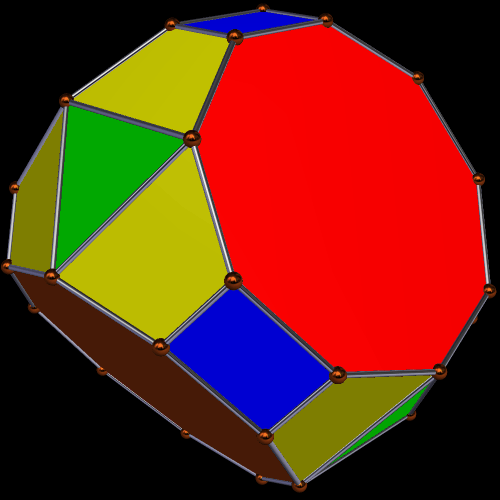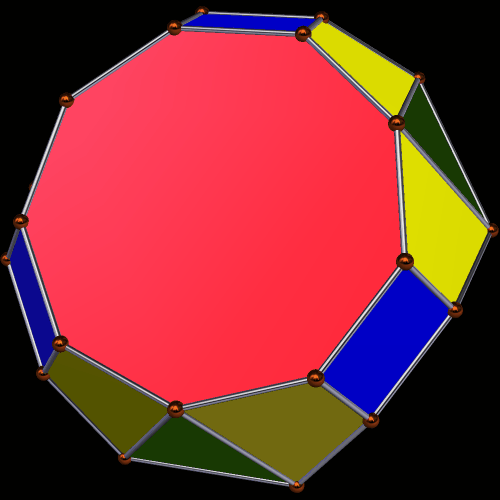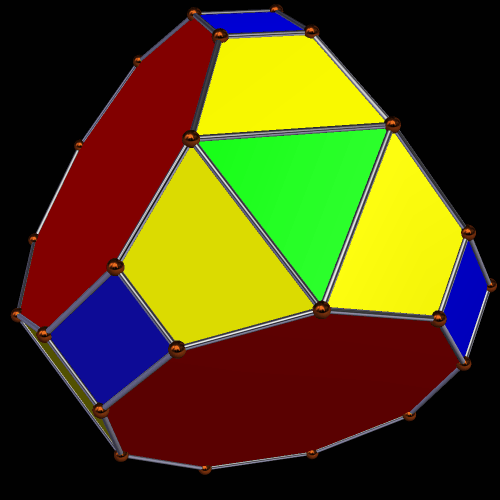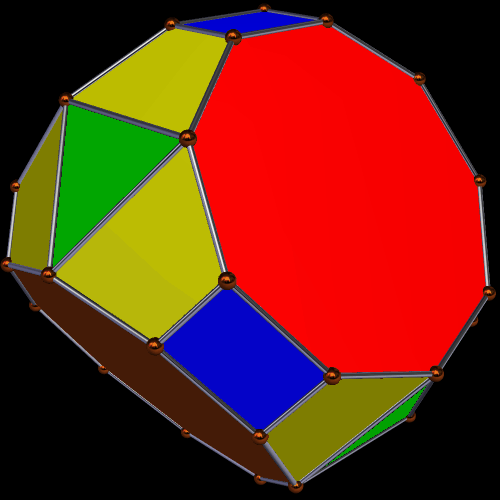
Only the last of these three truly deserves to be called a symmetrohedron, in my opinion, for both its hexagons and enneagons are regular. Only the “bowtie trapezoid” pairs are irregular.
All three of these polyhedra were created using software called Stella 4d: Polyhedron Navigator, which I use frequently for the blog-posts here. You can try it for free at this website.
A Mandala Made of Hexagons, Enneagons, and Dodecagons
I recently re-discovered this “lost work,” which I made using Geometer’s Sketchpad, in 2011 — before I started this blog, which is why it has not appeared here before.
RobertLovesPi.net 