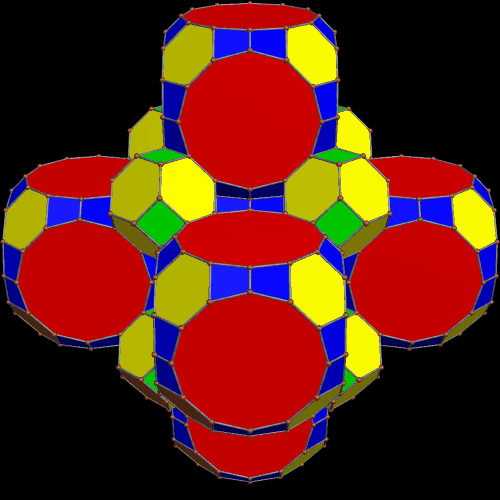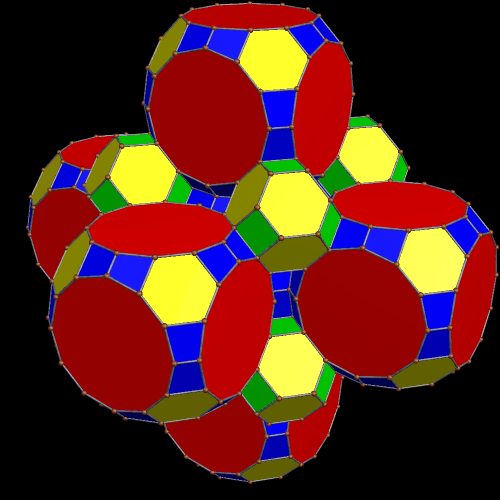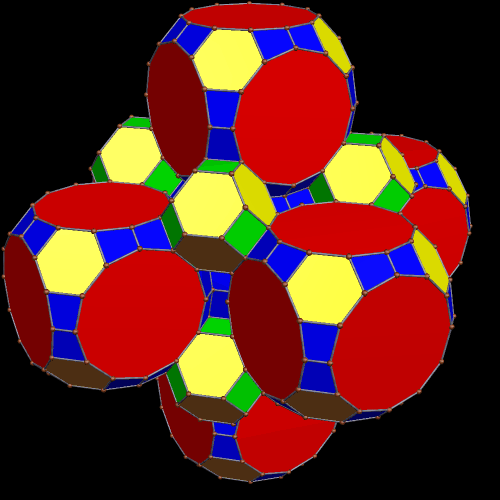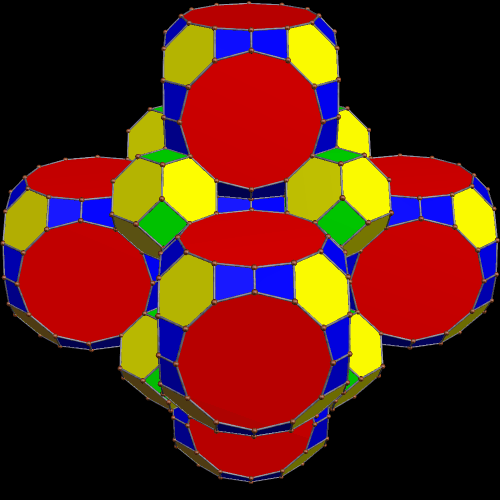
The design on each face of these great rhombcuboctahedra is made from 19 circles, and was created using both Geometer’s Sketchpad and MS-Paint. I then used a third program, Stella 4d (available here), to project this image on each of a great rhombcuboctahedron’s 26 faces, creating the image above.
If you watch carefully, you should notice an odd “jumping” effect on the red, octagonal faces in the polyhedron above, almost as if this polyhedron is suffering from an anxiety disorder, but trying to conceal it. Since I like that effect, I’m leaving it in the picture above, and then creating a new image, below, with no “jumpiness.” Bragging rights go to the first person who, in a comment to this post, figures out how I eliminated this anxiety-mimicking effect, and what caused it in the first place.

Your first hint is that no anti-anxiety medications were used. After all, these polyhedra do not have prescriptions for anything. How does one “calm down” an “anxious” great rhombcuboctahedron, then?
On a related note, it is amazing, to me, that simply writing about anxiety serves the purpose of reducing my own anxiety-levels. It is an effect I’ve noticed before, so I call it “therapeutic writing.” That helped me, as it has helped me before. (It is, of course, no substitute for getting therapy from a licensed therapist, and following that therapist.) However, therapeutic writing can’t explain how this “anxious polyhedron” was helped, for polyhedra can’t write.
For a second hint, see below.
.
.
[Scroll down….]
.
.
Second hint: the second image uses approximately twice as much memory-storage space as the first image used.