Each circle shown is in one of the reflection-planes of this polyhedron, which is the dual of the icosidodecahedron, an Archimedean solid.
(Software credit: see http://www.software3d.com/stella.php)
The icosidodecahedron and the rhombic triacontahedron, duals to each other, are the shapes with red edges showing. I made this using Stella 4d, which you may try for free at http://www.software3d.com/stella.php.
There are many ways to make intermediate forms between dual polyhedra. This was made using the expansion method. The faces of the icosidodecahedron (red and blue) were moved outward, as were the green faces of the rhombic triacontahedron, until the meeting of all possible vertices. The yellow rectangles were the spaces created between faces by this expansion.
(Software credit: see http://www.software3d.com/stella.php)
One of many photographs of Saturn provided by the Cassini spacecraft, and then projected onto the faces of a rhombic triacontahedron with the software available at http://www.software3d.com/stella.php.
Rhombic triacontahedra make quite versatile building-blocks for creating clusters in the shapes of other polyhedra. In this image (created with software you can find at http://www.software3d.com/Stella.php), a collection of them forms the overall shape of an octahedron.
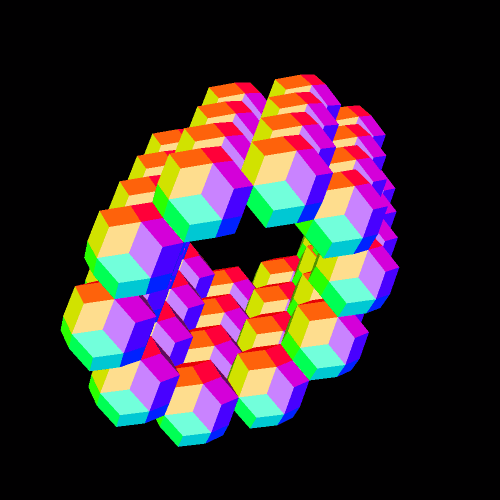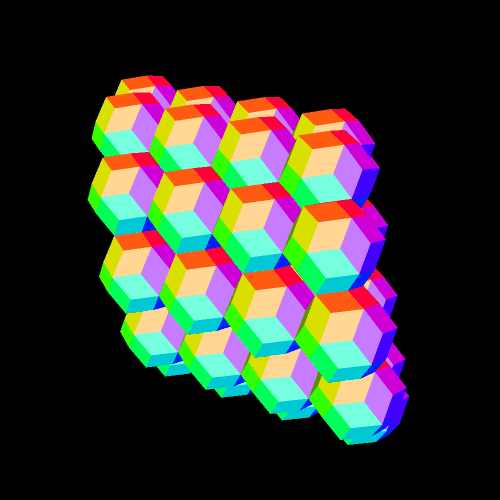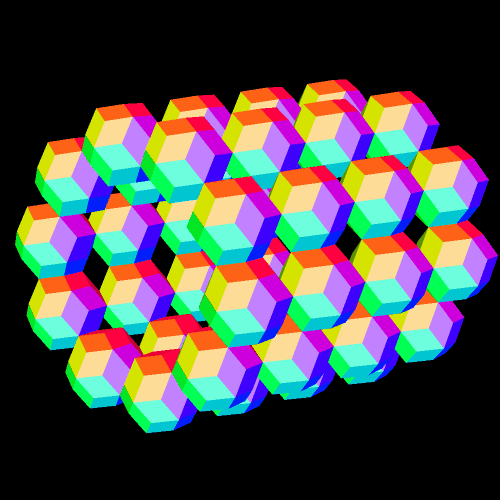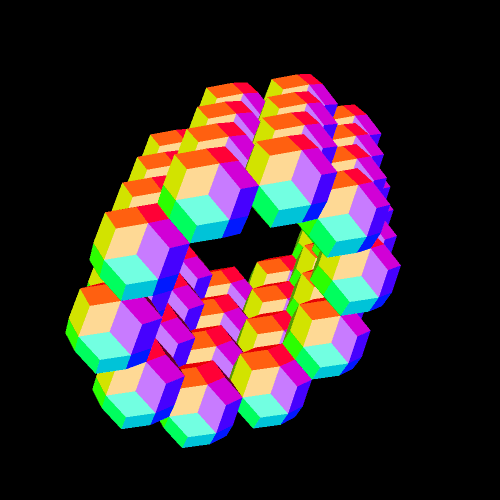
The software used to make this is available as a free trial download at http://www.software3d.com/stella.php.
I made this .gif with Stella 4d, software available as a free trial download at http://www.software3d.com/stella.php.
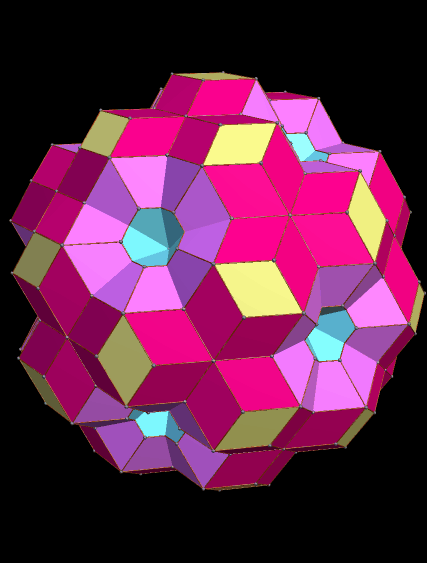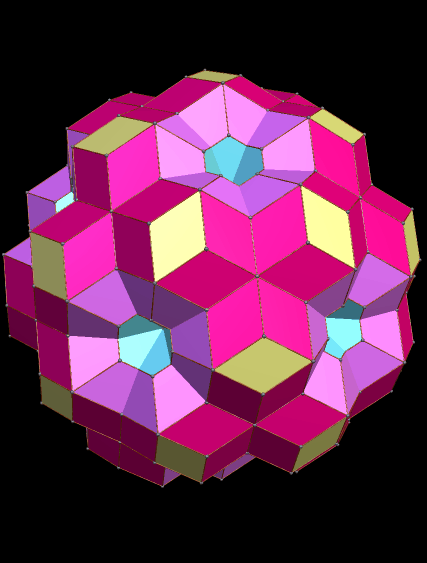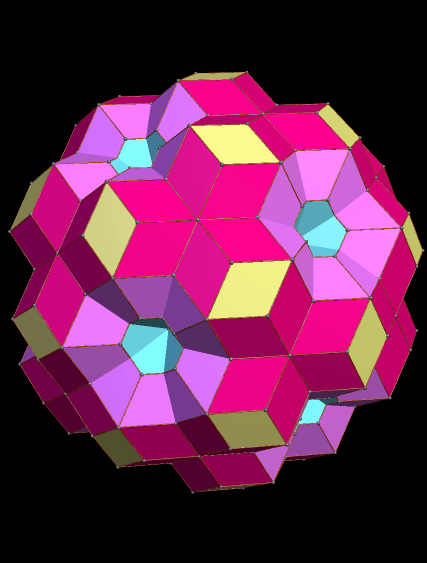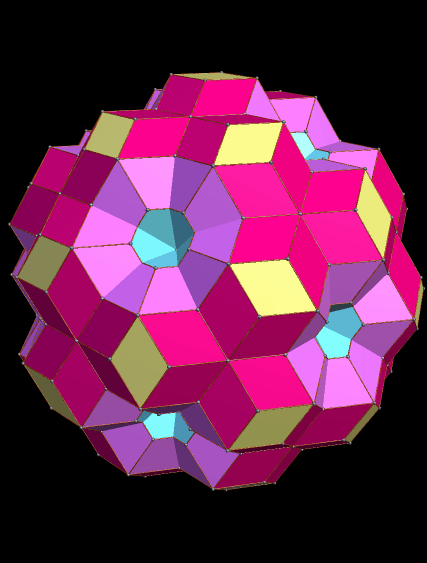
In the last post, I showed you a cluster of rhombic triacontahedra (RTCs) which took a long time to build, for I had to carefully choose which faces to augment (attach) with new RTCs.
This one, by contrast, was very fast. I simply took one RTC, and augmented all thirty faces with RTCs. Unlike the RTCs in the last post, these intersect — the primary reason its appearance is so different.
In this polyhedron, many familiar polyhedra are defined. The yellow rhombi, for example, are found at the vertices of an icosidodecahedron. The blue “holes” have their centers at the vertices of an icosahedron, and the pink areas’ centers are at the vertices of a dodecahedron.
If you follow this blog closely, you have noticed that I always include this link (http://www.software3d.com/Stella.php) any time I post images made with the program I use for creating these. It’s called Stella 4d: Polyhedron Navigator. With it, you can create things of beauty, combining simplicity and complexity, which no one has ever seen before. A friend of mine on the other side of the planet wrote it, and I always include this link, where people can try or buy this software, as a way to thank him for doing so. For investigations of polyhedra, I know of no better tool.
Rhombic triacontahedra, due to their multiple symmetries, make excellent building blocks to make shapes resembling other polyhedra. This icosahedral cluster is far from being the only such possible “cluster” polyhedron made entirely of rhombic triacontahedra.
This .gif was created with Stella 4d, software you may find here: http://www.software3d.com/Stella.php.
RobertLovesPi.net 