May | 2014 | RobertLovesPi.net

Tessellation Featuring Regular Dodecagons, Regular Octagons, Squares, and Hexaconcave, Equilateral Dodecagons

Image

Tessellation Featuring Regular Dodecagons, Regular Octagons, Squares, and Hexaconcave. Equilateral Dodecagons

Three-Color Arrangement for the Dodecahedron

Image

Three-Color Arrangement for the Dodecahedron

There are well-known symmetrical 4- and 6-color arrangements for the dodecahedron, and the rhombic dodecahedron has such arrangements in 3, 4, and 6 colors. What’s different about the (Platonic) dodecahedron that the 3-color arrangement you see here doesn’t make the cut, yet there is one for the rhombic dodecahedron?

The answer: in the other arrangements mentioned, faces of the same color do not share edges. Here, they do, so this one is usually not listed with the others.

Software credit: please visit http://www.software3d.com/Stella.php and try the free download of Stella 4d available there. It’s the program I used to make this image. And, as for the color arrangements mentioned above, they’re pre-loaded into the Stella interface as easy-to-find options.

James Randi, on the Limited Effectiveness of Belief

Image

James Randi, On the Effectiveness of Belief

One of the high points of my life was the day I got to have several conversations with James Randi. I enjoyed them. Some others who were there, though, not so much.

An example of how one of the question-and-answer sessions went:

Question: What happens to us after we die?
Randi’s answer: What happens to a computer after you turn off the power?

Apparently the questioner was rather upset by this reply, but I didn’t figure that out myself, even though I was present. I learned about it later, from others. Randi’s response simply made sense to me.

The Vacuum Cleaner Enigma

Image

The Vacuum Cleaner Enigma

A vacuum is, by definition, a region of space devoid of matter. While a perfect vacuum is a physical impossibility, very good approximations exist. Interplanetary space is good, especially far from the sun. Interstellar space is better, and intergalactic space is even better than that.

Along come humans, then, and they invent these things:

. . . and call them “vacuum cleaners.”

Now, this makes absolutely no sense. There isn’t anything cleaner than a vacuum — and the closer to an ideal vacuum a real vacuum comes, the cleaner it gets. Since vacuums are the cleanest regions of space around already, why would anyone pay good money for a machine that supposedly cleans them? They’re already clean!

Even cleaning in general is a puzzle, without vacuums being involved at all. To attempt to clean something — anything — is, by definition, an attempt to fight the Second Law of Thermodynamics. Isn’t it obvious that any such effort is, in the long run, doomed from the outset?

—–

[Image note: I didn’t create the images for this post, but found them using Google. I assume they are in the public domain.]

A Triangle, The Equilateral Triangles on Its Sides, and the Vertex-Centered Circles for Which Its Sides Are Radii

Image

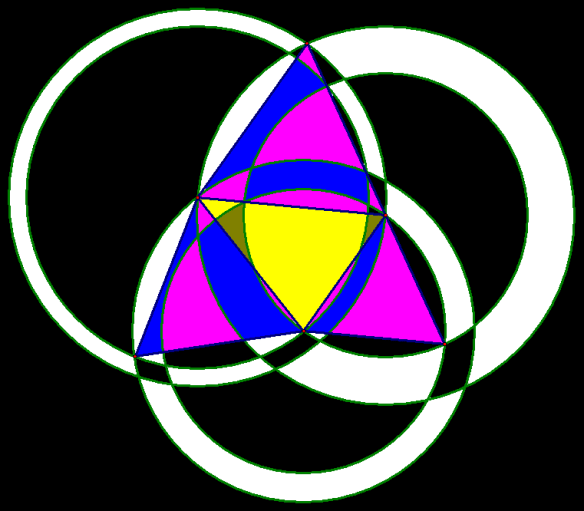
A Triangle, The Equilateral Triangles on Its Sides, and The Circl

Statement of the Obvious, in Venn Diagram Form

Image

Statement of the Obvious, in Venn Diagram Form

Fifteen

Image

Fifteen

On the Constructible Angles

Image

The Constructible Angles

The Ancient Greeks figured out how to combine the Euclidean constructions of the regular pentagon and triangle to obtain constructions for the regular pentadecagon, which has central angles (between adjacent radii) of 360/15 = 24 degrees. Here’s an example, showing how this can be performed:

Also, it’s easy to construct an equilateral triangle, and then bisect an angle of it, to obtain a 30 degree angle.

The existence of angle difference identities in trigonometry is tied to the fact that you can subtract angles, on paper, with Euclidean constructions. Therefore, an angle of 24 degrees may be subtracted from a 30 degree angle to obtain a 6 degree angle. This can be bisected to get a 3 degree angle, and then bisected again to obtain a 1.5 degree angle, then a 0.75 degree angle, and so on.

However, a one degree angle is impossible to construct. Were this not the case, a 24 degree angle’s constructibility would imply that of the 23 degree angle, by subtraction of a one degree angle. After that, subtract three degrees more, and you have a 20 degree angle . . . and with that, you can construct a regular enneagon, also known an a nonagon. But we know — it has been proven — that regular enneagons have no valid Euclidean constructions. Therefore, one degree angles are also non-constructible, by reductio ad absurdam.

Carl Friedrich Gauss’s much more recent proof (1796; he was 19 years old) that a regular polygon of 17 sides can also be constructed — the first significant advance in this field since the time of the ancient Greeks — adds more constructible angles. Building on his work, other mathematicians have also shown that regular polygons with 257 and 65,537 sides can also be constructed, adding yet more constructible angles, but they are all for angles measuring fractional numbers of degrees, since none of these numbers are factors of 360, which equals (2³)(3²)(5). It’s also possible to combine these possible constructions to construct more regular polygons, as was shown above for the pentadecagon. For example, one can construct a regular pentagon with 51 sides, since 51 = (17)(3) — but, again, combinations of this type only lead to possible constructions of angles with measures which are fractional numbers of degrees. For angles with degree measures which are integers, it’s multiples of three — and that’s it.

[Note regarding images: the photograph of a compass at the top of this page was not taken by me, but simply found with a Google image-search. The pentadecagon-construction image, though, I did make, using both Geometer’s Sketchpad and MS-Paint.]