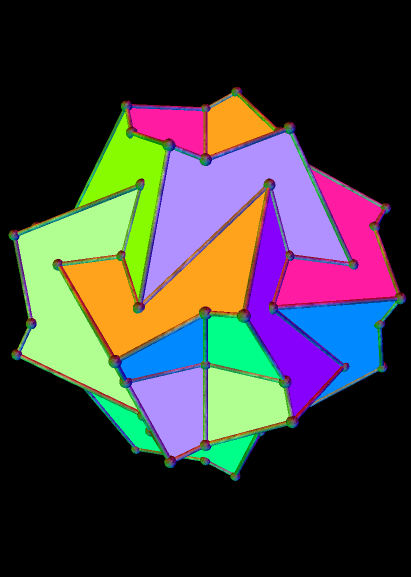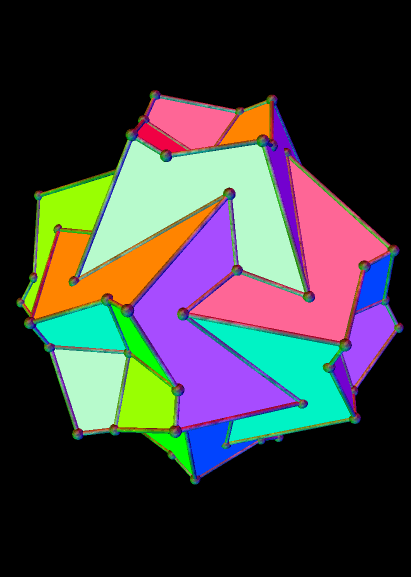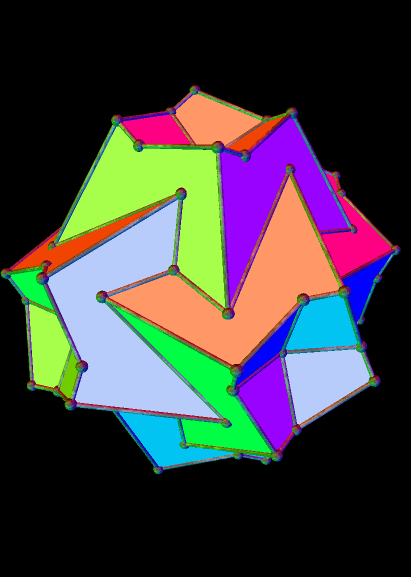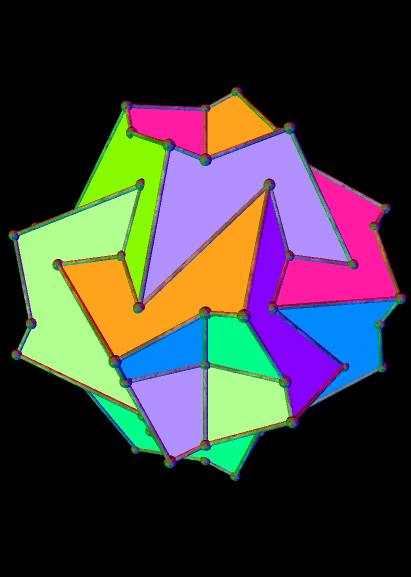
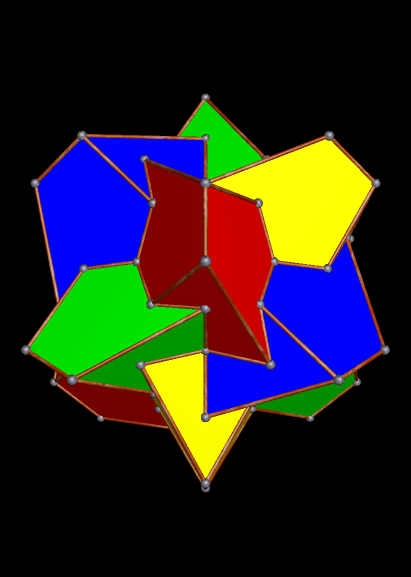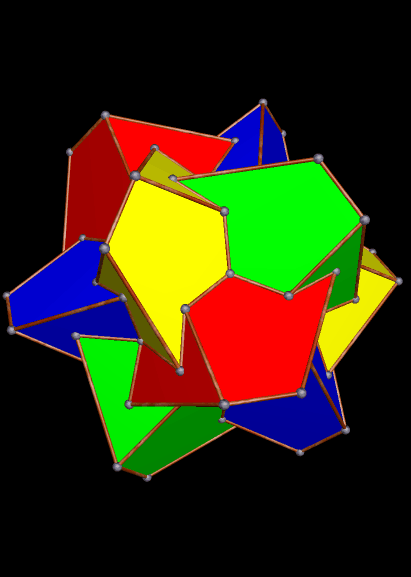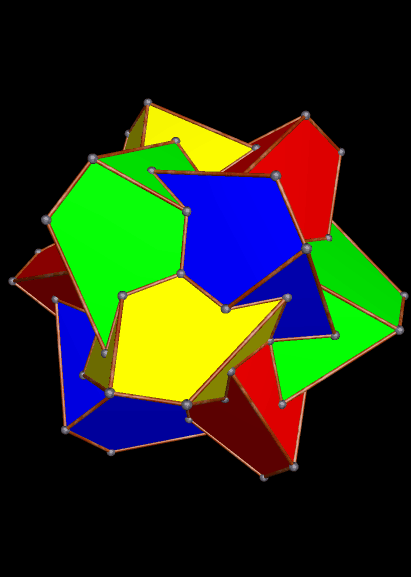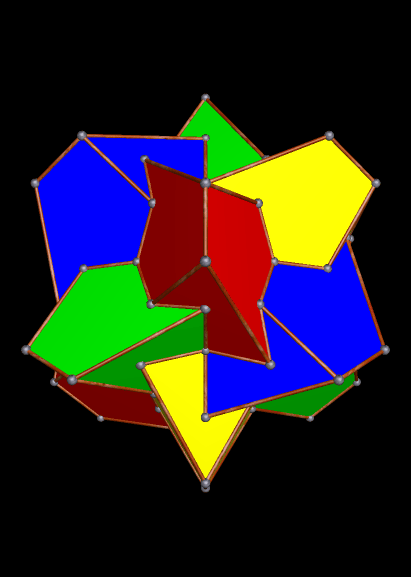
In the image above, which I stumbled upon using Stella 4d (available here), the tetrahedra are elongated. If they are regular, instead, the same arrangement looks very different:
Two Compounds of Six Tetrahedra Each
Reply
Monthly Archives: September 2014
Selections from the Stellation-Series of the Strombic Icositetrahedron, Including Some Polyhedral Compounds
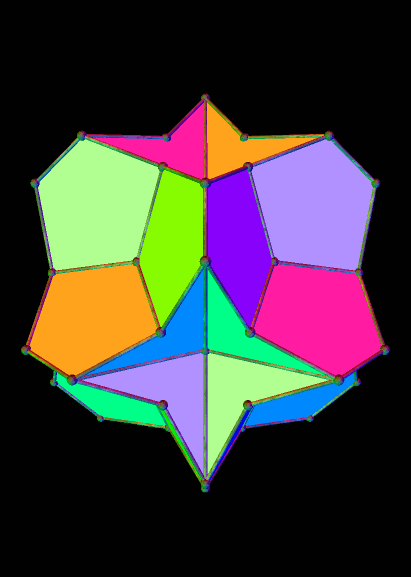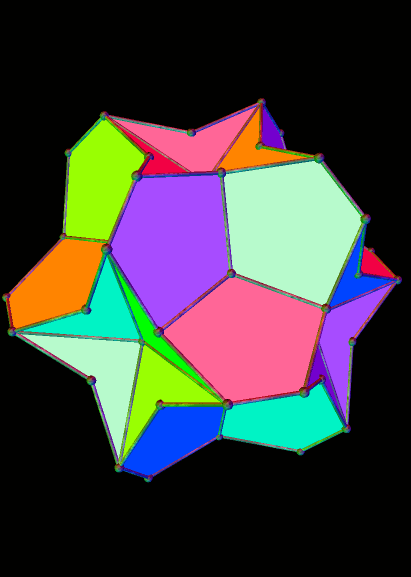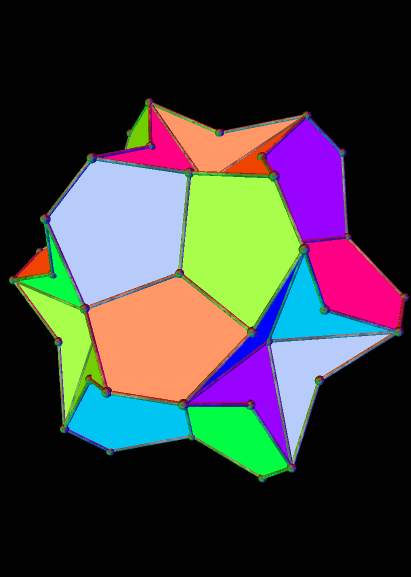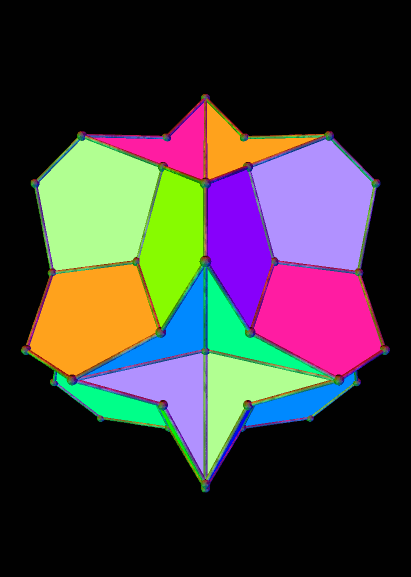
The strombic icositetrahedron is the dual of the rhombcuboctahedron, and has many interesting polyhedra in its stellation-series. Here are a few of them, starting with the 10th stellation.
Here’s the strombic icositetrahedron’s 16th stellation:
And the 19th:
And the 21st:
And the 23rd:
And the 25th:
And the 26th:
Next, the 28th stellation. It isn’t colored as the other stellations above are colored, simply because it is also a compound of six off-center square-based pyramids.
The 34th stellation is even more interesting. It’s a symmetrical four-part compound, but the component polyhedra have irregular faces, and are much less symmetrical than the compound itself.
Here is the 37th stellation in this series:
And the 43rd:
And the 44th:
The 59th stellation in this series is an octahedron, with each face excavated by short, triangle-based pyramids. It can also be seen as a compound of three shortened square-based dipyramids, but coloring it as a compound proved difficult, so it is presented here in rainbow-color mode:
Here’s the 61st stellation:
And the 68th:
And the 71st:
And the (quite different from the 71st) 72nd stellation:
And the 73rd:
And, finally, the 74th, which is an interesting two-part compound.
And the 79th:
And the 82nd stellation:
The last one I’m showing here is the 93rd stellation, another four-part compound.
All these images were created using Stella 4d: Polyhedron Navigator, which you may try for yourself at http://www.software3d.com/Stella.php.
Falling into a Vortex
Compound of Three Eight-Faced Trapezohedra
I made this using Stella 4d, which you can try right here. In addition to being a compound of trapezohedra, it is also the sixth stellation of the triakis octahedron, the dual of the truncated cube.
Fort Smith? Pine Bluff? What’s the Difference?
Unless you also live in the American state of Arkansas, you may not have even heard of Fort Smith and Pine Bluff. For those who grew up in this state, though, they’re considered (by our peculiar standards) to be major cities. Fort Smith is on the far West side of the state, on the Oklahoma border, while Pine Bluff is in the Southeastern part of the state, also known as the Mississippi Delta.
I didn’t learn Arkansas geography in school. Instead, when I was a child, my family traveled, mostly within the state — a lot. By the time I was ten years old, I’d been in all 75 counties of Arkansas, and knew quite a bit about where things are here . . . except for these two cities, Fort Smith and Pine Bluff.
If you’re from Arkansas, you know these two cities are nothing alike. What I noticed in childhood, above all else, was the fact that the two cities smelled so different from each other. The reason is simple: Pine Bluff has a lot of paper mills, and the smell near paper mills is not entirely unlike being locked in a small closet with several dozen rotten eggs. Fort Smith, by contrast, is relatively odorless.
What perplexed my parents, though, is the fact that I would consistently confuse these two cities. I’d refer to the “horrible smell of Fort Smith,” or, if I knew we were going to Pine Bluff, I might ask if we’d be crossing the border into Oklahoma. My parents always corrected these mistakes, but I kept making them, repeatedly, which is not like me at all. When young, I never had more than a 50% chance of correctly identifying either of these cities. Once I figured out what I was doing, though — at around age twelve — this repeated error made perfect sense.
When I try to understand something, I examine it, and consider it, mathematically. Often, I’m not even conscious I’m doing that — it’s simply how I think. Both Fort Smith and Pine Bluff are two-word city names. To make matters even worse, the first word of each city-name has four letters, and the second word in each has five. Once I realized these parallels, though, it all made sense: no wonder I couldn’t tell these places apart, with names which, examined through the lens of childhood mathematics, looked exactly alike.
To my knowledge, no one else has ever had a long-term problem confusing these two Arkansas cities. However, when those who know me well hear this story, they are never surprised that I would do such a thing.
Sam Harris, on Paying Attention
Source: Waking Up: A Guide to Spirituality Without Religion, p. 3.
Four-Part Compound of Thin Parallelopipeds
I made this using Stella 4d: Polyhedron Navigator. You may try this program for free at http://www.software3d.com/Stella.php.
Quadrilaterals with Perpendicular Diagonals
I just learned these things are officially called orthodiagonal quadrilaterals. I’ve been calling them Qw⊥Ds (pronounced “quids”) for years, have studied their properties, and have even tested students’ knowledge of Qw⊥D esoterica.
Obviously, on grounds of symmetry alone, it is easy to determine that Qw⊥Ds include all squares. With congruent triangles, it is also possible to prove that all rhombi, kites, and darts are Qw⊥Ds.
As for other parallelograms, such as the rectangle, they are Qw⊥Ds iff they are also rhombi. No non-rhomboidal parallelograms have perpendicular diagonals.
With no parallel sides, altering darts and kites to make their diagonals off, slightly, from being perpendicular would be easy. In the process, though, the figure would lose its “dartness” or “kiteness.”
With exactly one pair of parallel sides — what most Americans call “trapezoids” (that word has multiple, troublesome definitions) — things get more messy. A non-isosceles trapezoid (lower left) can either have perpendicular diagonals (red) or not (yellow). As can be seen at the lower right, the same is true of isosceles trapezoids.
More Polyhedra, Including Some Compounds, from the Stellation-Series of the Tetrakis Cube
The next one is a compound of eight off-center pyramids. By this point, I had gone so far into the stellation-series (a search I began when preparing the post before this one) that I had lost count.
This one is a compound of three short square-based dipyramids:
This one, according to Stella 4d, is a compound of three parts, but I can’t quite figure out what the parts are!
Here is another “mystery compound,” this one with two parts:
Stella 4d, which I used to make these, may be tried here.
Two Compounds of Dipyramids from the Stellation-Series of the Tetrakis Cube
The 16th stellation of the tetrakis cube, the dual of the truncated octahedron, is a compound of three elongated octahedra, or square dipyramids:
The 65th stellation of this same polyhedron is of another compound of dipyramids, but these are triangular dipyramids with obtuse faces, and there are four of them:
I generated both of these images with Stella 4d: Polyhedron Navigator, available right here.
RobertLovesPi.net 