Two Different Clusters of Thirty-One Rhombicosidodecahedra

Posted on 16 November 2014 by RobertLovesPi

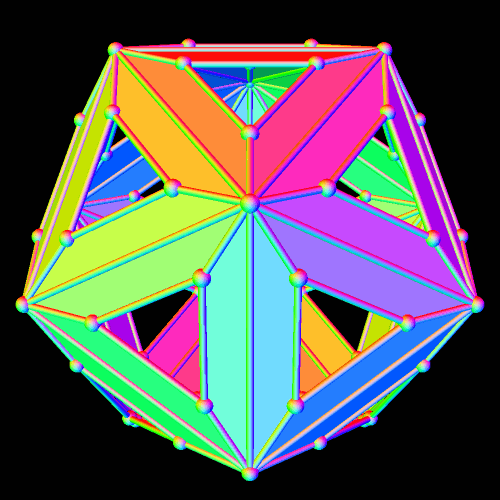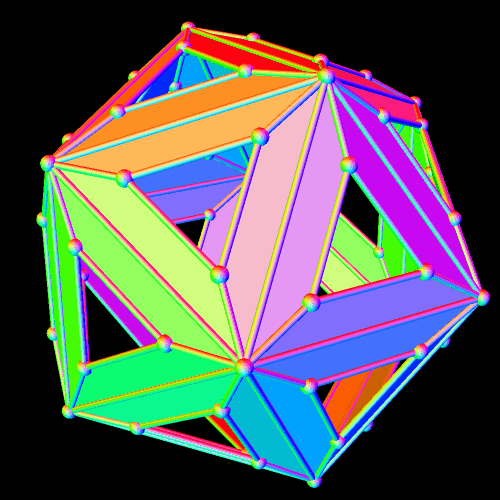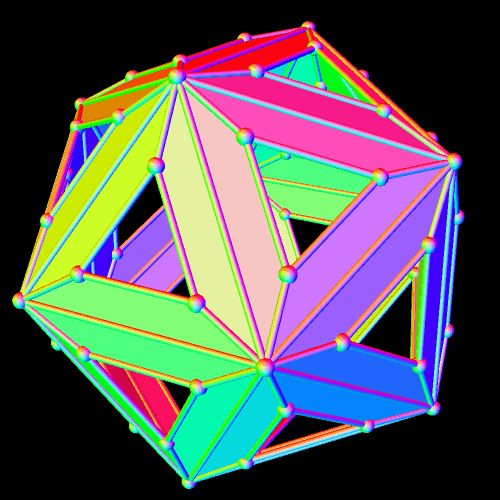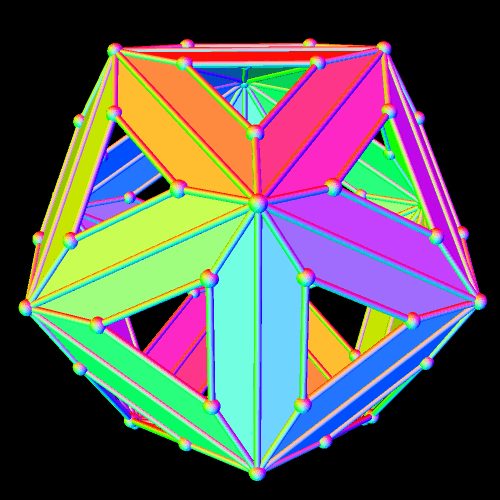
The cluster above was formed by starting with one rhombicosidodecahedron, and then augmenting each of its thirty square faces with another rhombicosidodecahedron. If you examine the single rhombicosidodecahedron below, though, you’ll see that this can be done in two different ways, each of which produces a cluster with the same degree of symmetry as the original. (If less symmetry is acceptable, there are far more than two different ways to obtain such clusters, but that does not interest me.)

When new rhombicosidodecahedra are attached to the square faces of this central rhombicosidodecahedron, they new ones can be oriented such that pentagons are placed above pentagons, and triangles above triangles — or the new ones can be oriented the other way, so that pentagons are placed above triangles, and triangles above pentagons. One of these possibilities produces the cluster at the top of this post. The other possibility produces the cluster shown below.

All of these polyhedral manipulations were performed using a program called Stella 4d: Polyhedron Navigator, which may be purchased (or tried for free, as a trial download) at http://www.software3d.com/Stella.php.

72-Faced Snub Dodecahedron Variant, and Related Polyhedra

Posted on 16 November 2014 by RobertLovesPi

Like the snub dodecahedron itself, which this resembles, this polyhedron is chiral, meaning it exists in left- and right-handed forms. One version is shown above, and its mirror-image is shown below.

With any chiral polyhedron, it is possible to make a compound out of the two mirror-images. Here is the enantiomorphic-pair compound for this polyhedron.

After making this compound, I was curious about what sort of convex hull it would have, so I used the program I employ for these polyhedral investigations, Stella 4d (available at http://www.software3d.com/Stella.php), to find out:

This polyhedron contains irregular icosagons, which are twenty-sided polygons. After playing around with this for a while, I was able to construct a related polyhedron in which the icosagons were regular — and that was one of the polyhedra seen on the post immediately before this one, which I then altered to form the others there. Had I not actually seen it happen myself, I would not have suspected there would be any connection between the snub dodecahedron, and polyhedra containing regular icosagons.

Three Polyhedra, Each Featuring One Dozen Regular Icosagons

Posted on 16 November 2014 by RobertLovesPi

Icosagons are polygons with twenty sides, and do not appear in any well-known polyhedra. The first of these three regular-icosagon-based polyhedra has 122 faces.

The second of these polyhedra, each of which bears an overall resemblance to a dodecahedron, has 132 faces.

Finally, the third of these polyhedra has a total of 152 faces.

I used Stella 4d to make each of these virtual polyhedron models — and you may try this program for free at http://www.software3d.com/Stella.php.

A Polyhedron Featuring Twelve Regular Pentadecagons, and Twenty Regular Enneagons

Posted on 16 November 2014 by RobertLovesPi

In the last post here, there were two polyhedra shown, and the second one included faces with nine sides (enneagons, also known as nonagons), as well as fifteen sides (pentadecagons), but those faces were not regular.

The program I use to manipulate polyhedra, Stella 4d (available at http://www.software3d.com/Stella.php), has a “try to make faces regular” function included. When I applied it to that last polyhedron, in the post before this one, Stella was able to make the twenty enneagons and twelve pentadecagons regular. The quadrilaterals are still irregular, but only because squares simply won’t work to close the gaps of a polyhedron containing twenty regular enneagons and twelve regular pentadecagons. These quadrilaterals are grouped into thirty panels of four each, so there are (4)(30) = 120 of them. Added to the twelve pentadecagons and twenty enneagons, this gives a total of 152 faces for this polyhedron.

A Polyhedral Demonstration of the Fact That Nine Times Thirty Equals 270, Along with Its Interesting Dual

Posted on 16 November 2014 by RobertLovesPi

It would really be a pain to count the faces of this polyhedron, in order to verify that there are 270 of them. Fortunately, it isn’t necessary to do so. The polyhedron above is made of rhombus-shaped panels which correspond to the thirty faces of the rhombic triacontahedron. Each of these panels contains nine faces: one square, surrounded by eight triangles. Since (9)(30) = 270, it is therefore possible to see that this polyehdron has 270 faces, without actually going to the trouble to count them, one at a time.

The software I used to make this polyhedron may be found at http://www.software3d.com/Stella.php, and is called Stella 4d. With Stella 4d, a single mouse-click will let you see the dual of a polyhedron. Here’s the dual of the one above.

This polyhedron is unusual, in that it has faces with nine sides (enneagons, or nonagons), as well as fifteen sides (pentadecagons). However, these enneagons and pentadecagons aren’t regular — yet — but they will be in the next post.

A Polyhedral Demonstration of the Fact That Twenty Times Four Is Eighty

Posted on 16 November 2014 by RobertLovesPi

The Platonic solid known as the icosahedron has twenty triangular faces. This polyhedron resembles the icosahedron, but with each of the icosahedron’s triangles replaced by a panel of four faces: three isosceles trapezoids surrounding a central triangle. Since (20)(4) = 80, it is possible to know that this polyhedron has eighty faces — without actually counting them.

To let you see the interior structure of this figure, I next rendered its triangular faces invisible, to form “windows,” and then, just for fun, put the remaining figure in “rainbow color mode.”

I perform these manipulations of polyhedra using software called Stella 4d. If you’d like to try this program for yourself, the website to visit for a free trial download is http://www.software3d.com/Stella.php.