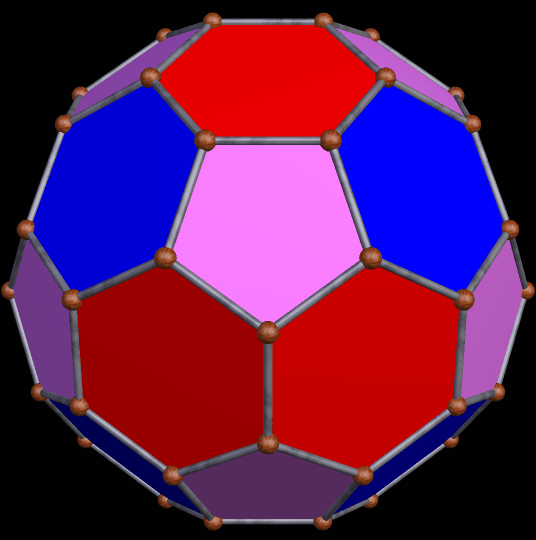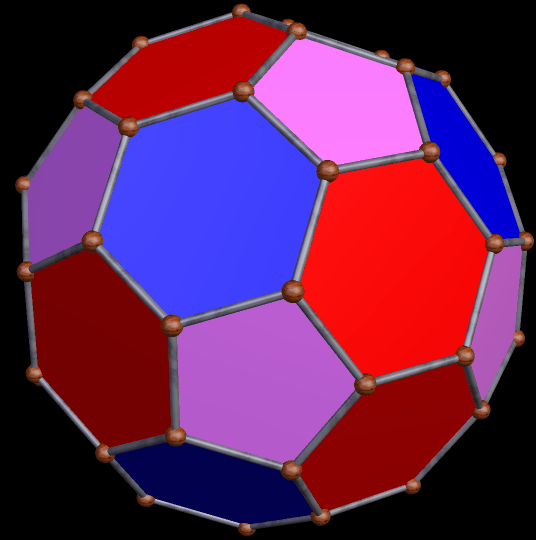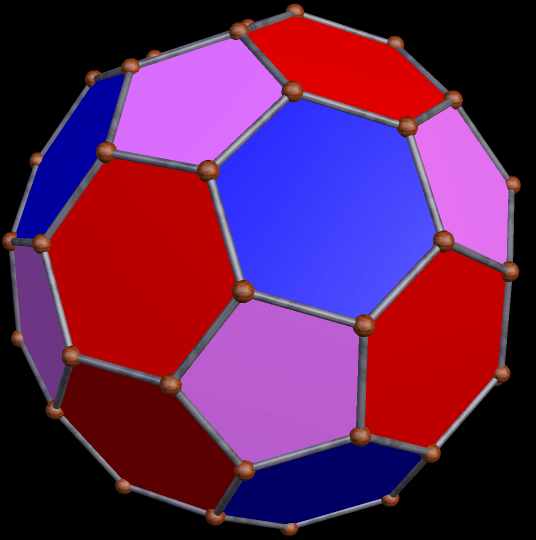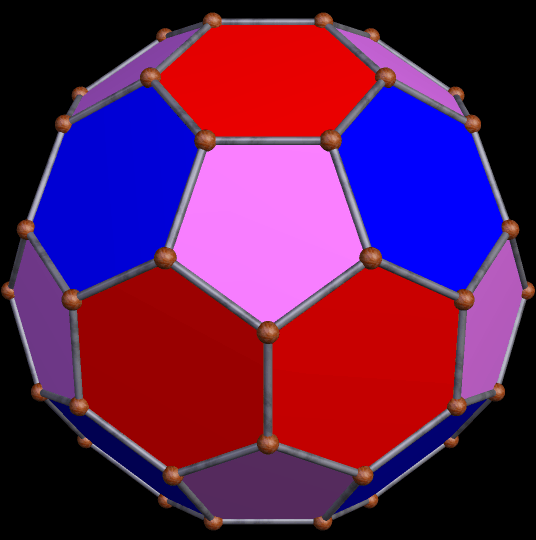
The stellation-series of the rhombic enneacontahedron has many polyhedra which are, to be blunt, not much to look at — but there are some attractive “gems” hidden among this long series of polyhedral stellations. The one above, the 33rd stellation, is the first one attractive one I found — using, of course, my own, purely subjective, esthetic criteria.

The next attractive stellation I found in this series is the 80th stellation. Unlike the 33rd, it is chiral.

And, after that, the 129th stellation, which is also chiral:

Next, the 152nd (and non-chiral) stellation:

I also found the non-chiral 158th stellation worthy of inclusion here:

After that, the chiral 171st stellation was the next one to attract my attention:

The next one to attract my notice was the also-chiral 204th stellation:

Some polyhedral stellation-series are incredibly long, with thousands, or even millions, of stellations possible before one reaches the final stellation, after which stellating the polyehdron one more time causes it to “wrap around” to the original polyhedron. Knowing this, I lost patience, and simply jumped straight to the final stellation of the rhombic triacontahedron — the last image in this post:

All of these images were created using Stella 4d: Polyhedron Navigator, a program available at http://www.software3d.com/Stella.php. For anyone interested in seriously studying polyhedra, I consider this program an indispensable research tool (and, no, I receive no compensation for all this free advertising for Stella which appears on my blog). There’s a free trial version available — why not give it a try?