I have made many posts here using polyhedral augmentation, but what I haven’t done — yet — is explain it. I have also neglected the reciprocal function of augmentation, which is called excavation. It is now time to fix both these problems.
Augmentation is the easier of the two to explain, especially with images. The figure below call be seen as a blue icosahedron augmented, on a single face, by a red-and-yellow icosidodecahedron. It can also be viewed, with equal validity, as the larger figure (the icosidodecahedron) augmented, on a single triangular face, with an icosahedron.
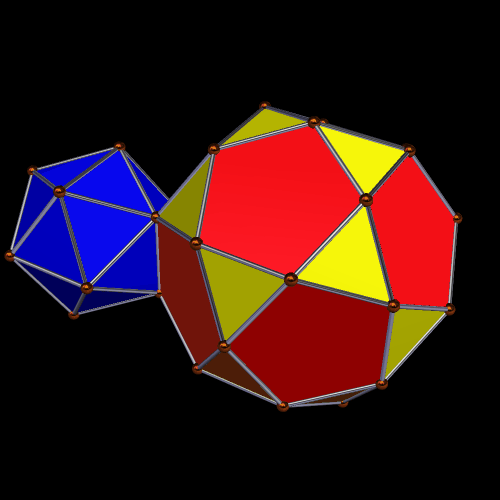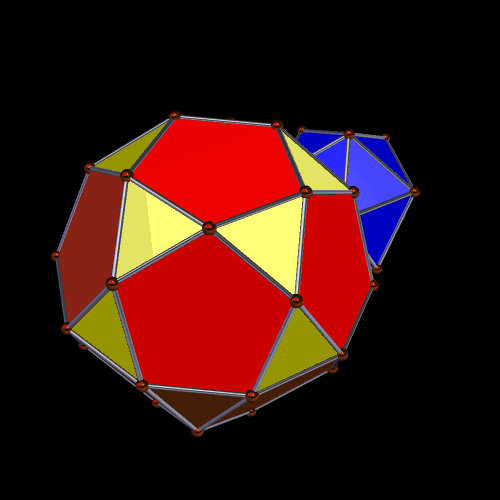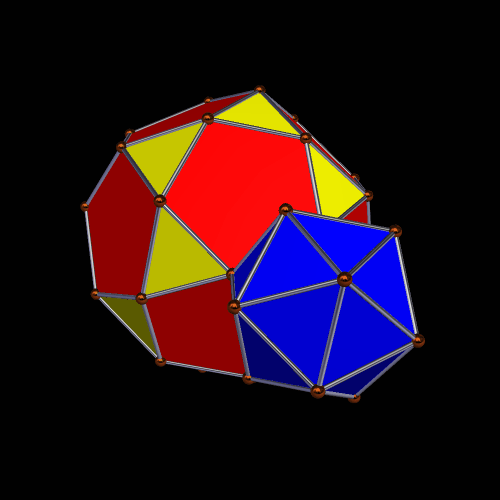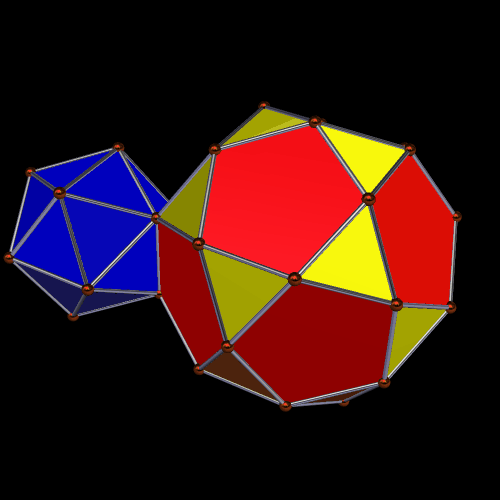
When augmenting an icosidodecahedron with an icosahedron in this manner, one simply attaches the icosahedron to a triangular face of the icosidodecahedron. The reciprocal process, excavation, involves “digging out” one polyhedral shape from the other. Here is what an icosidodecahedron looks like, after having an icosahedron excavated from it, on a single triangular face.

Excavating the smaller polyhedron from the larger one is easier to picture in advance, just as one can imagine what the Earth would look like, if a Moon-sized sphereoid were excavated from it, with a large, round hole making the excavation visible. (This is mathematics, not science, so we’re ignoring the fact that gravity would instantly cause the collapse of such a compound planetary object, with dire consequences for all inhabitants.) What’s more difficult is picturing what would result if this were turned around, and the Earth was used to excavate the Moon.
This “Earth-excavated Moon” idea is analogous to excavating the larger icosidodecahedron from the smaller icosahedron. If one thinks of subtracting the volume of one solid from that of the other, such a creature should have negative volume — except, of course, that this makes no sense, which is consistent with the fact that it would be impossible to do such a thing with physical objects: there isn’t enough matter in the Moon to remove an Earth’s worth of matter from the Moon. Also, moving back to polyhedra, with excavation only into a single face, it turns out that there is no change in appearance when the excavation-order is reversed:

(Well, OK, there was a small change in appearance between the two images, but that’s only because I changed the viewing angle a bit, to give you a better view of the blue faces.)
Things get different — and the augmentation- and excavation-orders begin to matter a lot more — when these operations are performed on all available faces at once, which, in this case, means on all twenty of each polyhedron’s triangular faces. Here is the easiest case to visualize: an icosidodecahedron, augmented by twenty icosahedra.

If you use the reciprocal function, excavation, but leave the order of polyhedra the same, you get a central icosidodecahedron, excavated by twenty smaller, intersecting icosahedra:
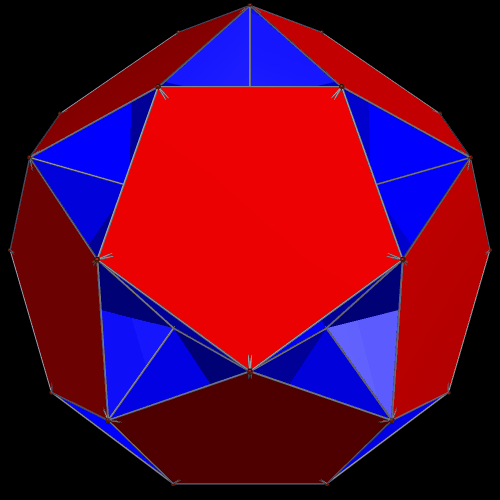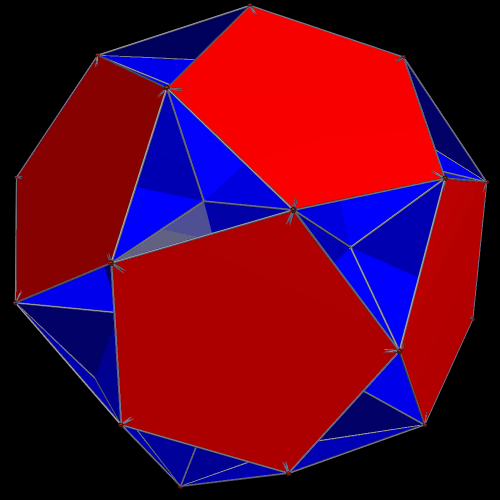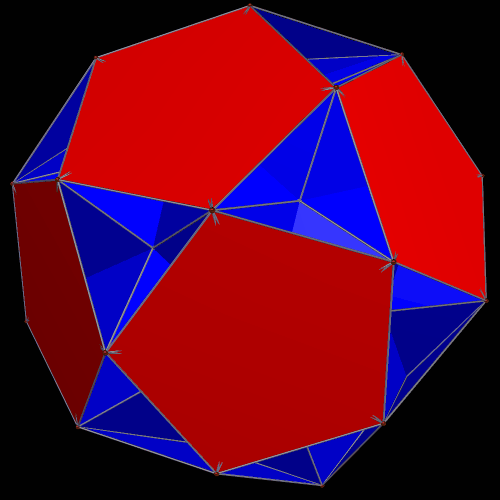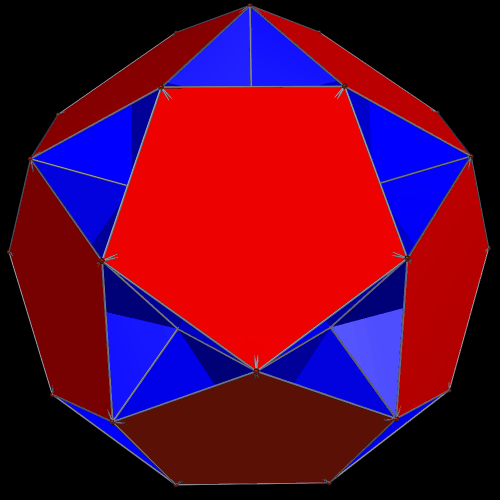
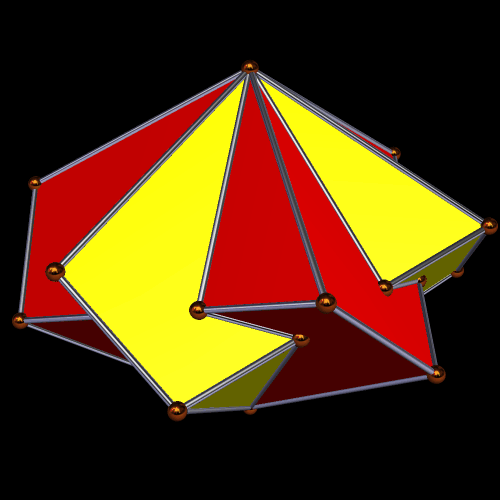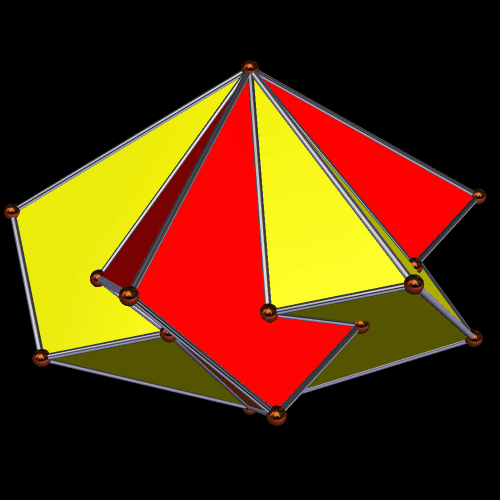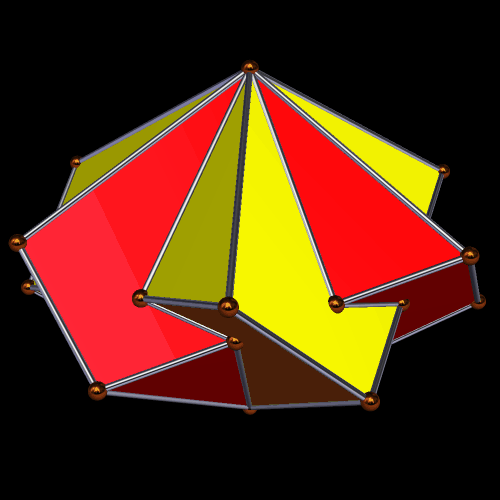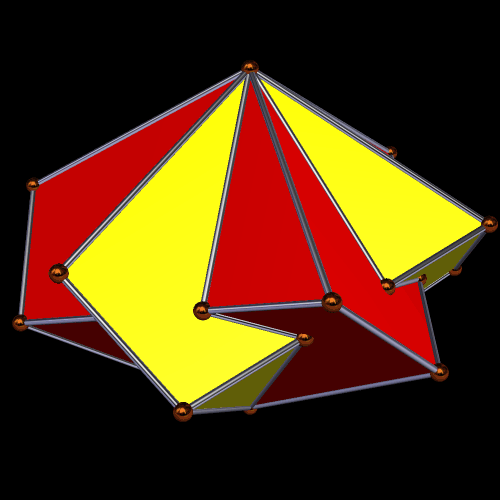
It is, of course, possible to have other combinations. The ones I find most interesting, using these two polyhedra, are “global” augmentation and excavation of the smaller figure, the icosahedron, by twenty of the larger ones, the icosidodecahedra. Why? Simple: putting the icosidodecahedra on the outside allows for maximum visibility of both pentagons and triangles. On the other hand, the central icosahedron is completely hidden from view, whether augmentation or excavation is used. Here is the augmentation case, or what I have called a “cluster” polyhedron, many varieties of which can be seen elsewhere on this blog (just search for “cluster,” or “cluster polyhedron,” to find them):

The global-excavation case which has the icosahedron hidden in the middle is similar to the cluster immediately above, in that all that can be seen are twenty intersecting icosidodecahedra. However, it also varies noticeably, because, with excavation, the icosidodecahedra are closer to the center of the entire cluster (the invisible, central icosahedron’s center) than was the case with augmentation. The last image here is of an invisible, central icosahedron, with an icosidodecahedron excavated from all twenty triangular faces. The larger polyhedra “punch through” the smaller one from all sides at once, trapping the central polyhedron — the blue icosahedron — from view. The remaining object looks, to me at least, more like a faceted icosidodecahedron than a cluster-polyhedron. I am of the opinion, but have not verified, that this resemblance to a faceting of the icosidodecahedron is illusory.

[Image credits: all images in this post were made using Stella 4d: Polyhedron Navigator. This program may be purchased, or tried as a free trial download, at http://www.software3d.com/Stella.php.]