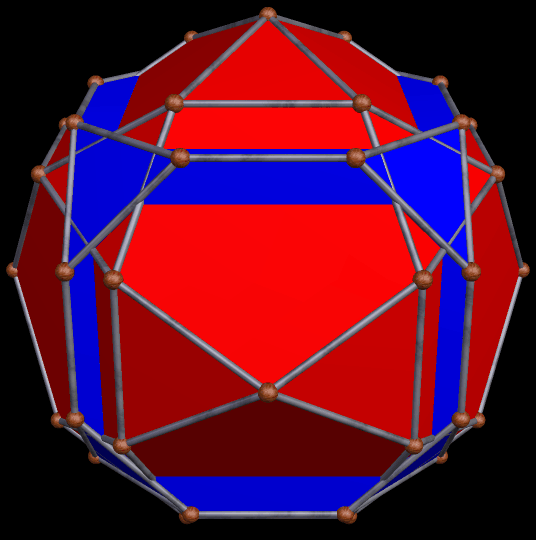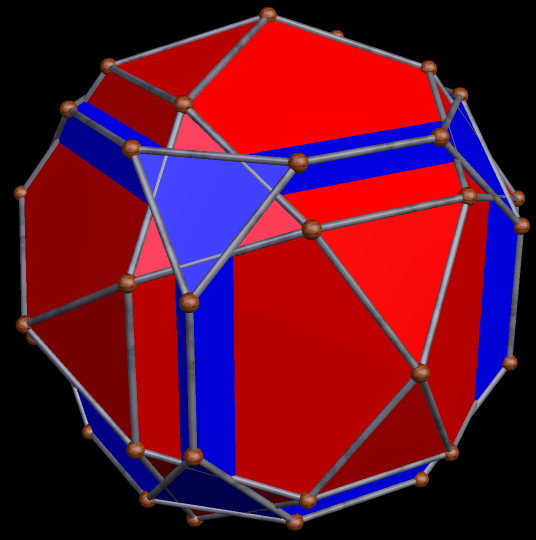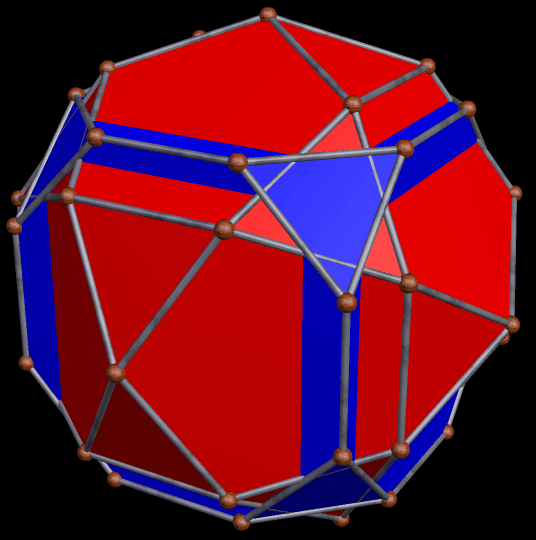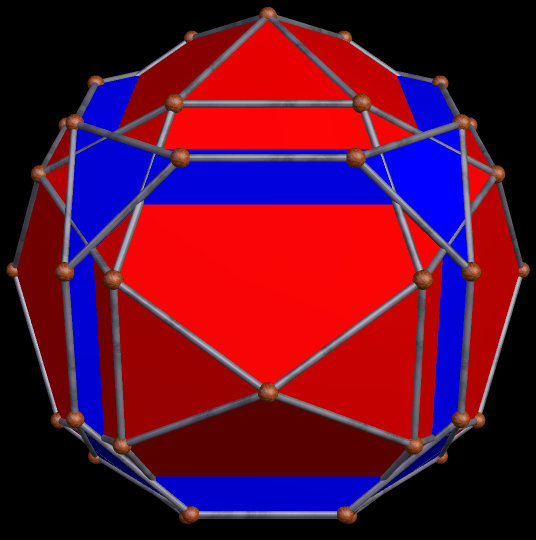
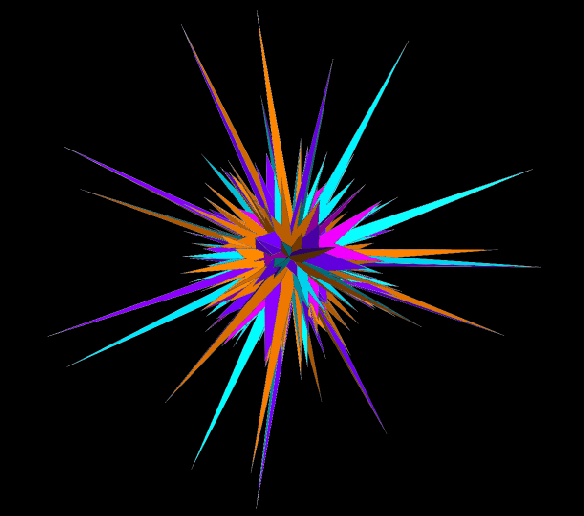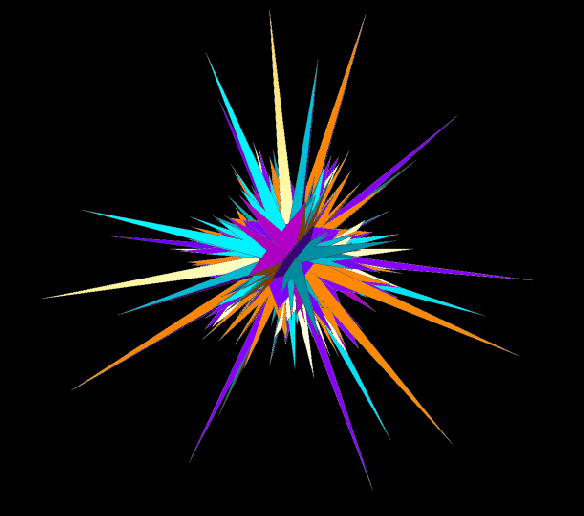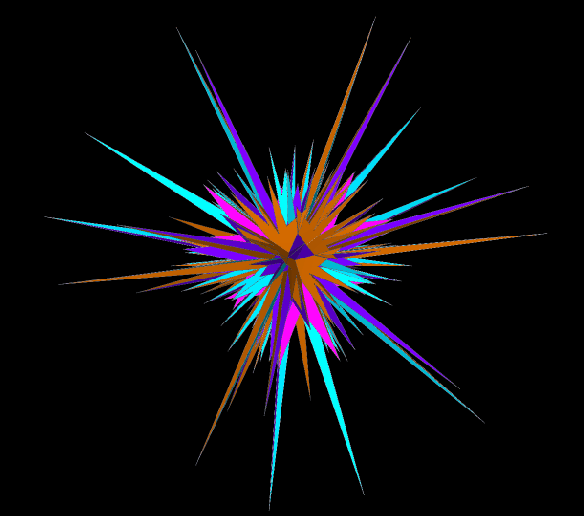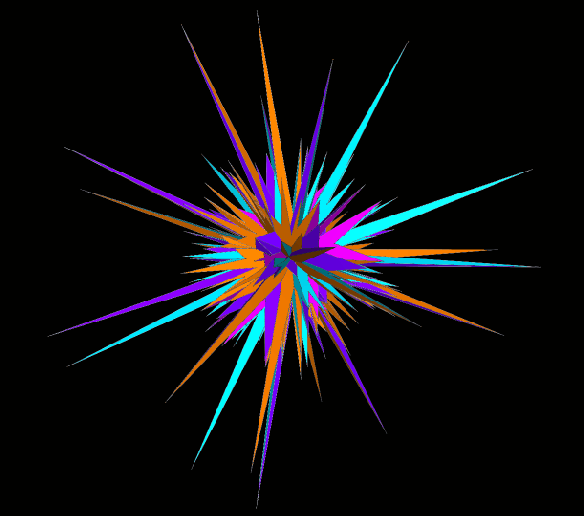
In the last post, several selections from the stellation-series of the great rhombicosidodecahedron (which some people call the truncated icosidodecahedron) were shown. It’s a long stellation-series — hundreds, or perhaps thousands, or even millions, of stellations long (I didn’t take the time to count them) — but it isn’t infinitely long. Eventually, if repeatedly stellating this polyhedron, one comes to what is called the “final stellation,” which looks like this:

Stellation-series “wrap around,” so if this is stellated one more time, the result is the (unstellated) great rhombicosidodecahedron. In other words, the series starts over.

The dual of the great rhombicosidodecahedron is called the disdyakis triacontahedron. The reciprocal function of stellation is faceting, so the dual of the figure above is a faceted disdyakis triacontahedron. Here is this dual:

To complicate matters further, there is more than one set of rules for stellation. For an explanation of this, I refer you to this Wikipedia page. In this post, and the one before, I am using what are known as the “fully supported” rules.

Both these images were made using Stella 4d, software you can buy, or try for free, right here. When stellating polyhedra using this program, it can be set to use different rules for stellation. I usually leave it set for the fully supported stellation criteria, but other polyhedron enthusiasts have other preferences.