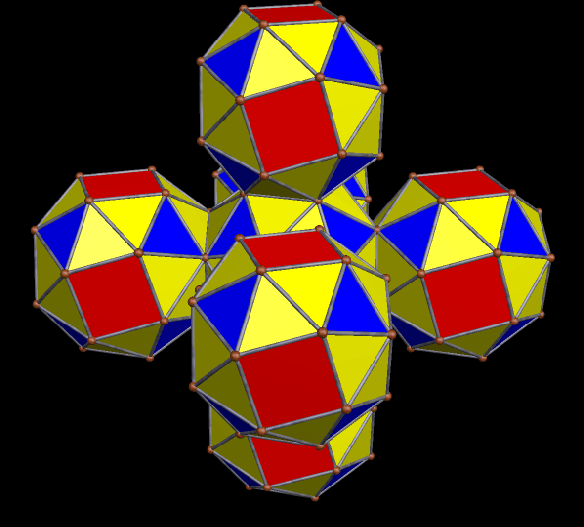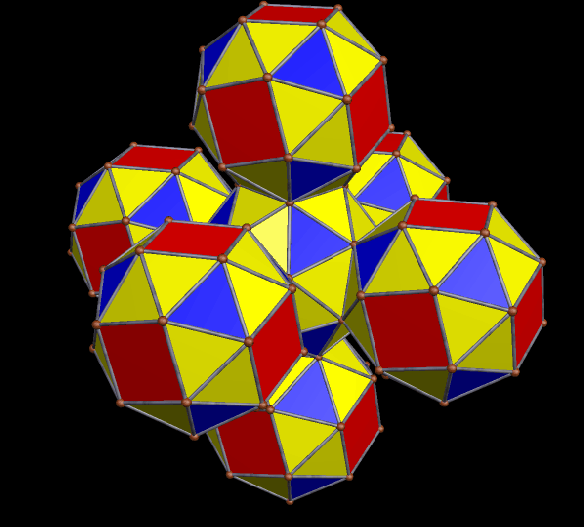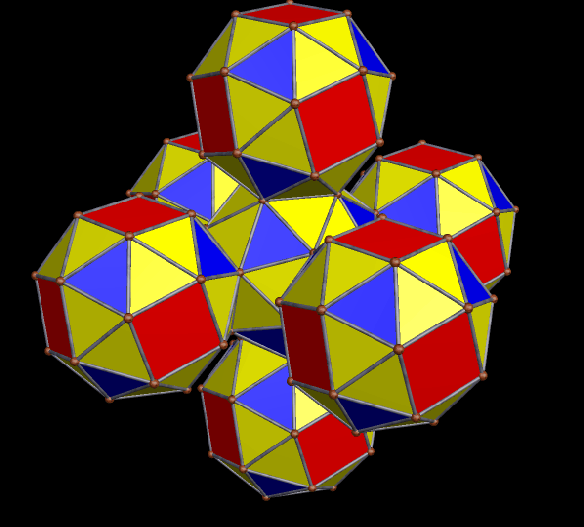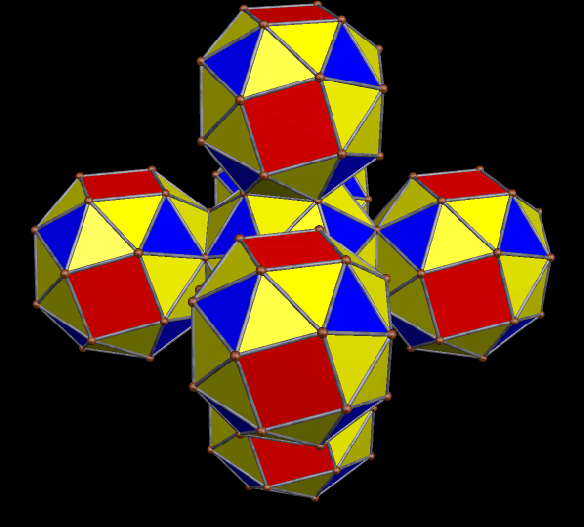
Created using Stella 4d, available here, by multiple stellations of a black icosidodecahedron, rendered as a rotating figure, against a black background.
Glimpses of the Invisible
1
Author Archives: RobertLovesPi
32 Octagonal Mandalas, Rotating in the Dark
To create the octagonal mandalas, I used Geometer’s Sketchpad and MS-Paint. I then projected them onto the faces of an all-but invisible icosidodecahedron, and created this rotating .gif image of it, using Stella 4d: Polyhedron Navigator, software you can try for free, right here.
A Dozen Octagonal Mandalas, Rotating in the Dark
To create the octagonal mandalas, I used Geometer’s Sketchpad and MS-Paint. I then projected them onto the faces of an all-but invisible dodecahedron, and created this rotating .gif image of it, using Stella 4d: Polyhedron Navigator, software you can try for free, right here.
Octagons
Rainbow Shamrock in Three Dimensions
Created using Stella 4d, which you can find at this website.
Sharp Impact
I made this using Stella 4d, which you can find here.
New “Near-Miss” Candidate?
As a proposed new “near-miss” to the Johnson solids, I created this polyhedron using Stella 4d, which can be found for purchase, or trial download, here. To make it, I started with a tetrahedron, augmented each face with icosidodecahedra, created the convex hull of the resulting cluster of polyhedra, and then used Stella‘s “try to make faces regular” function, which worked well. What you see is the result.
This polyhedron has no name as of yet (suggestions are welcome), but does have tetrahedral symmetry, and fifty faces. Of those faces, the eight blue triangles are regular, although the four dark blue triangles are ~2.3% larger by edge length, and ~4.6% larger by area, when compared to the four light blue triangles. The twelve yellow triangles are isosceles, with their bases (adjacent to the pink quadrilaterals) ~1.5% longer than their legs, which are each adjacent to one of the twelve red, regular pentagons. These yellow isosceles trapezoids have vertex angles measuring 61.0154º. The six pink quadrilaterals themselves are rectangles, but just barely, with their longer sides only ~0.3% longer than their shorter sides — the shorter sides being those adjacent to the green quadrilaterals.
The twelve green quadrilaterals are trapezoids, and are the most irregular of the faces in this near-miss candidate. These trapezoids have ~90.992º base angles next to the light blue triangles, and ~89.008º angles next to the pink triangles. Their shortest side is the base shared with light blue triangles. The legs of these trapezoids are ~2.3% longer than this short base, and the long base is ~3.5% longer than the short base.
If this has been found before, I don’t know about it — but, if you do, please let me know in a comment.
UPDATE: It turns out that this polyhedron has, in fact, been found before. It’s called the “tetrahedrally expanded tetrated dodecahedron,” and is the second polyhedron shown on this page. I still don’t know who discovered it, but at least I did gather more information about it — the statistics which appear above, as well as a method for constructing it with Stella.
A Faceting of the Truncated Dodecahedron, Together with Its Dual
This faceting of the truncated dodecahedron, one of many, was made with Stella 4d, software you can buy, or try for free, here. Here is its dual, below.
Albert Einstein, on Morality
On Consistent and Inconsistent Combining of Chiralities, Using Polyhedral Augmentation
For any given chiral polyhedron, a way already exists to combine it with its own mirror-image — by creating a compound. However, using augmentation, rather than compounding, opens up new possibilities.
The most well-known chiral polyhedron is the snub cube. This reflection of it will be referred to here using the letter “A.”
To avoid unnecessary confusion, the same direction of rotation is used throughout this post. Apart from that, though, the image below, “Snub Cube B,” is the reflection of the first snub cube shown.
There are many ways to modify polyhedra, and one of them is augmentation. One way to augment a snub cube is to attach additional snub cubes to each square face of a central snub cube, creating a cluster of seven snub cubes. In the next image, all seven are of the “A” variety.
If one examines the reflection of this cluster of seven “A” snub cubes, all seven, in the reflection, are of the “B” variety, as shown here:
Even though one is the reflection of the other, both clusters of seven snub cubes above have something in common: consistent chirality. As the next image shows, inconsistent chirality is also possible.
The cluster shown immediately above has a central snub cube of the “A” variety, but is augmented with six “B”-variety snub cubes. It therefore exhibits inconsistent chirality, as does its reflection, a “B” snub cube augmented with “A” snub cubes:
With simple seven-part snub-cube clusters formed by augmentation of a central snub cube’s square faces by six snub cubes of identical chirality to each other, this exhausts the four possibilities. However, multiplying the possibilities would be easy, by adding more components, using other polyhedra, mixing chiralities within the set of polyhedra added during an augmentation, and/or mixing consistent and inconsistent chirality, at different stages of the growth of a polyhedral cluster formed via repeated augmentation.
All the images in this post were created using Stella 4d, which you can try for yourself at this website.
RobertLovesPi.net 