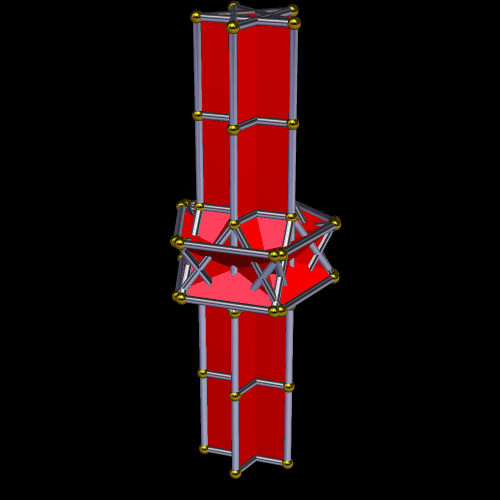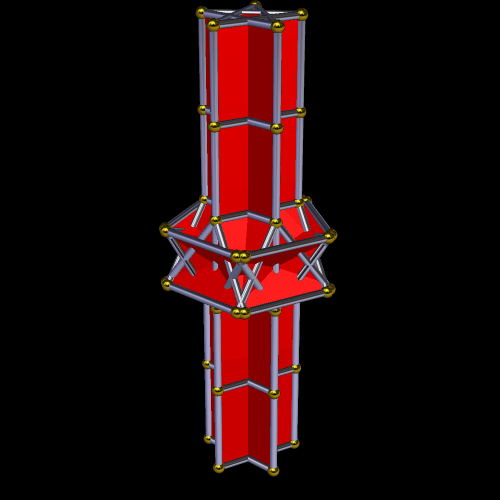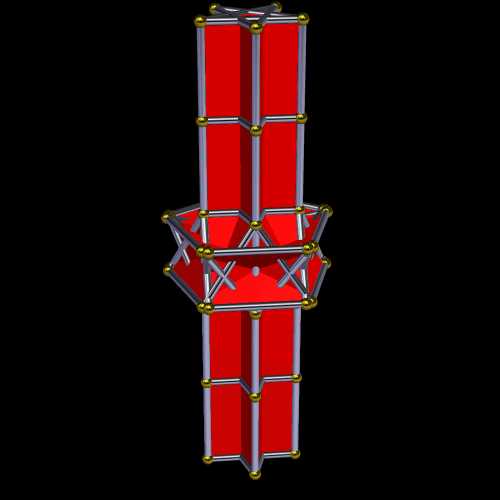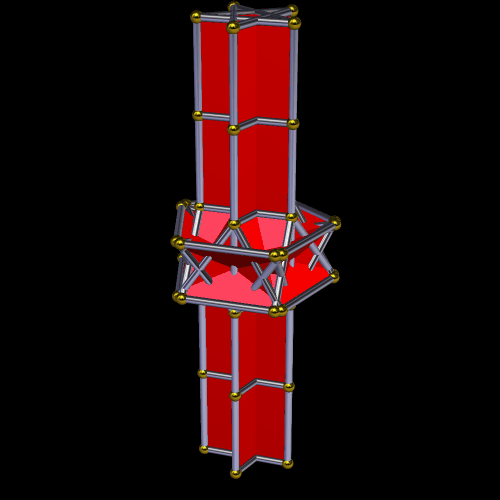
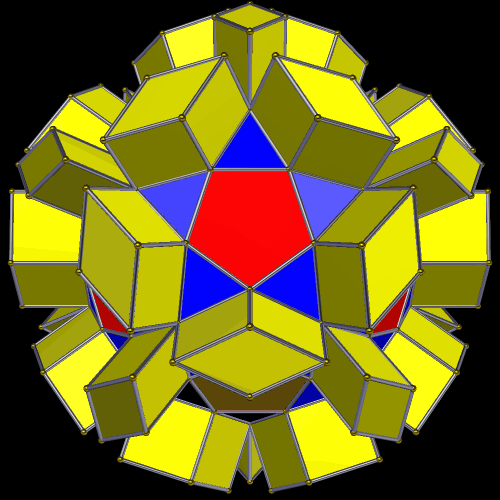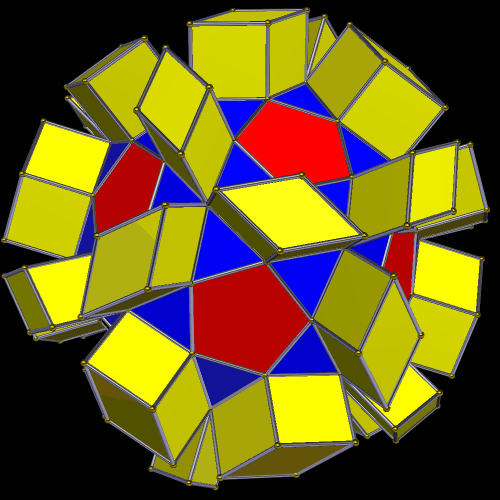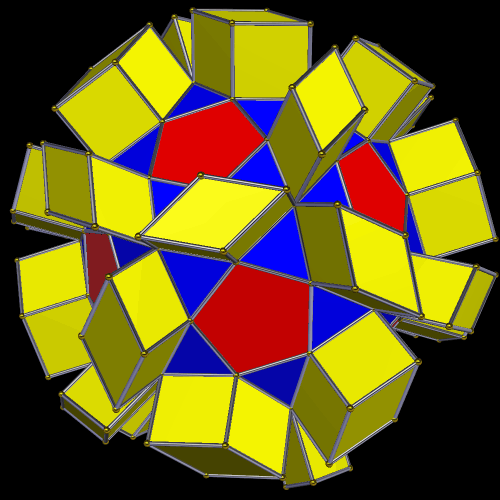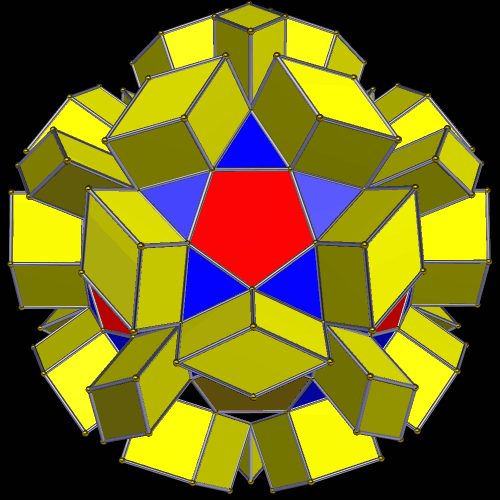
This symmetrohedron has eight hexagonal faces, six square faces, and twelve pairs of trapezoids, for a total of 38 faces. I made it by using Stella 4d to modify a truncated octahedron. You may try this program for free at www.software3d.com/Stella.php.
I made this using Stella 4d, which you can try for free right here.
This 122-faced solid is the dual of the convex hull of the compound of the rhombicosidodecahedron and its dual, the strombic hexecontahedron. Its regular faces are 20 triangles, 12 pentagons, and 30 squares. It also has 60 faces which are isosceles trapezoids.
I made this using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.
Each ring contains 14 heptagons. Here’s another coloring of it:
This is a projection of a rotating duoprism, a four-dimensional figure, with bases which are all star pentagons. This polytope’s faces include ten of these pentagrams, and twenty-five squares. Its three-dimensional cells are ten pentagrammic prisms. I made it using Stella 4d, a program which you can try, for free, at http://www.software3d.com/Stella.php. Here is this duoprism’s three-dimensional net.
This is the compound of five dodecahedra, a shape which is included in the built-in polyhedral library of Stella 4d, a program you can try for yourself, free, right here.
I wanted to see what I could make, starting from this compound. My first modification to it was to create its convex hull, which is shown below.
The next move was to use Stella‘s “Try to Make Faces Regular” function, which produced this:
Next, I augmented this figure’s thirty yellow rhombi with prisms.
I then created the convex hull of this augmented polyhedron.
Next, I used the “Try to Make Faces Regular” function again, producing a solid that looks, to me, like a hybrid of the rhombicosidodecahedron and the rhombic triacontahedron.
This polyhedron has yellow faces that are almost squares. Careful inspection reveals that they are actually isosceles trapezoids. The next thing I did was to augment each of these trapezoids with a tall prism.
The next step was to, again, create the convex hull.
That was the end of this polyhedral journey, but I am confident there will be others.
RobertLovesPi.net 