Monday’s Holiday

Posted on 6 October 2023 by RobertLovesPi

Banks, the U.S. bond market, and the U.S. Post Office will all be closed on John Lennon’s birthday this year (Monday, October 9th).

A Pair of Polyhedra Derived From the Snub Archimedeans

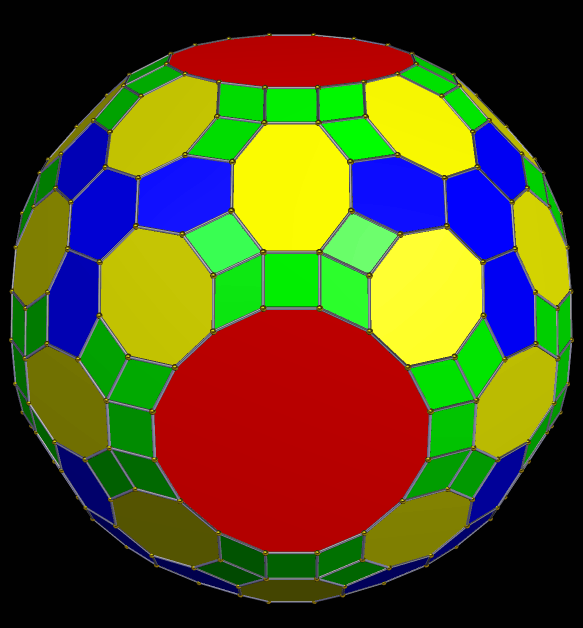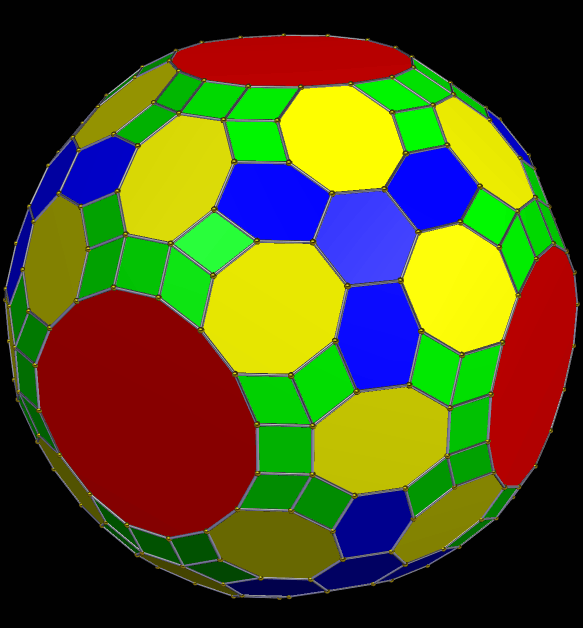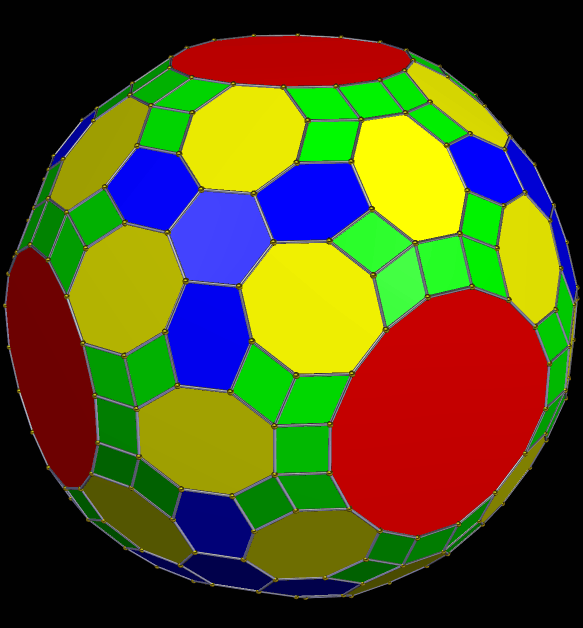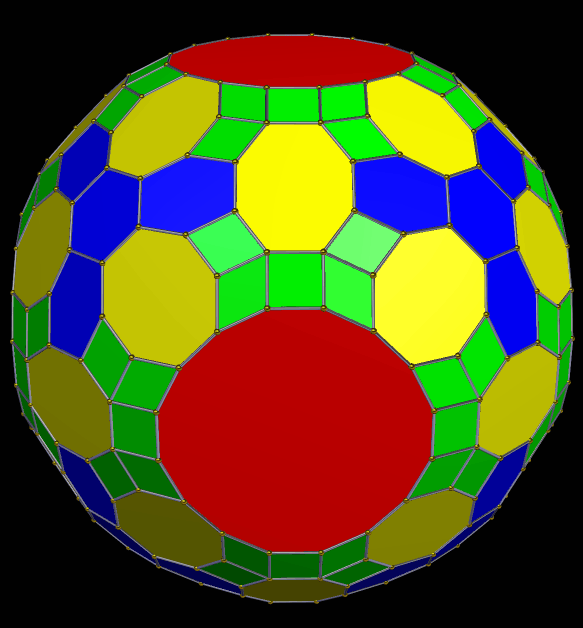
Posted on 4 October 2023 by RobertLovesPi

To make the polyhedron shown above, I started with a snub cube, then augmented all the triangular faces with prisms. Next, I formed this augmented solid’s convex hull, and, finally, I used the “try to make faces regular” function of the software I use to manipulate polyhedra (Stella 4d, which you can try here). The regular faces are the octagons and the small triangles.

I used the same process to make the polyhedron below, except that I started with the snub dodecahedron.

Clusters of Rhombic Triacontahedra

Posted on 2 October 2023 by RobertLovesPi

Here’s a rhombic triacontahedron, possibly the most well-known of the Catalan solids. It’s thirty faces are all golden rhombi (rhombi with their diagonals in the golden ratio).

Here’s what you get if you augment each face with another rhombic triacontahedron:

Coloring this cluster-polyhedron by face type has this result:

So what happens if each face of this cluster-polyhedron is augmented by another rhombic triacontahedron? This does:

Here’s another view of that, in “rainbow color mode”:

I made these virtual models with Stella 4d: Polyhedron Navigator. If you’d like to try this software for free, the website to visit is http://www.software3d.com/Stella.php.

Four Interpenetrating Regular Hexagons

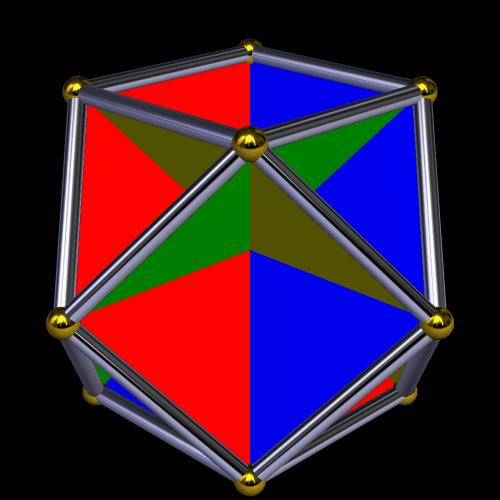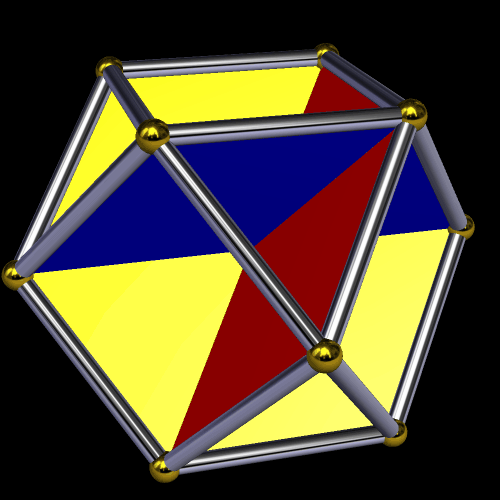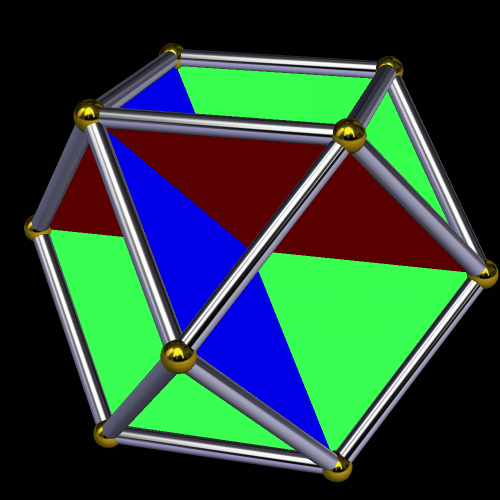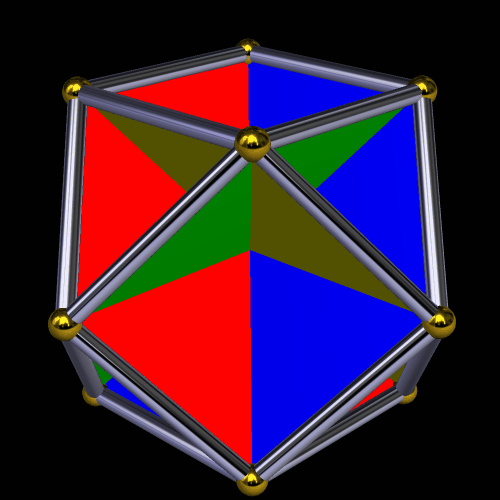
Posted on 22 September 2023 by RobertLovesPi

To make the image above, using Stella 4d (available here), I started with a uniform polyhedron called the octahemioctahedron, and then made the triangular faces of it invisible. Here’s what this polyhedron looks like without its triangles hidden:

The convex hull of either of these figures is a cuboctahedron, which is shown below.

Six Interpenetrating Regular Decagons

Posted on 21 September 2023 by RobertLovesPi

To make the image above, using Stella 4d (available here), I started with a uniform polyhedron called the small icosihemidodecahedron, and then made the triangular faces of it invisible. Here’s what this polyhedron looks like without its triangles hidden:

The convex hull of either of these figures is an icosidodecahedron, which is shown below.

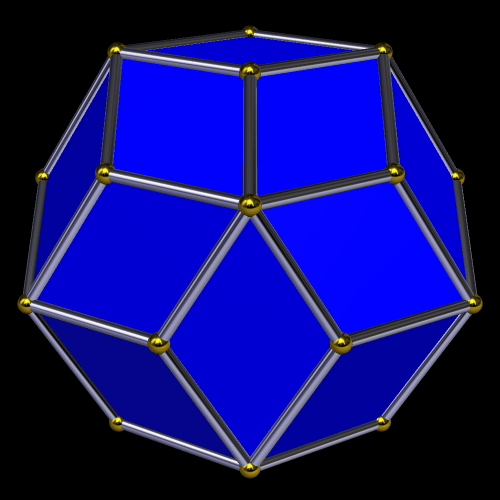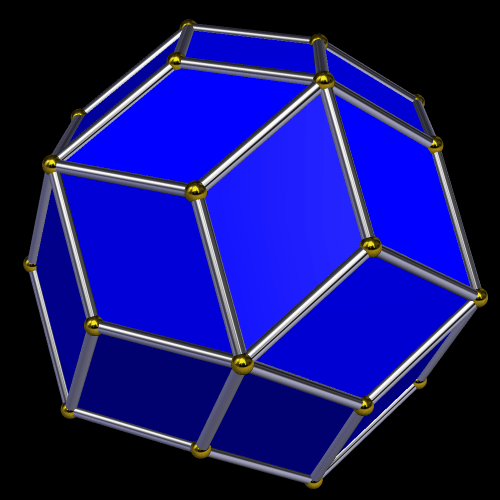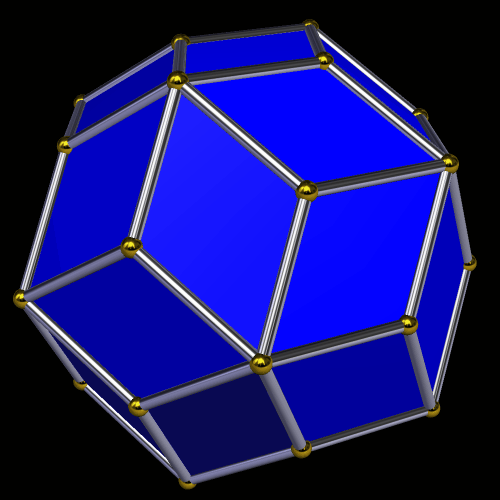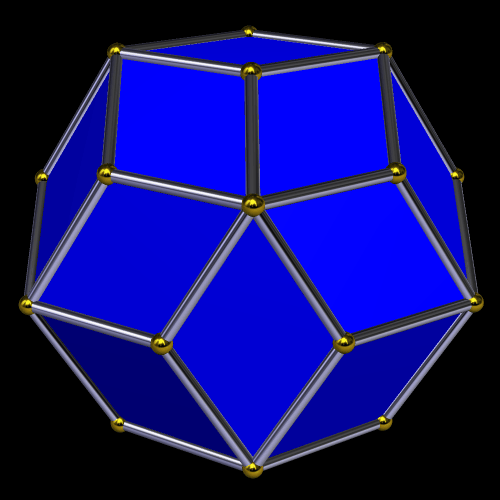
A Zonohedron Derived From the Truncated Octahedron

Posted on 20 September 2023 by RobertLovesPi

This zonohedron is made from the truncated octahedron’s vertices, edges, and faces. I made it using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Cluster of Fifteen Cuboctahedra

Posted on 14 September 2023 by RobertLovesPi

There’s one cuboctahedron in the center of this cluster, with each of its fourteen faces augmented by another cuboctahedron. The image below uses coloring of each face by its number of sides, while the next one is in “rainbow color mode.”

I made these images using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Compound of a Strombic Icositetrahedron and the Rhombic Dodecahedron

Posted on 13 September 2023 by RobertLovesPi

I made this using Stella 4d, which you can try for yourself, free, at this website: http://www.software3d.com/Stella.php.

A Four-Part Polyhedral Compound Derived From the Small Cubicuboctahedron

Posted on 12 September 2023 by RobertLovesPi

I found this compound by repeatedly stellating the small hexacronic icositetrahedron, which is the dual of the small cubicuboctahedron, one of the uniform solids. I used Stella 4d: Polyhedron Navigator to do this, and you can try this program, as a free trial download, at http://www.software3d.com/Stella.php.