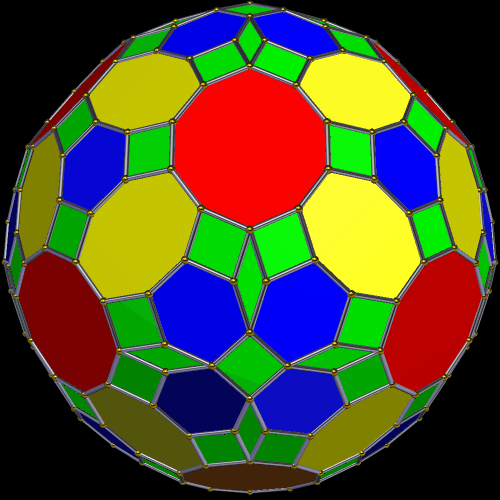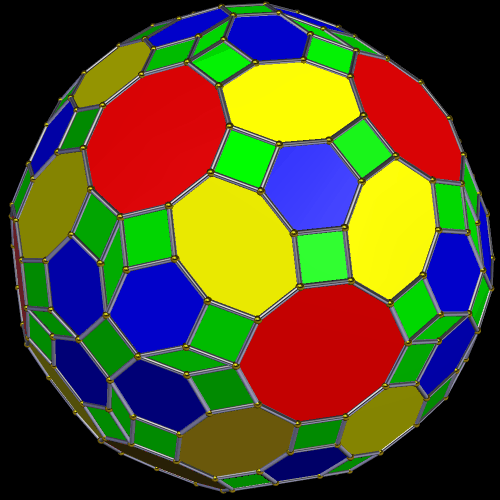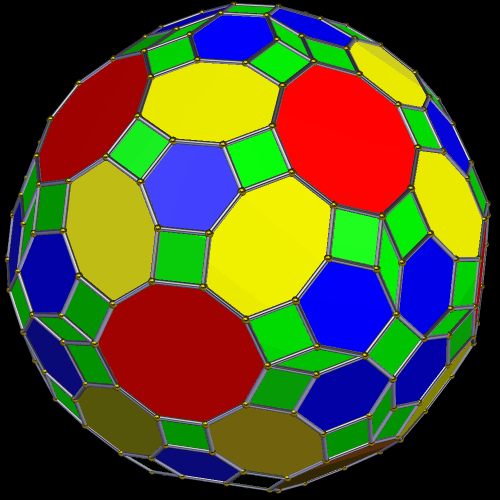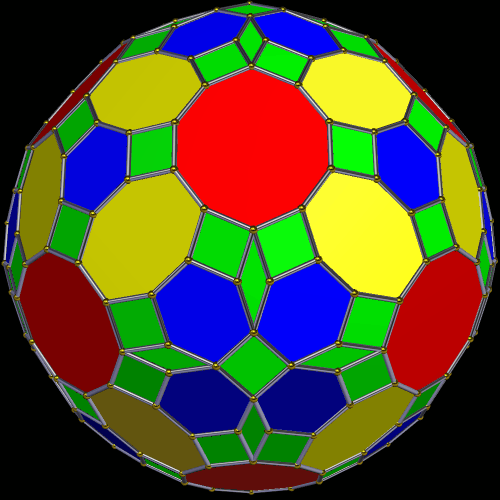
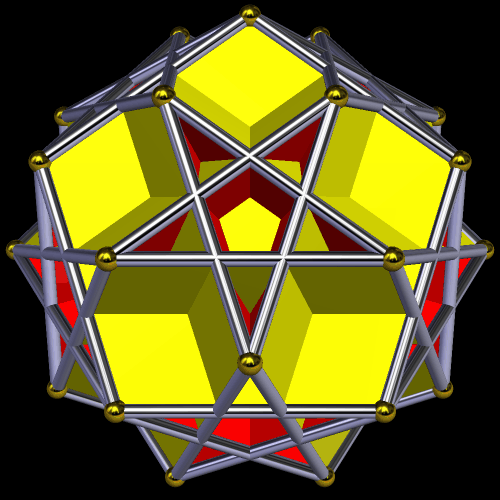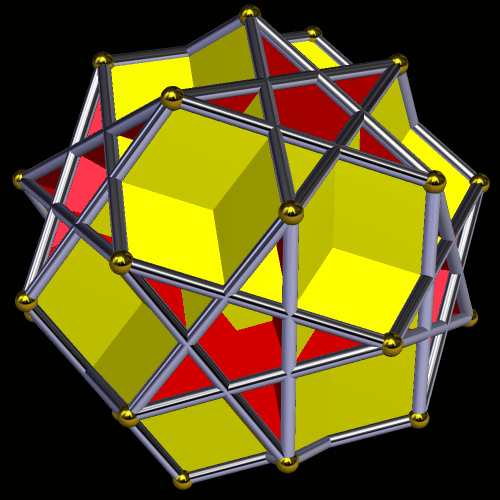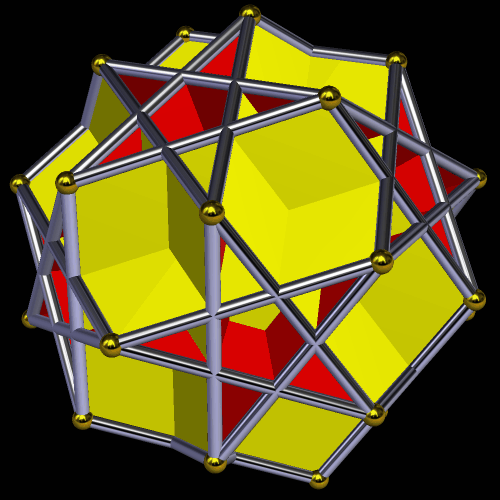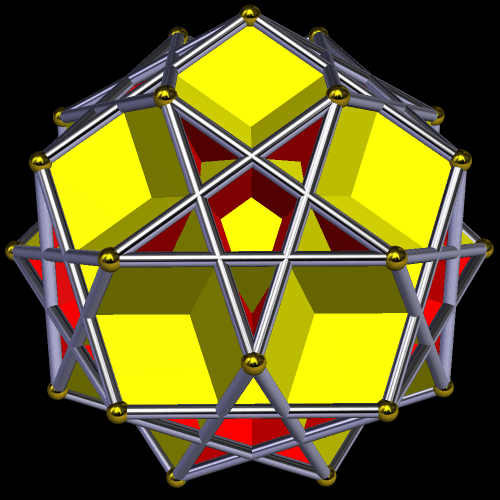
I made this polyhedron, which has 170 faces, using Stella 4d: Polyhedron Navigator. You may try this program, for free, at http://www.software3d.com/Stella.php.
A Zonohedron Based on the Faces, Edges, and Vertices of a Truncated Tetrahedron
I made this model using Stella 4d, which you can try for free at this website.
A Three-Component Compound
I made this compound using Stella 4d, which you can try for yourself right here.
A Polyhedron With 152 Faces, and Icosidodecahedral Symmetry
I made this solid using Stella 4d: Polyhedron Navigator. You can try this program for free at http://www.softwared.com/Stella.php.
The Octahemioctahedron, and Three Views of Its First Stellation
This is the octahemioctahedron, which is one of the uniform polyhedra. It has twelve faces: eight equilateral triangles, and four regular hexagons. The hexagons pass through the center of the polyhedron.
Here’s the first stellation of this polyhedron, colored by face type.
Here’s a second view of this first stellation, colored by face, with parallel faces given the same color.
Finally, here’s this first stellation in “rainbow color mode.”
I used Stella 4d: Polyhedron Navigator to make these images. You can try this program for free at http://www.software3d.com/Stella.php.
The Great Dodecahemiicosahedron, With Two of Its Stellations
Recently (here and here), I blogged about the small dodecahemiicosahedron, along with several of its stellations. Today, I got curious about it’s “big brother,” the great dodecahemiicosahedron, so I looked up the latter with Stella 4d (free trial download available here), examined some of its stellations, and made virtual models of what I found.
First, the great dodecahemiicosahedron itself. The 22 faces of this uniform polyhedron are twelve regular pentagons (shown in yellow) and twenty regular hexagons (shown in red).
Next, its 30th stellation:
Lastly, the 88th stellation:
When creating polyhedral models, I usually use gold spheres for vertices, and silver cylinders for edges. However, in this case, that decoration is getting in the way — so here’s the 88th stellation again, without the spheres and cylinders. This way, it really looks like what it is: a dozen tall pentagonal pyramids meeting only at their common vertex.
Some Pictures of Today’s Partial Solar Eclipse
This is how today’s eclipse of the sun looked in Maumelle, Arkansas, USA, with solar viewing sunglasses held over my cell phone camera. The camera is set on maximum magnification (x10).
Next, here’s a shot of a shadow of a tree, along with another of the tree itself. Can you see the solar crescents on the street?
It’s hard to aim a cell phone camera at the sun while holding eclipse-viewing sunglasses over the lens. For some shots, I didn’t have the sunglasses positioned correctly, resulting in images like this. These shots show a whited-out sun, along with some sort of internal reflection which produced a dimmed-down mirror-image of the eclipsed sun. They appear below, with varying degrees of cropping.

More Stellations of the Small Dodecahemiicosahedron
In the last post here, I showed off the small dodecahemiicosahedron, along with three of its stellations. I’ve now had time to take a deeper dive into this stellation-series, and I found several more stellations to share. First, the 32nd stellation.
Next, the 38th stellation.
The 40th stellation also caught my eye.
Finally, here’s the 51st stellation of this uniform solid.
I made these models using Stella 4d: Polyhedron Navigator, and you can try this program for yourself, free, at http://www.software3d.com/Stella.php.
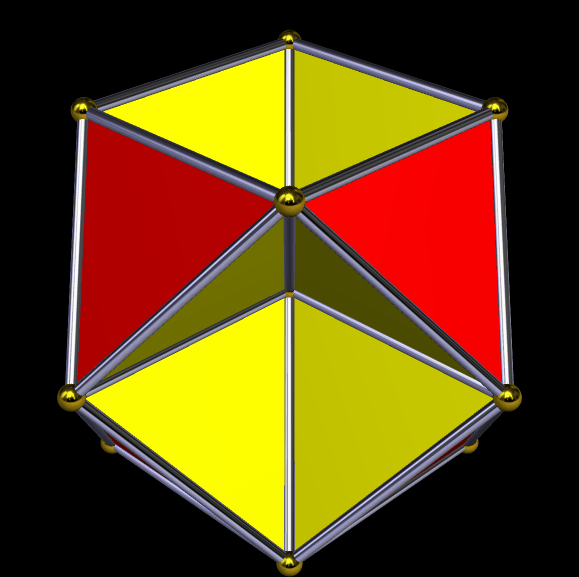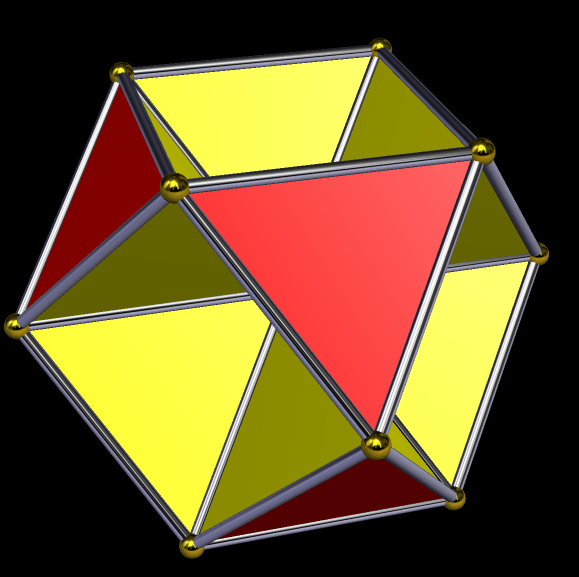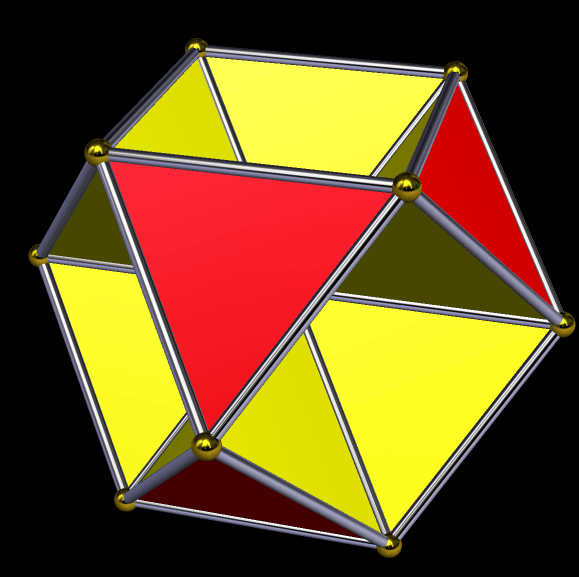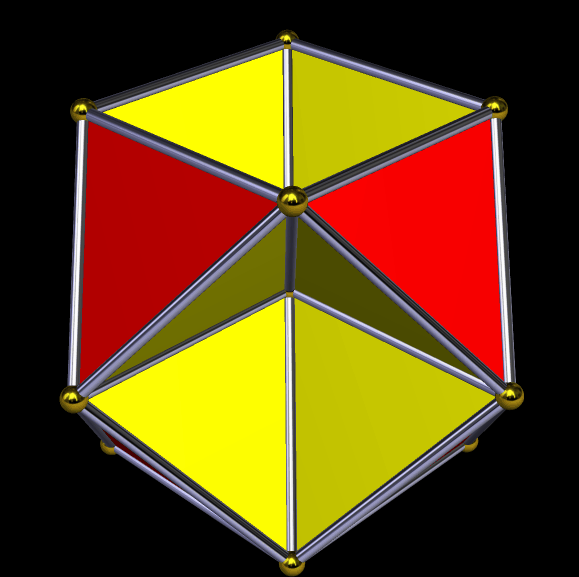
The Small Dodecahemiicosahedron, and Three of Its Stellations
Here’s the small dodecahemiicosahedron, which is one of the uniform polyhedra. It has 22 faces: the twelve star pentagons shown in red, and the ten regular hexagons shown in yellow.
This solid has a long and interesting stellation-series. Three excerpts from that series are shown below. First, the tenth stellation.
Next, the eighteenth stellation.
Finally, the thirtieth stellation.
I made these .gifs using Stella 4d: Polyhedron Navigator, which you can try for free at http://www.software3d.com/Stella.php.
A Pair of Symmetrohedra Derived From the Rhombicosidodecahedron
To make this first symmetrohedron, I started with the rhombicosidodecahedron, augmented its thirty square faces with antiprisms, and then formed the convex hull of that solid. (I did all of this using Stella 34d: Polyhedron Navigator, which you can try for free right here.) The resulting polyhedron contains, as faces, twelve regular pentagons, twenty equilateral triangles, thirty squares, and sixty isosceles trapezoids, or 122 faces in all.
Next, I applied Stella’s “try to make faces regular” function, which produced the solid seen below. This had the effect of transforming the squares into rhombi, and changing the trapezoids so that, while still isosceles trapezoids, they closely resemble squares.