Above and below, you will find two different coloring-schemes for this particular cluster of polyhedra. I made both of these rotating images using Stella 4d, software you can buy, or try for free, right here.
Tag Archives: cluster
A Central Icosahedron, Augmented with Twenty Rhombicosidodecahedra
A model this complex would have taken days to build by hand. With software called Stella 4d: Polyhedron Navigator, however, making this “virtual model” was easy. This program is available for purchase at this website — and there is a free trial download available there, as well.
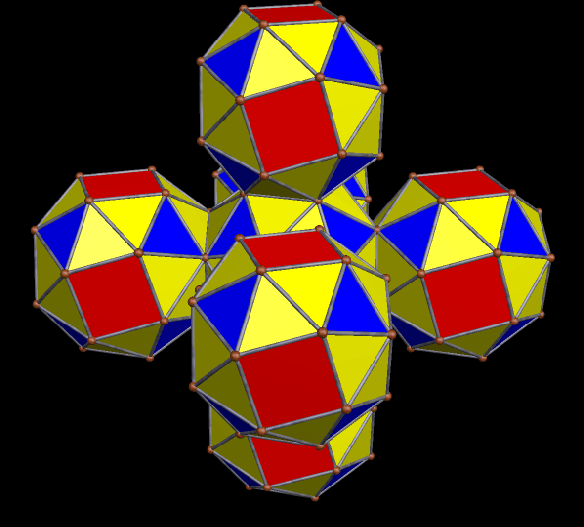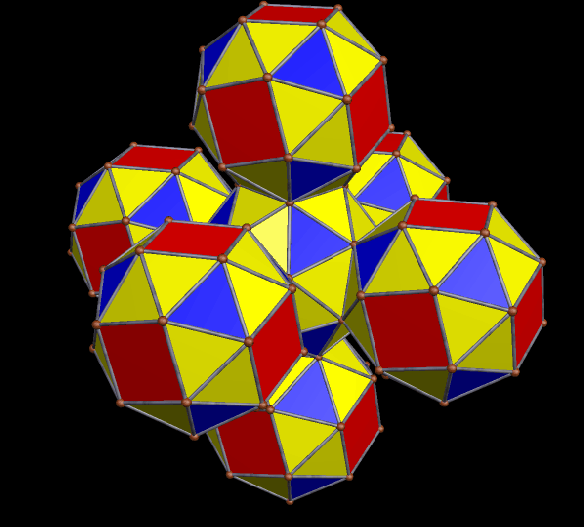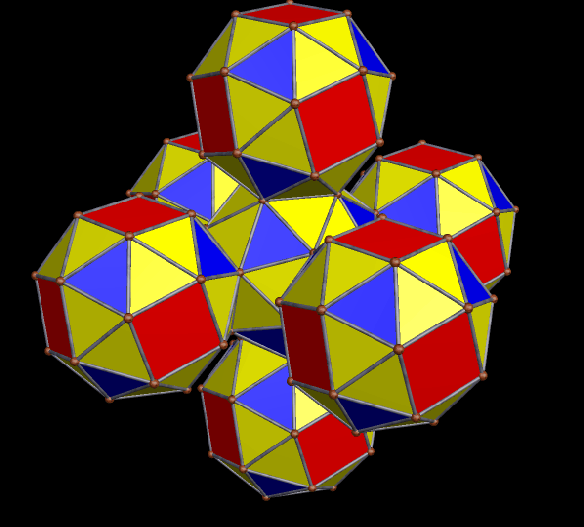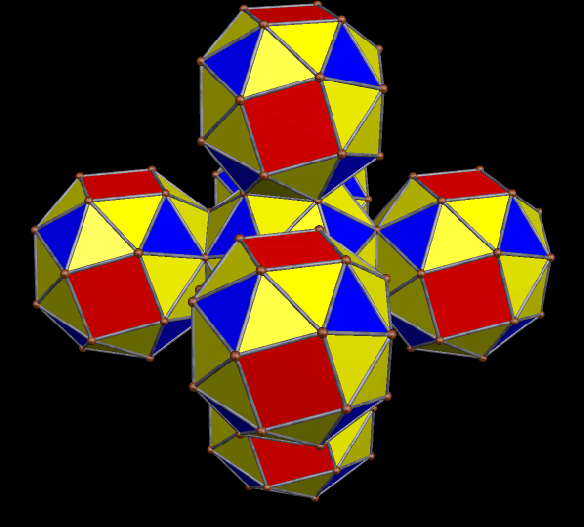
Five More Clusters of Rhombicosidodecahedra
Making the four different clusters of rhombicosidodecahedra seen in the post right before this one was fun, so I decided to make more of them.
There are two different forms of the compound of twenty tetrahedra. To make the polyhedral cluster above, I chose one of them, and then augmented each of its 20(4) = 80 triangular faces with a rhombicosidodecahedron.
For the next of these clusters, I decided to move away from using compounds for the central, hidden figure. Instead, I chose a snub cube, and augmented each of its 32 triangular faces with a rhombicosidodecahedron. Since the snub cube is chiral, this cluster is chiral as well.
Any chiral polyhedron can be combined with its mirror-image to produce a new compound, and that’s what I did to make this next cluster, which is composed of 64 rhombicosidodecahedra: I simply added the cluster above to its own reflection.
Next, I turned to the snub dodecahedron, also chiral, and with 80 triangular faces. Augmentation of all 80 produced this chiral cluster of 80 rhombicosidodecahedra:
Finally, I added this last cluster to its own mirror-image, producing this symmetrical cluster of 160 rhombicosidodecahedra.
Each of these was created using a program called Stella 4d: Polyhedron Navigator, software you can try for free right here.
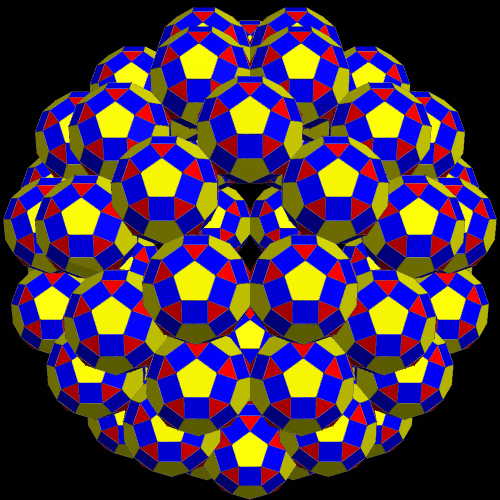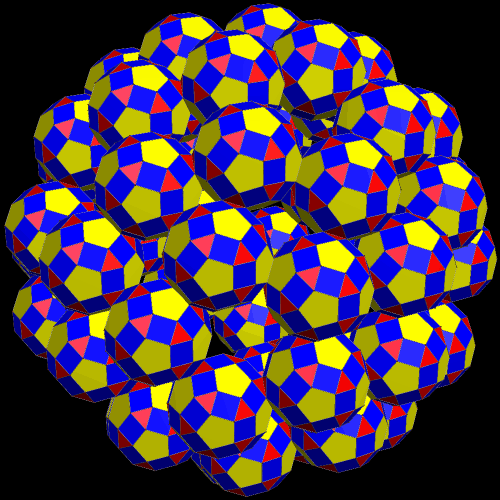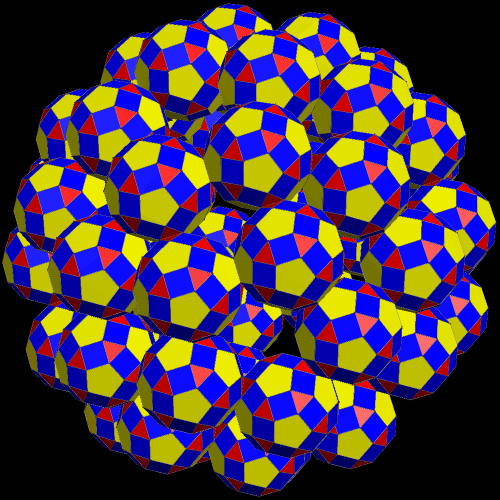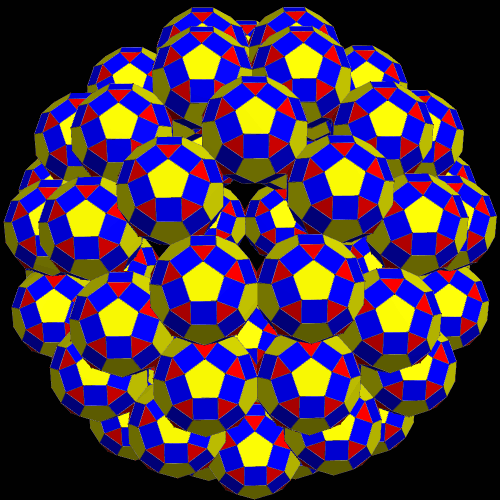
Four Different Clusters of Multiple Rhombicosidodecahedra
To make the cluster above, I began with the compound of five octahedra, which has 5(8) = 40 faces, all of them equilateral triangles. Next, I augmented each of those triangular faces with a single rhombicosidodecahedron — forty in all.
Next, I started anew with the compound of five dodecahedra, which has 5(12) = 60 pentagonal faces, all of them regular. Each of these sixty pentagons was then augmented by a single rhombicosidodecahedron.
For the next cluster, I started with the most well-known compound of ten tetrahedra. There are actually two such compounds; I used the one which is the compound of the chiral five-tetrahedron compound, combined with its mirror image. Since 10(4) = 40, this cluster, like the first one in this post, contains forty rhombicosidodecahedra. Unlike the other models shown here, this one has “holes,” which you can see as it rotates, but the reason for this is a mystery to me. The same is true for the first cluster shown in this post.
There also exist two compounds of eight tetrahedra each, and I used one of them for this next cluster, using the same procedure, so this cluster is composed of 8(4) = 32 rhombicosidodecahedra.
All four of these clusters were created with Stella 4d, a program you may try for free here.
The Great Rhombicosidodecahedron, Built from Rhombic Triacontahedra, and Its Dual
The great rhombicosidodecahedron is also known as the truncated icosidodecahedron (and, confusingly, several other names). Regardless of what it’s called, these pictures demonstrate that this Archimedean solid can be constructed using rhombic triacontahedra as building-blocks.
First, here’s one in the same color I used for the decagonal ring of rhombic triacontahedra in the last post:
The next one is identical, except I used “rainbow color mode” for it.
Also, just in case you’re curious, here’s the dual of this polyhedron-made-of-polyhedra — this time, colored by face-type.
These virtual models were all built using Stella 4d, software you may buy, or try for free, right here.
A Cluster of Twenty Great Icosahedra, Excavated from the Faces of a Central Icosahedron, Along with Its Dual
These twenty great icosahedra were excavated from the faces of a central icosahedron, which is concealed in the figure’s center. These excavations exceed the limits of the central icosahedron, resulting in each great icosahedron protruding in a direction opposite that of the face from which it is excavated. In a certain sense, then, the figure above has negative volume.
To make this, I used software called Stella 4d: Polyhedron Navigator. It can be researched, bought, or tried for free here.
Also, here is the dual of the polyhedral cluster above, made with the same program.
On Consistent and Inconsistent Combining of Chiralities, Using Polyhedral Augmentation
For any given chiral polyhedron, a way already exists to combine it with its own mirror-image — by creating a compound. However, using augmentation, rather than compounding, opens up new possibilities.
The most well-known chiral polyhedron is the snub cube. This reflection of it will be referred to here using the letter “A.”
 To avoid unnecessary confusion, the same direction of rotation is used throughout this post. Apart from that, though, the image below, “Snub Cube B,” is the reflection of the first snub cube shown.
To avoid unnecessary confusion, the same direction of rotation is used throughout this post. Apart from that, though, the image below, “Snub Cube B,” is the reflection of the first snub cube shown.
There are many ways to modify polyhedra, and one of them is augmentation. One way to augment a snub cube is to attach additional snub cubes to each square face of a central snub cube, creating a cluster of seven snub cubes. In the next image, all seven are of the “A” variety.
If one examines the reflection of this cluster of seven “A” snub cubes, all seven, in the reflection, are of the “B” variety, as shown here:
Even though one is the reflection of the other, both clusters of seven snub cubes above have something in common: consistent chirality. As the next image shows, inconsistent chirality is also possible.
The cluster shown immediately above has a central snub cube of the “A” variety, but is augmented with six “B”-variety snub cubes. It therefore exhibits inconsistent chirality, as does its reflection, a “B” snub cube augmented with “A” snub cubes:
With simple seven-part snub-cube clusters formed by augmentation of a central snub cube’s square faces by six snub cubes of identical chirality to each other, this exhausts the four possibilities. However, multiplying the possibilities would be easy, by adding more components, using other polyhedra, mixing chiralities within the set of polyhedra added during an augmentation, and/or mixing consistent and inconsistent chirality, at different stages of the growth of a polyhedral cluster formed via repeated augmentation.
All the images in this post were created using Stella 4d, which you can try for yourself at this website.
The Greatly Augmented Icosidodecahedron, and Its Dual
If a central polyhedron’s pentagonal and triangular faces are augmented by great dodecahedra and great icosahedra, I refer to it as a “greatly augmented” polyhedron. Here, this has been done with an icosidodecahedron. The same figure appears below, but in “rainbow color” mode.
In the next image, “color by face type,” based on symmetry, was used.
The next image shows the dual of this polyhedral cluster, with face color chosen on the basis of number of sides.

Here is another version of the dual, this one in “rainbow color” mode.
Finally, this image of the dual is colored based on face type.
These six images were made with Stella 4d, which may be found here.
A Rhombicosidodecahedron, Made of Rhombicosidodecahedra
This “metarhombicosidodecahedron” took a long time to build, using Stella 4d, which you can find at http://www.software3d.com/Stella.php — so, when I finished it, I made five different versions of it, by altering the coloring settings. I hope you like it.
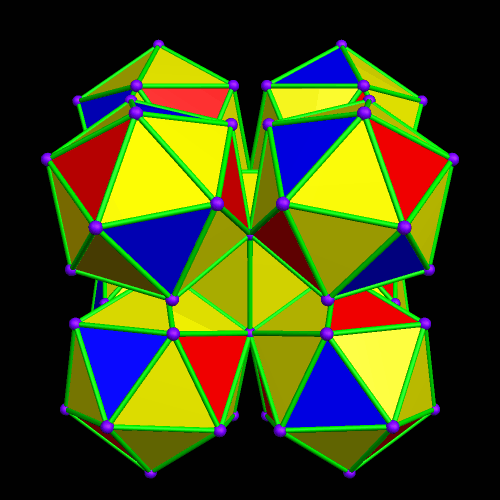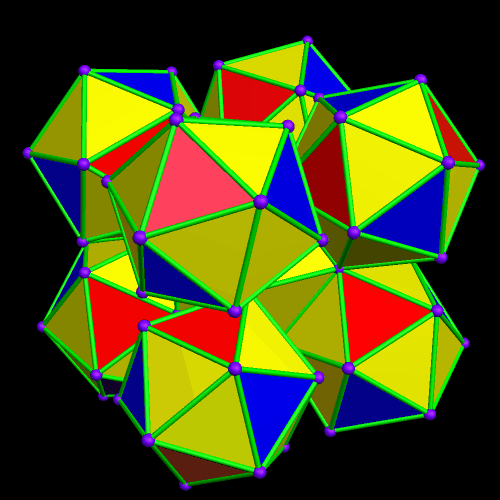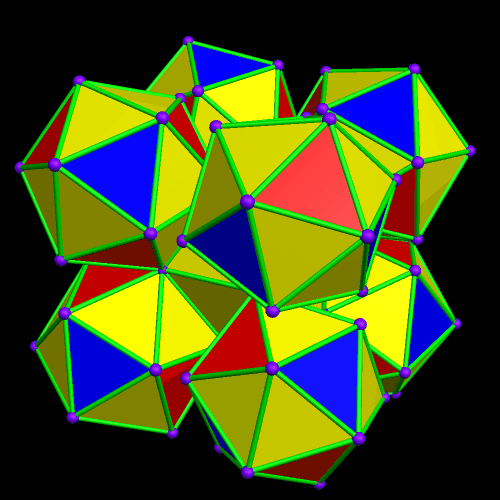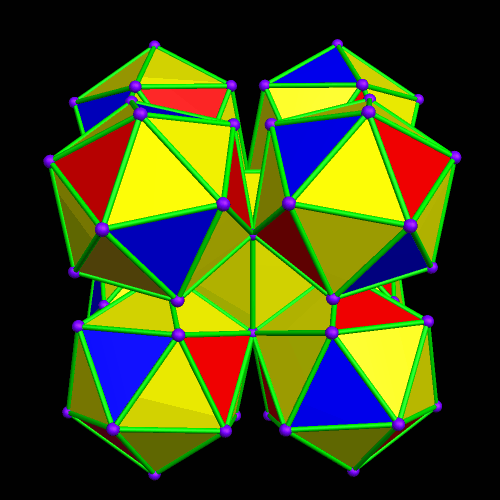
Three Polyhedral Clusters of Icosahedra
In the last post on this blog, there were three images, and the first of these was a rotating icosahedron, rendered in three face-colors. After making it, I decided to see what I could build, using these tri-colored icosahedra as building blocks. Augmenting the central icosahedron’s red and blue faces with identical icosahedra creates this cubic cluster of nine icosahedra:
If, on the other hand, this augmentation is performed only on the blue faces of the central icosahedron, the result is a tetrahedral cluster of five icosahedra:
The next augmentation I performed started with this tetrahedral cluster of five icosahedra, and added twelve more of these icosahedra, one on each of the blue faces of the four outer icosahedra. The result is a cluster of 17 icosahedra, with an overall icosahedral shape.
All of these images were made using Stella 4d, which is available at http://www.software3d.com/Stella.php.