Tag Archives: cube

Two Hourglass Cubes

Image

Reply

Hourglass Cube

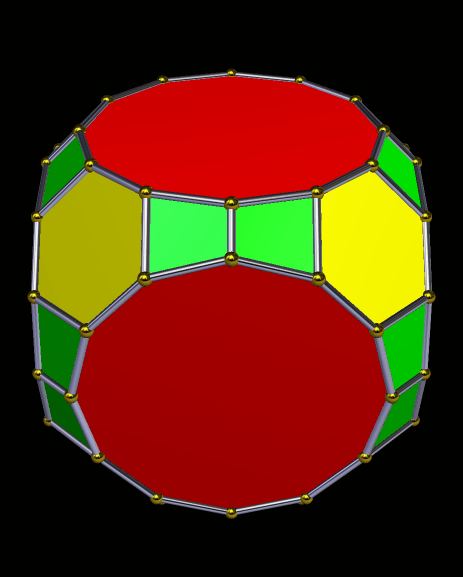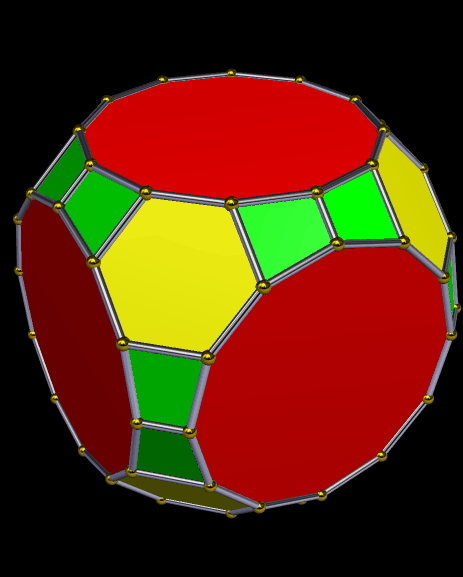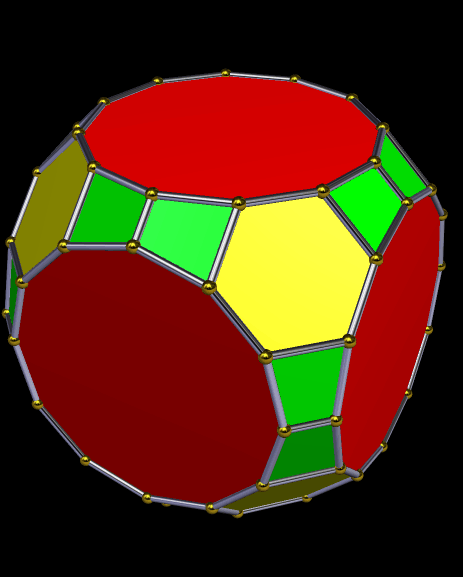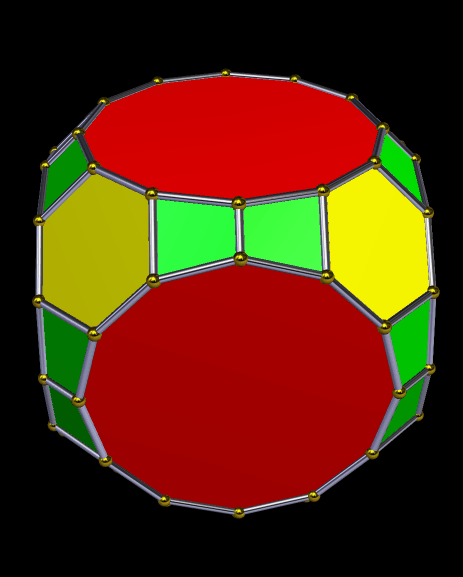
There are two six-member sets of hourglasses in the near-cube above, each of which is made of four not-quite-coplanar faces. One set is green and blue, while the other is magenta and blue.

If the polyhedron above is stellated nine times, the hourglasses expand until they compose the entire polyhedron. (To enlarge it, simply click on it.)

Hourglass cube

Software credit:  all images here were created using Stella 4d. You may try it for yourself as a free trial version, or purchase the fully-functioning version, at http://www.software3d.com/Stella.php.

Cube-Based Polyhedron Featuring Regular Icosagons, Regular Hexagons, and Isosceles Trapezoids

Image

Reply

Polyhedron Featuring Regular Icosagons, Regular Hexagons, and Isosceles Trapezoids

Created with software you can try and/or buy at http://www.software3d.com.Stella.php.

Cube-Based Polyhedron Featuring Regular Icosagons, Equilateral Triangles, Isosceles Trapezoids, and Rectangles

Image

Reply

Polyhedron Featuring Regular Icosagons, Equilateral Triangles, Trapezoids, and Rectangles

Created with software you can try and/or buy at http://www.software3d.com.Stella.php.

A Cube-Based “Bowtie” Symmetrohedron Featuring Six Regular Hexadecagons, Eight Equilateral Triangles, and Two Dozen Each of Two Types of Icosceles Trapezoid

Image

Reply

A Cube-Based Symmetrohedron Featuring Six Regular Hexadecagons, Eight Equilateral Triangles, and Two Types of Icosceles Trapezoids

The two types of trapezoid are shown in blue and green. There are twenty-four blue ones (in eights set of three, surrounding each triangle) and twenty-four green ones (in twelve sets of two, with each set in “bowtie” formation).

This symmetrohedron follows logically from one that was already known, and pictured at http://www.cgl.uwaterloo.ca/~csk/projects/symmetrohedra/, with the name “bowtie cube.” Here’s a rotating version of it.

dodecagons and hexagons

(Images created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)

The Deconstruction of the Compound of Five Cubes

Posted on by
Reply

An Examination of the Compound of Five Cubes

To make the compound of five cubes, begin with a dodecahedron, as seen above. Next, add segments as new edges, and let them be all of the diagonals of all the dodecahedron’s faces. Then, remove the pentagonal faces, as well as the original edges. What’s left is five cubes, in this arrangement.

Cubes 5

Using polyhedral manipulation software called Stella 4d (available at www.software3d.com/Stella.php), these five cubes can be removed one at a time. The first removal has this result:

Cubes 5-1

That left four cubes, so the next removal leaves three:

Cubes 5-2

And then only two:

Cubes 5-3

And, finally, only one remains:

Cubes 5-4

Because their edges were pentagon-diagonals for the original dodecahedron, each of these cubes has an edge length equal to the Golden Ratio, (1 + √5)/2, times the edge length of that dodecahedron.

A Close-Packing of Space, Using Three Different Polyhedra

Image

Reply

A Close-Packing of Space, Using Three Different Polyhedra

This is like a tessellation, but in three dimensions, rather than two. The pattern can be repeated to fill all of space, using cubes (yellow), truncated octahedra (blue), and great rhombcuboctahedra, also known as truncated cuboctahedra (red).

Software credit: see www.software3d.com/stella.php to try or buy Stella 4d, the software I used to create this image.

A Cubic Cluster of Rhombicosidodecahedra

Image

Reply

A Cubic Cluster of Rhombicosidodecahedra

I made this, using Stella 4d, by augmenting each face of an octahedron with a rhombicosidodecahedron. You can give this program a try yourself, for free, at http://www.software3d.com/stella.php.

A Polyhedron Featuring Kites and Regular Dodecagons

Image

1

A Polyhedron Featuring Kites and Regular Dodecagons

The dodecagons are in the same planes as a cube’s faces, so there are six of them. Also, this could be constructed via an unusual truncation of the cube, using three different truncation-planes at each vertex. This polyhedron has thirty faces: the six dodecagons, and twenty-four kites (in eight sets of three).

Software credit: see http://www.software3d.com/stella.php for a free trial download of Stella 4d, the software I used to construct this polyhedron.

A Breathing Cube

Image

Reply

A Breathing Cube

This software used to make this image, Stella 4d, may be tried for free at http://www.software3d.com/stella.php. The “breathing” effect is optional with this program, and is created by having the software use a tight fit-to-frame in each still pic that composes this .gif file.

A Cubic Arrangement of Truncated Octahedra

Image

Reply

A Cubic Arrangement of Truncated Octahedra

This cubic arrangement of eight truncated octahedra has a hole in the center, and indentations in the center of each face of the cube. What would fit in these gaps? More truncated octahedra of the same size, that’s what. This wouldn’t be true for most polyhedra, but the truncated octahedron is unusual in that it can fill space without leaving gaps — much like hexagons can tile a plane, but in three dimensions.

Stella 4d was used to create this image, and you may try it for free at http://www.software3d.com/stella.php.