An Experiment Involving Augmentation of Octahedra with More Octahedra, Etc.

Posted on 11 November 2014 by RobertLovesPi

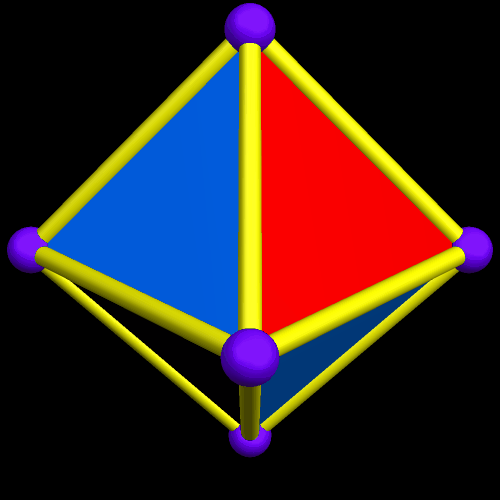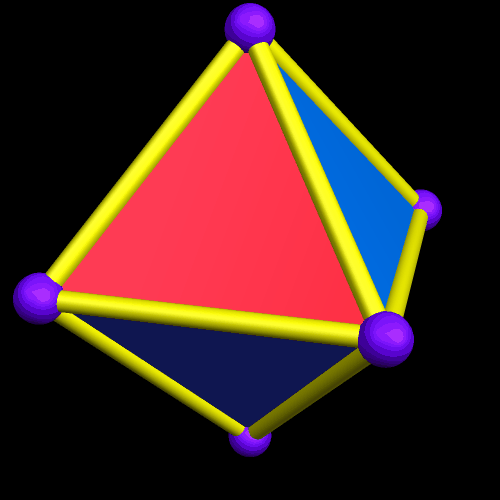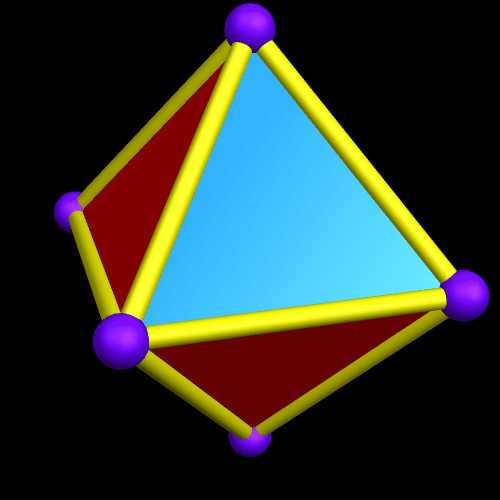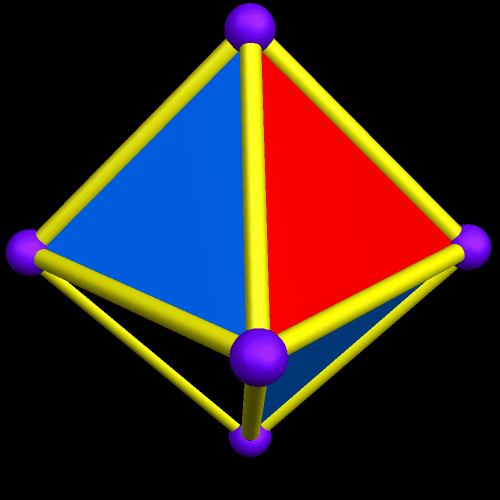
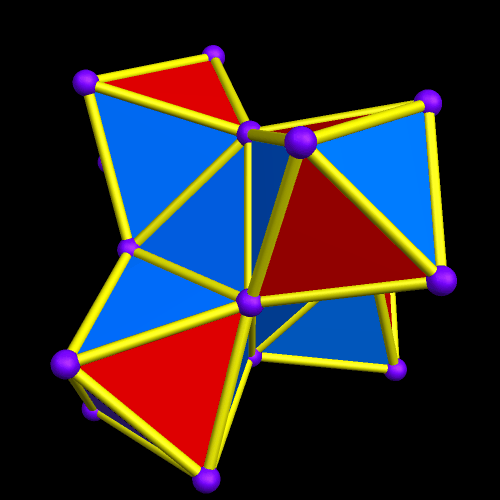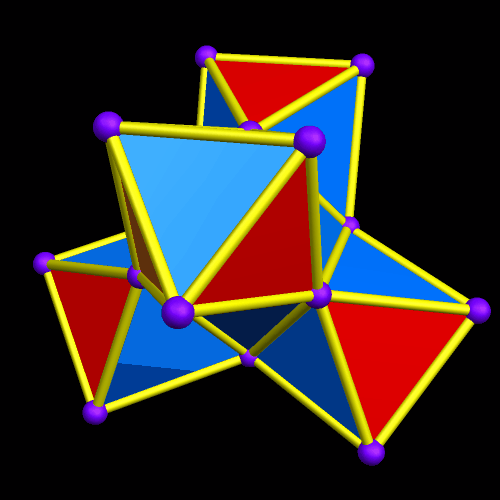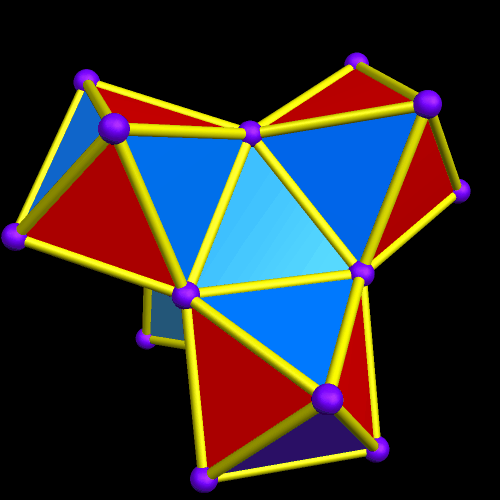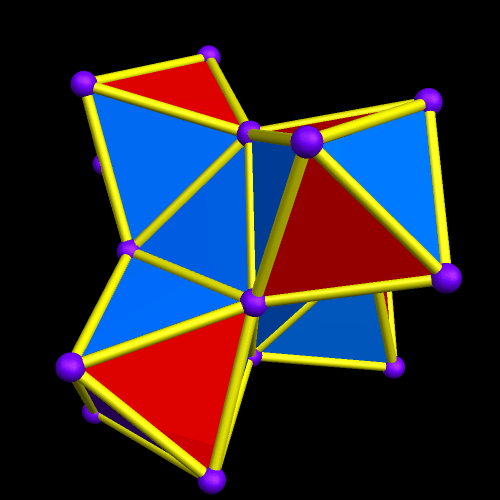
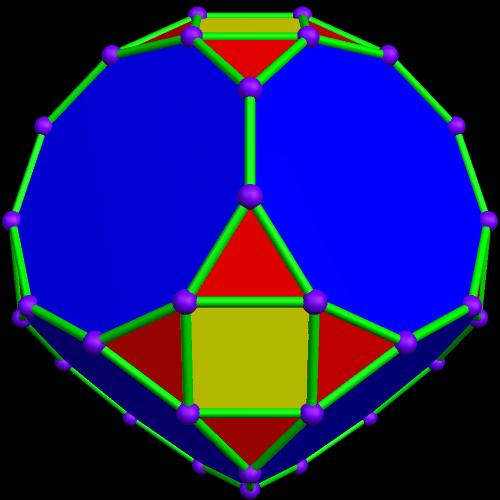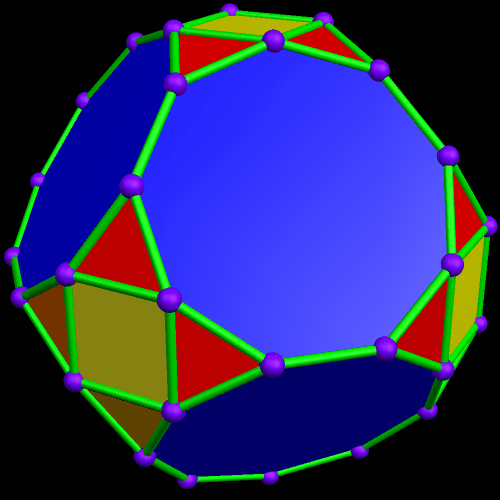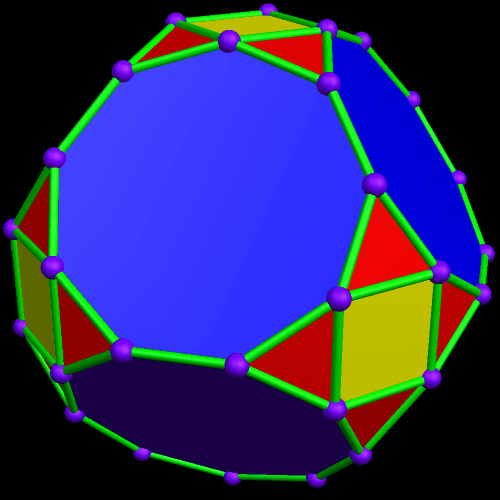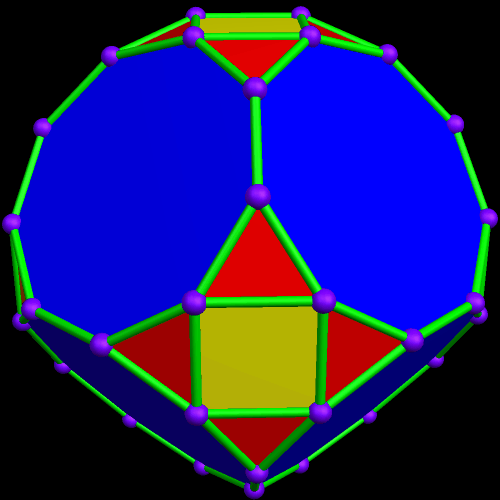
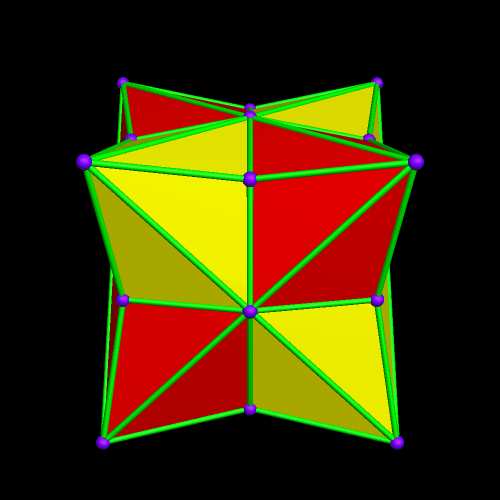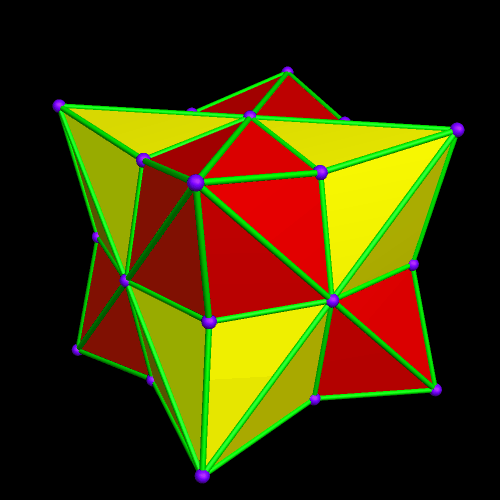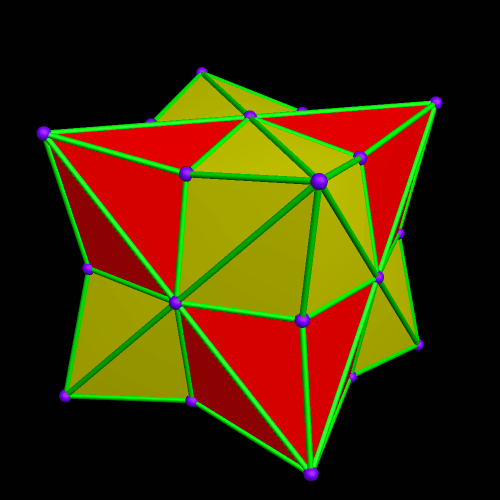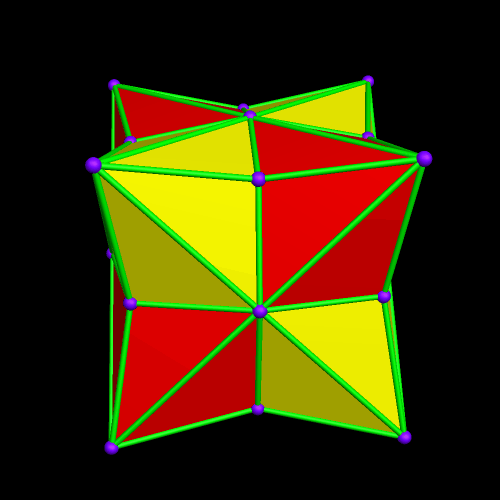
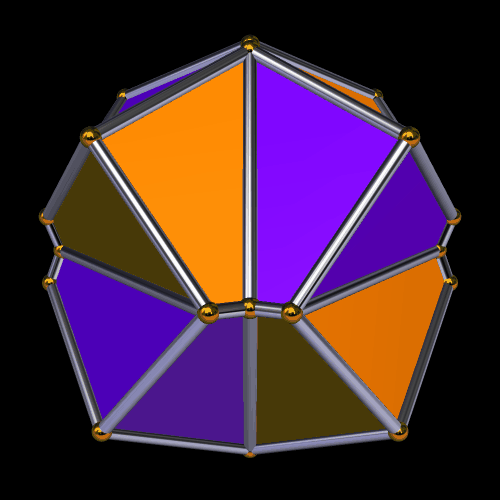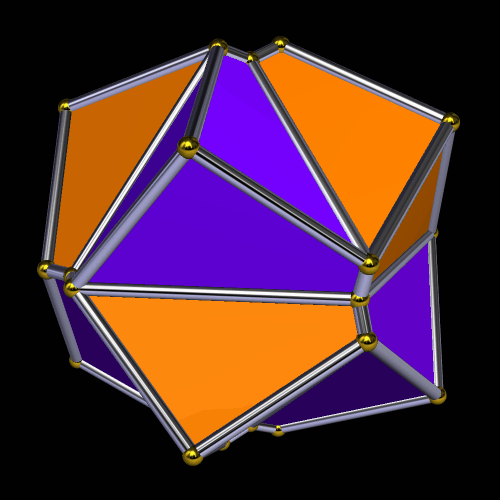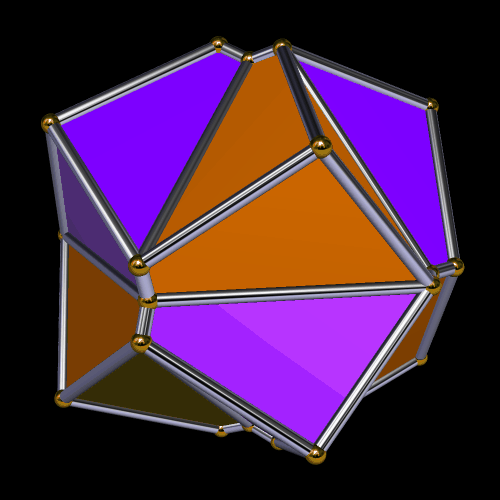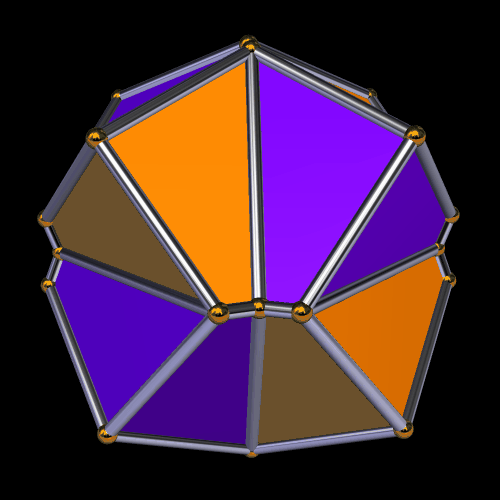
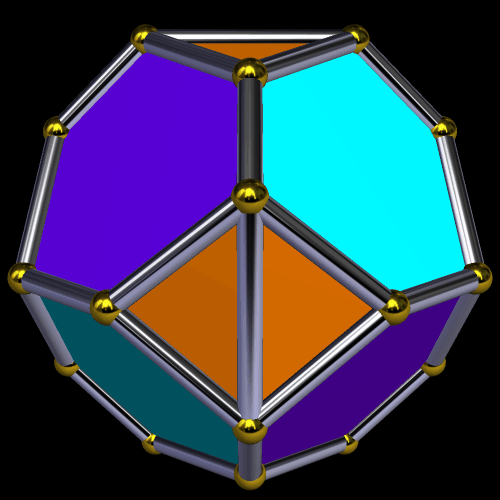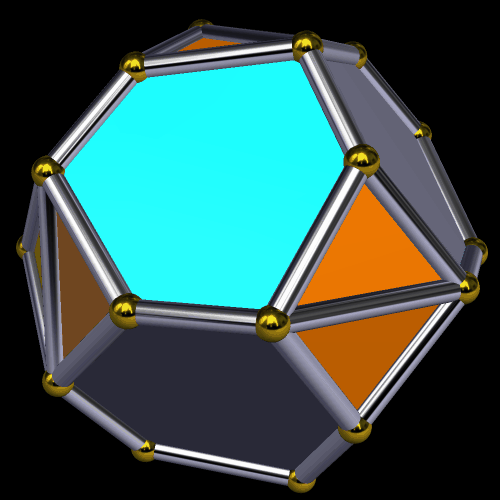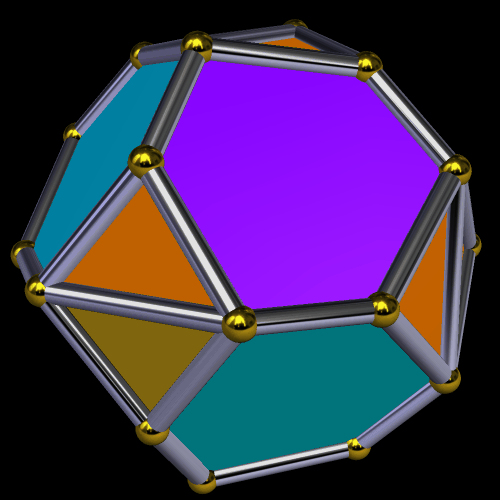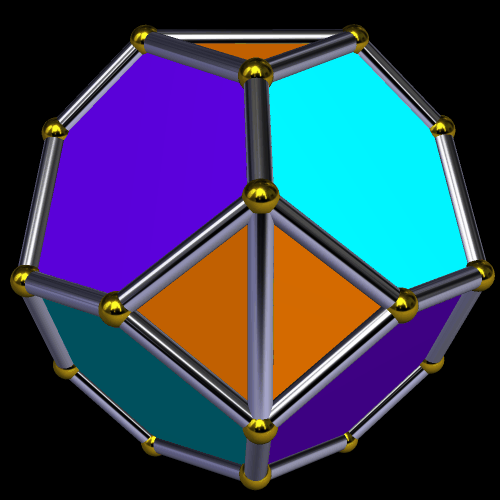
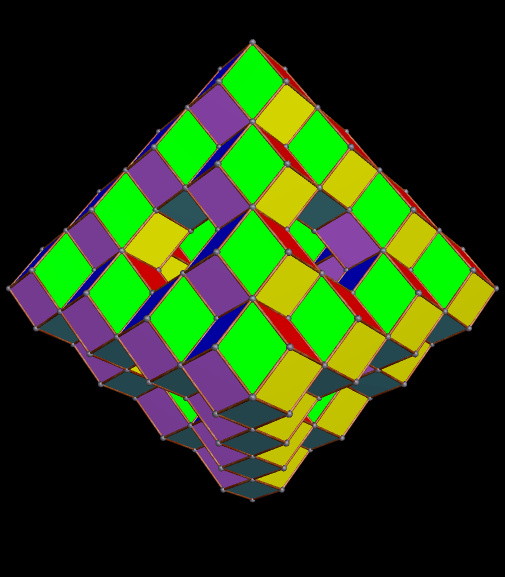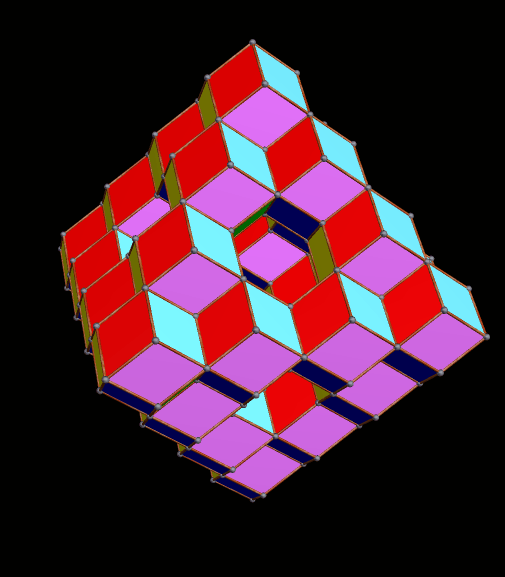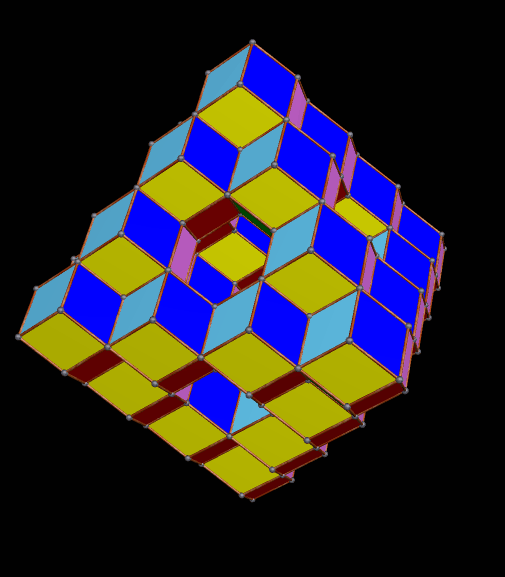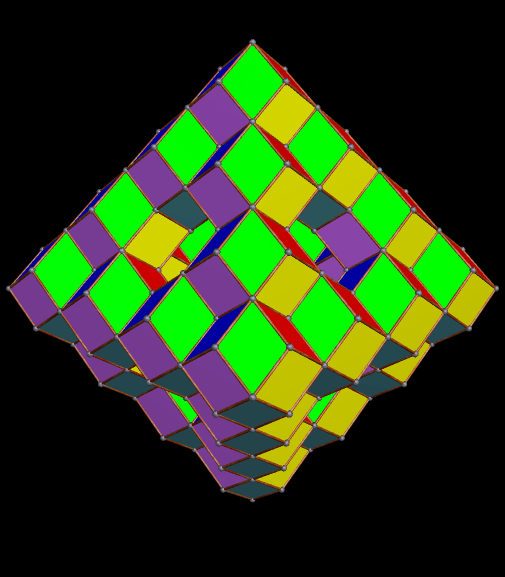
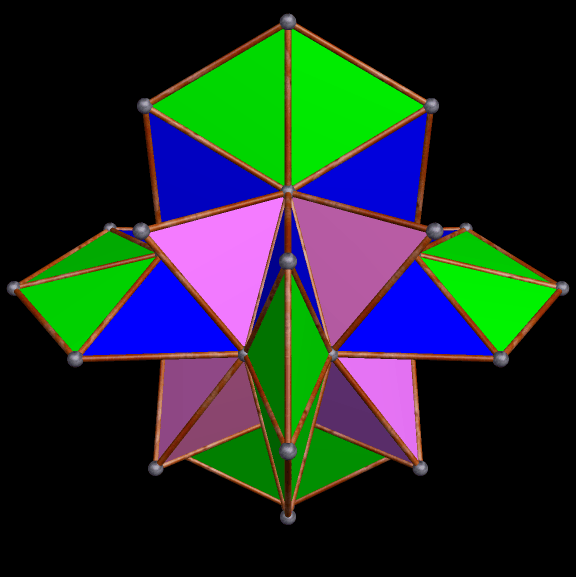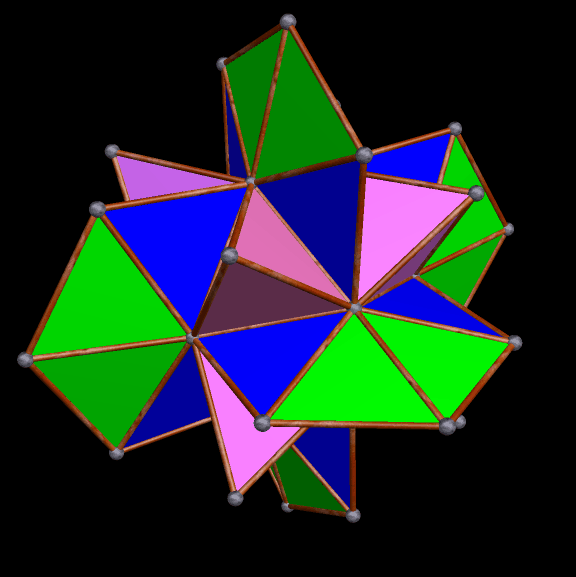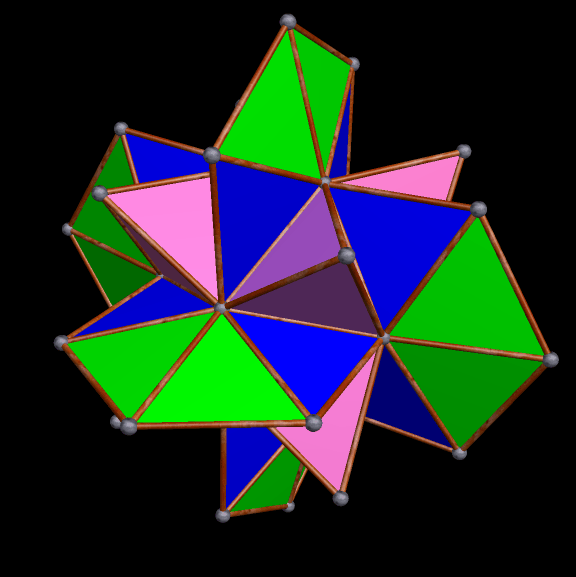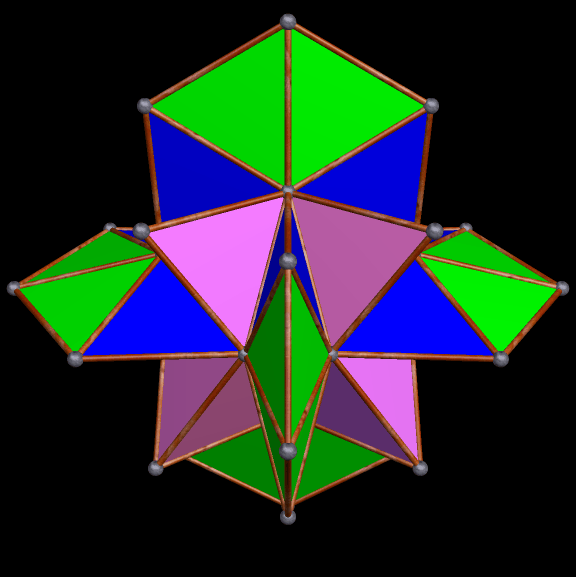
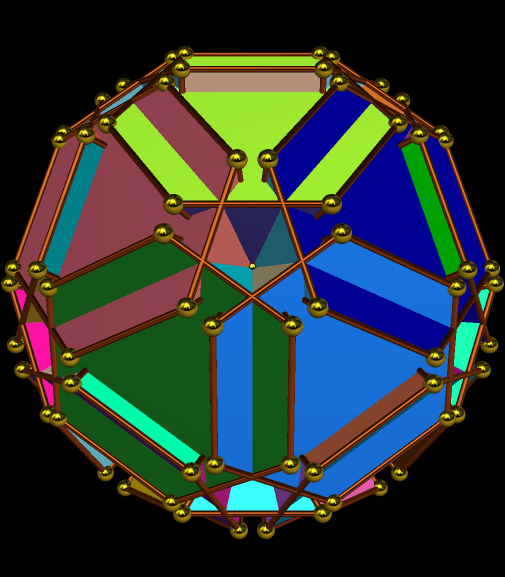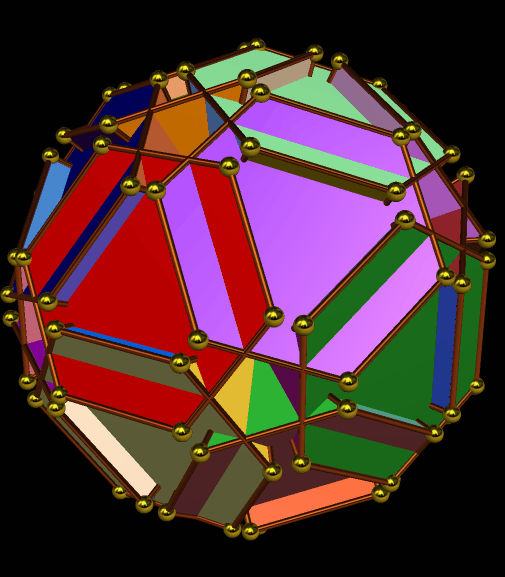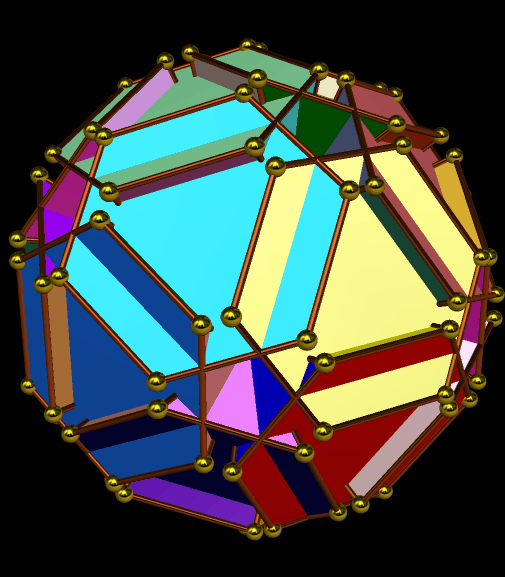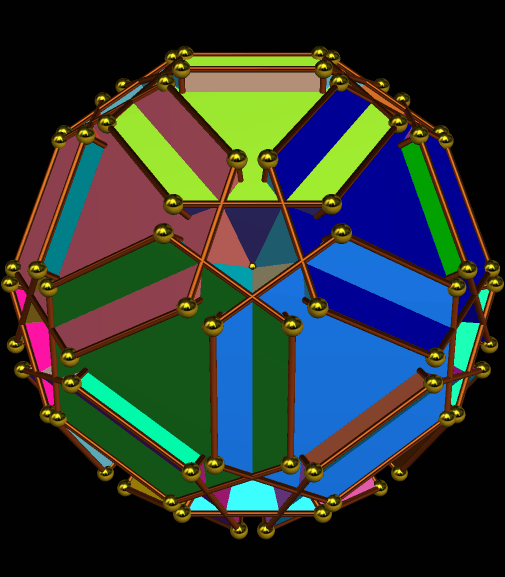
I’m going to start this experiment with a single octahedron, with faces in two colors, placed so that two faces which share an edge are always of different colors.

Next, I will augment the red faces — and only the red faces — with identical octahedra.

The regions with four blue, adjacent faces look as though they might hold icosahedra — but I checked, and they don’t quite fit. I will therefore continue the same process — augmenting only the red faces with more octahedra of the original type.

I’ve now decided that I definitely like this game, so I’ll keep playing it.

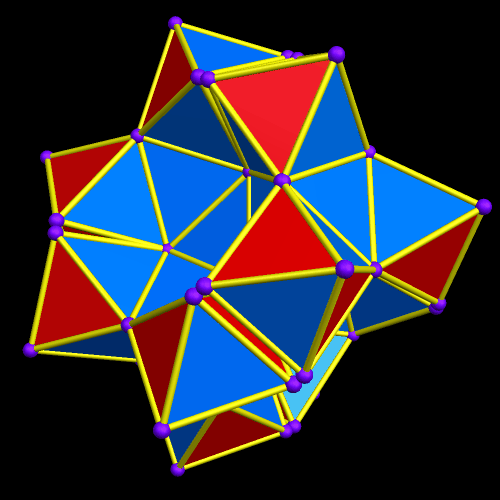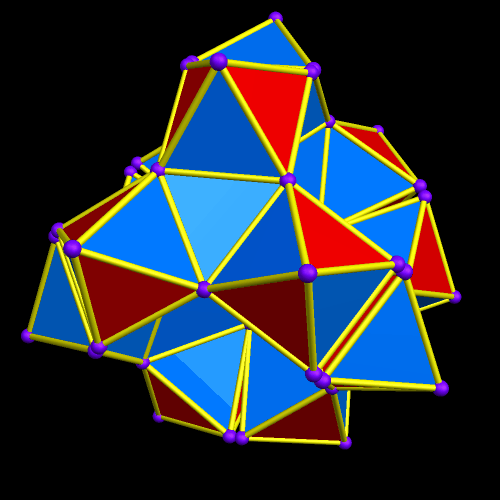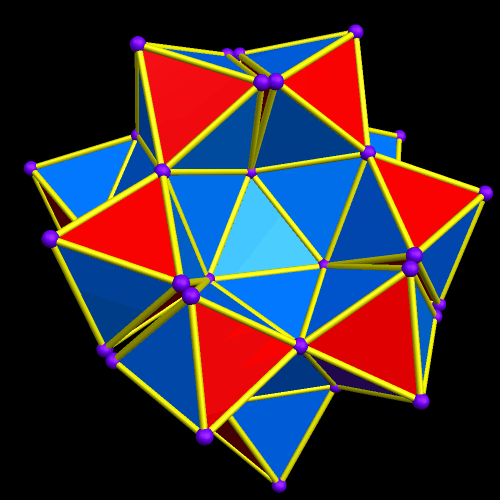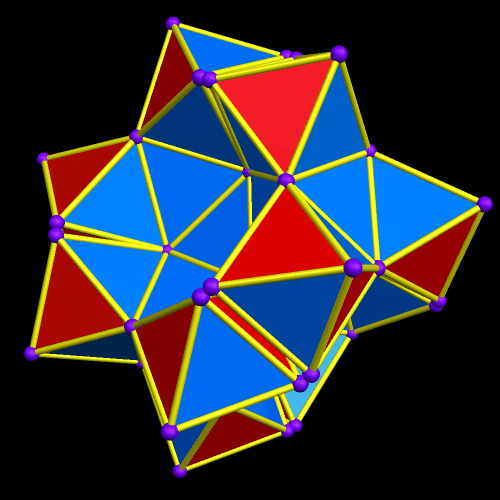
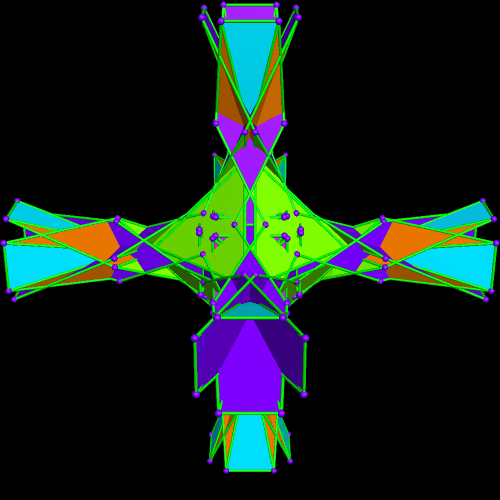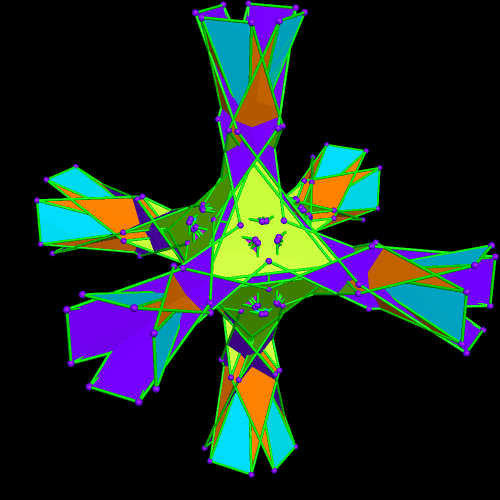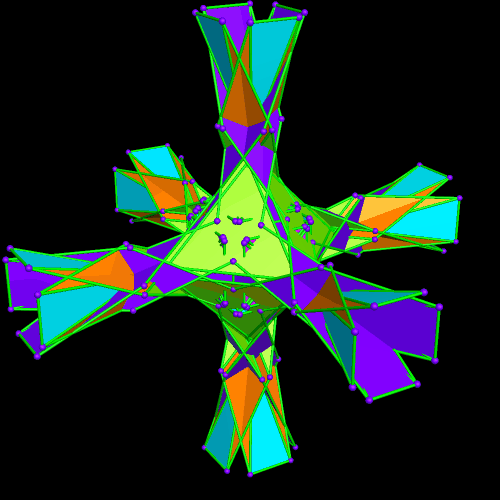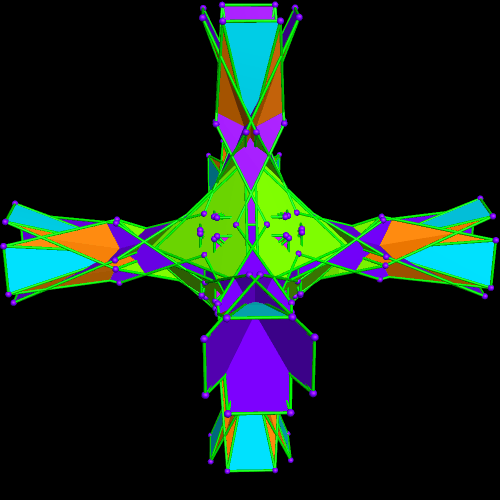
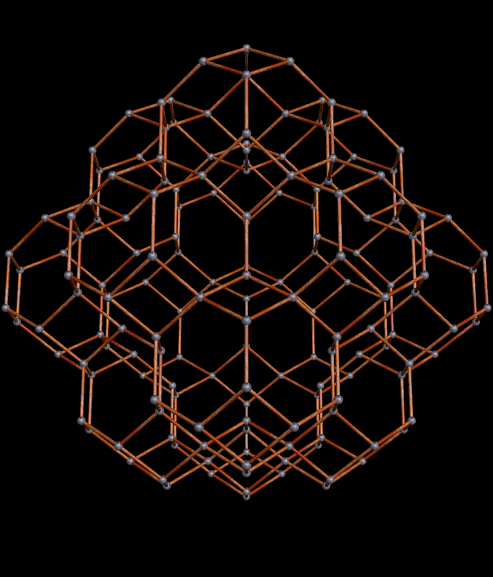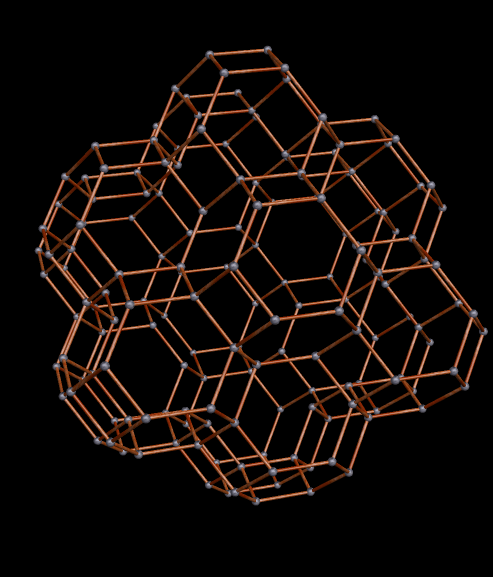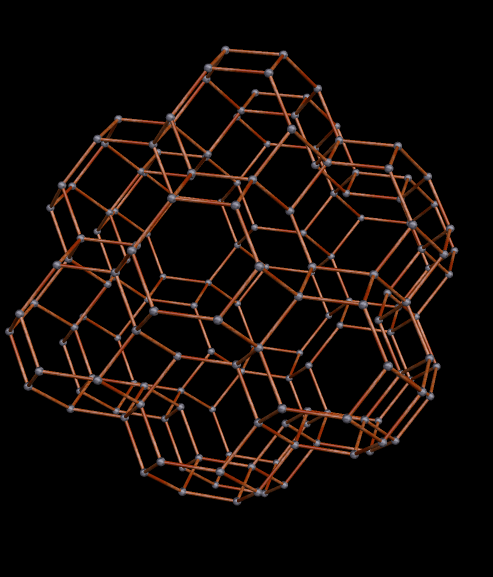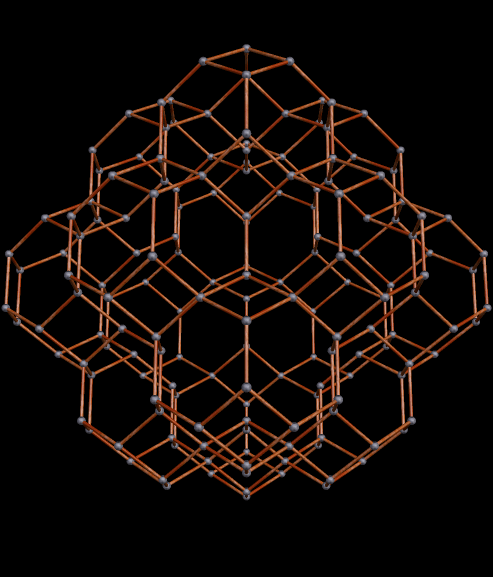
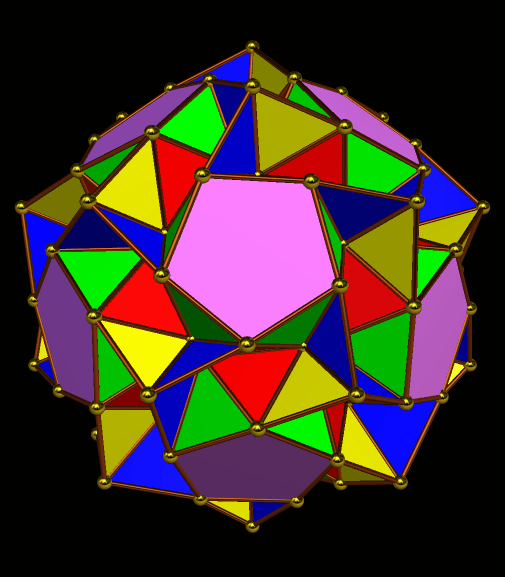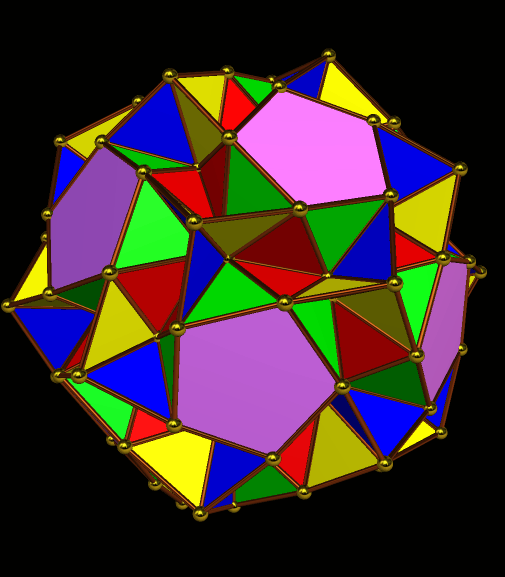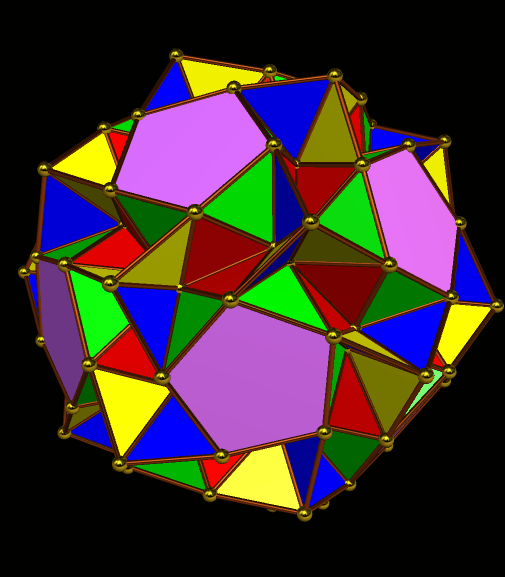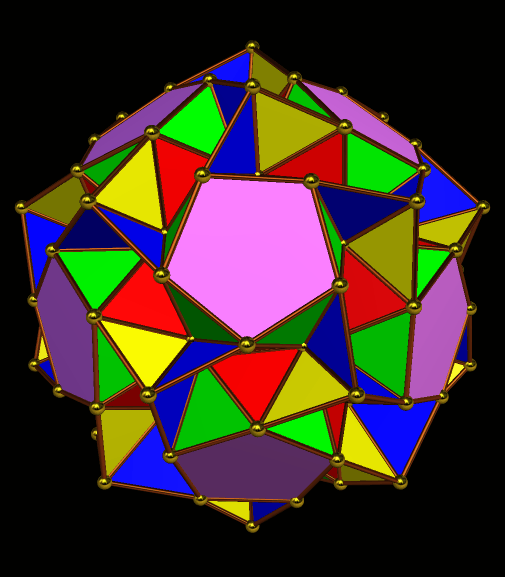
Immediately above, at the fourth of these images, some of the octahedra have started to overlap slightly, but I’m choosing to not be bothered by that — I’m continuing the now-established pattern, just in order to see where it takes me.

The regions of overlap are now far more obvious, but I’m continuing, anyway. Why? Because this is fun, that’s why! Right now, Stella 4d, the program I use to do these polyhedral manipulations, is chugging away on the next one. (This program is avilable at http://www.software3.com/Stella.php.) Ah, it’s ready — here it is!

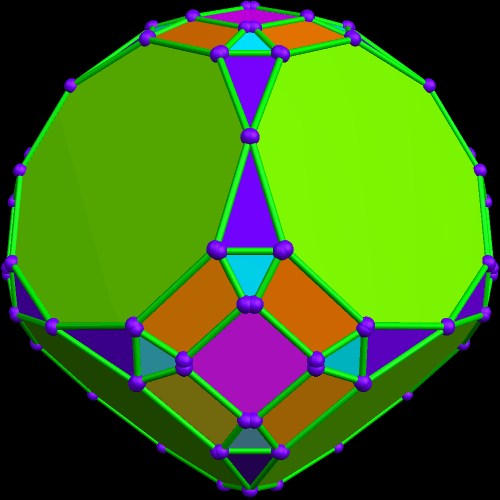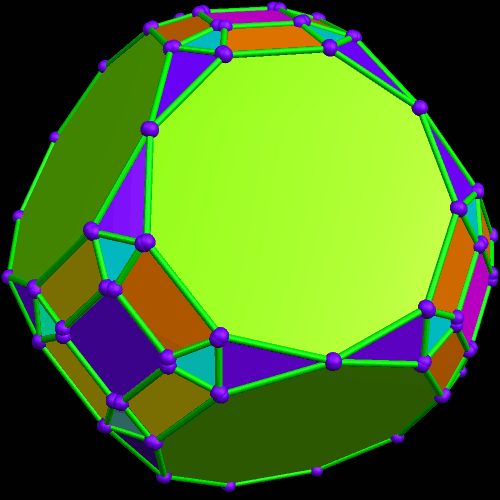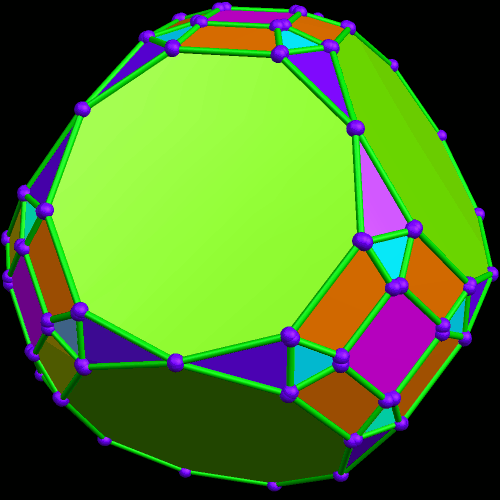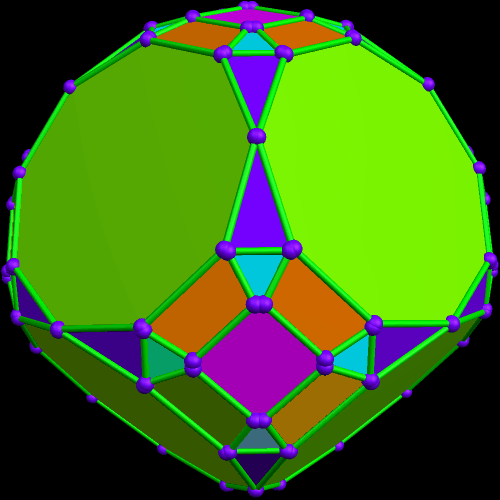
Rather than repeat this process again, I now have another question: what would the convex hull of this figure look like? (A convex hull of a non-convex polyhedron is the smallest convex polyhedron which can contain a given non-convex polyhedron.) With Stella 4d, that’s easily answered.

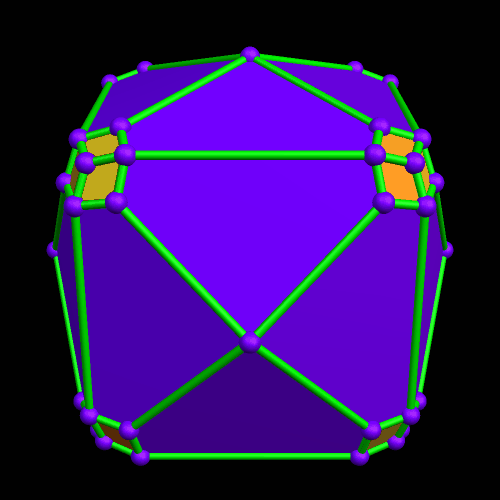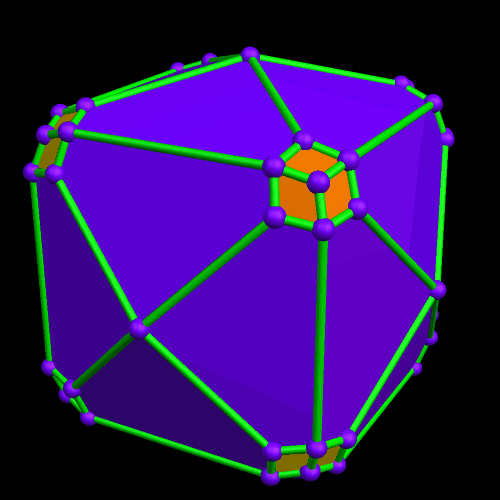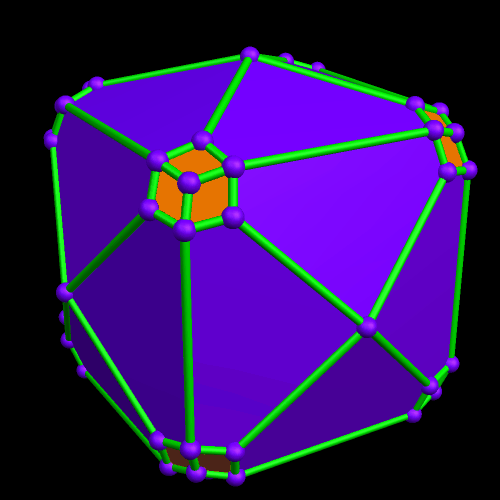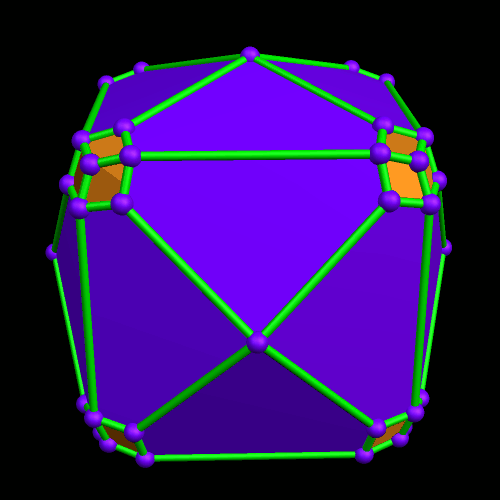
I must admit this: that was nothing like what I expected — but such unexpected discoveries are a large part of what makes these polyhedral investigations with Stella 4d so much fun. And now, to close this particular polyhedral journey, I will have Stella 4d produce, for me, the dual of the convex hull shown above. (In case you aren’t familiar with duality regarding polyhedra, it describes the relationship between the octahedron, with which this post began, and the familar cube. Basically, with duals, faces and verticies are “flipped” over edges, although that is an extremely informal and imprecise way to describe the at the process.)

And with that, my friends, I bid you good night!

A Polyhedral Journey, Beginning with a Near-Miss Johnson Solid Featuring Enneagons

Posted on 9 October 2014 by RobertLovesPi

When Norman Johnson first found, and named, all the Johnson solids in the latter 1960s, he came across a number of “near-misses” — polyhedra which are almost Johnson solids. If you aren’t familiar with the Johnson solids, you can find a definition of them here. The “near-miss” which is most well-known features regular enneagons (nine-sided polygons):

This is the dual of the above polyhedron:

As with all polyhedra and their duals, a compound can be made of these two polyhedra, and here it is:

Finding this polyhedron interesting, I proceeded to use Stella 4d (polyhedron-manipulation software, available at http://www.software3d.com/Stella.php) to make its convex hull.

Here, then, is the dual of this convex hull:

Stella 4d has a “try to make faces regular” function, and I next used it on the polyhedron immediately above. If this function cannot work, though — because making the faces regular is mathematically impossible — one sometimes gets completely unexpected, and interesting, results. Such was the case here.

Next, I found the dual of this latest polyhedron.

The above polyhedron’s “wrinkled” appearance completely surprised me. The next thing I did to change it, once more, was to create this wrinkled polyhedron’s convex hull. A convex hull of a non-convex polyhedron is simply the smallest convex polyhedron which can contain the non-convex polyhedron, and this process often has interesting results.

Next, I created this latest polyhedron’s dual:

I then attempted “try to make faces regular” again, and, once more, had unexpected and interesting results:

The next step was to take the convex hull of this latest polyhedron. In the result, below, all of the faces are kites — two sets of twenty-four each.

I next stellated this kite-faced polyhedron 33 times, looking for an interesting result, and found this:

This looked like a compound to me, so I told Stella 4d to color it as a compound, if possible, and, sure enough, it worked.

The components of this compound looked like triakis tetrahedra to me. The triakis tetrahedron, shown below, is the dual of the truncated tetrahedron. However, I checked the angle measurement of a face, and the components of the above compound-dual are only close, but not quite, to being the same as the true triakis tetrahedron, which is shown below.

This seemed like a logical place to end my latest journey through the world of polyhedra, so I did.

A Zonish Icosahedron, and Some of Its “Relatives”

Posted on 27 September 2014 by RobertLovesPi

To begin this, I used Stella 4d (available here) to create a zonish polyhedron from the icosahedron, by adding zones along the x-, y-, and z-axes. The result has less symmetry than the original, but it is symmetry of a type I find particularly interesting.

After making that figure, I began stellating it, and found a number of interesting polyhedra in this polyhedron’s stellation-series. This is the second such stellation:

This is the 18th stellation:

The next one, the 20th stellation, is simply a distorted version of the Platonic dodecahedron.

This one is the 22nd stellation:

This is the 30th stellation:

The next really interesting stellation I found was the 69th:

At this point, I returned to the original polyhedron at the top of this post, and examined its dual. It has 24 faces, all of which are quadrilaterals.

This is the third stellation of this dual — and another distorted Platonic dodecahedron.

This is the dual’s 7th stellation:

And this one is the dual’s 18th stellation:

At this point, I took the convex hull of this 18th stellation of the original polyhedron’s dual, and here’s what appeared:

Here is this convex hull’s dual:

Stella 4d, the program I use to make these (available here), has a built-in “try to make faces regular” function. When possible, it works quite well, but making the faces of a polyhedron regular, or even close to regular, is not always possible. I tried it on the polyhedron immediately above, and obtained this interesting result:

While interesting, this also struck me as a dead end, so I returned to the red-and-yellow convex hull which is the third image above, from right here, and started stellating it. At the 19th stellation of this convex hull, I found this:

I also found an interesting polyhedron as the 19th stellation of the dual which is three images above:

A Cluster-Polyhedron Formed By 15 Truncated Octahedra, Plus Variations

Posted on 21 September 2014 by RobertLovesPi

To form the cluster-polyhedron above, I started with one truncated octahedron in the center, and then augmented each of its fourteen faces with another truncated octahedron. Since the truncated octahedron is a space-filling polyhedron, this cluster-polyhedron has no gaps, nor overlaps. The same cluster-polyhedron is below, but colored differently: each set of parallel faces gets a color of its own.

This is the cluster-polyhedron’s sixth stellation, using the same coloring-scheme as in the last image:

Here’s the sixth stellation again, but with the coloring scheme that Stella 4d: Polyhedron Navigator (the program I use to make these images) calls “color by face type.” If you’d like to try Stella for yourself, you can do so here.

Also colored by face-type, here are the 12th, 19th, and 86th stellations.

Leaving stellations now, and returning to the original cluster-polyhedron, here is its dual.

This image reveals little about this dual, however, for much of its structure is internal. So that this internal structure may be seen, here is the same polyhedron, but with only its edges visible.

Finally, here is an edge-rendering of the original cluster-polyhedron, but with vertices shown as well — just not the faces.

A Hollow Octahedron Made of Rhombic Dodecahedra, with Variations

Posted on 19 September 2014 by RobertLovesPi

The original polyhedral cluster I built using Stella 4d (available here) is above. Below is its 29th stellation.

And the 30th stellation, as well:

This is the original polyhedral cluster’s dual:

The next image is a variant of the original polyhedral cluster, rendered with only its edges, but not faces or vertices, visible. I wish I could remember exactly how I made this variant, but I simply cannot recall the exact methods I used.

This is the dual of the polyhedron shown immediately above, rendered in the same manner:

This is a compound of the two dual polyhedra right before this sentence.

Two Wrinkled Polyhedra, and One of Their Duals

Posted on 13 September 2014 by RobertLovesPi

I recently stumbled upon some wrinkled polyhedra. Such polyhedra have an unusually high amount of surface area, compared to their volumes, relative to most more-familiar polyhedra. The next one shown, below, is the dual of the first one. shown, above.

The two above were made before I received a request to slow down the spin-rate of the polyhedra I post, most of which, in the past, have had a rotational period of four seconds. This next one has the new, slower spin-rate (with T = 6 seconds) which I am now using:

I hope all of my readers prefer this change, especially since it takes 50% more memory, per file, to slow these down to 2/3 their previous rotational speed.

These were all made using Stella 4d, software which can be tried or bought here: http://www.software3d.com/Stella.php.

A Great Dodecahedron, Augmented with Twelve Icosidodecahedra, and Its Dual

Posted on 11 September 2014 by RobertLovesPi

Each face of a great dodecahedron is a regular pentagon, and each of those pentagonal faces has an icosidodecahedron attached to it, in the figure above. The dual of this figure appears below.

Both images were created with Stella 4d, software available at www.software3d.com/Stella.php.

Two Polyhedral Compounds

Posted on 17 August 2014 by RobertLovesPi

The image above is a compound of the rhombic triacontahedron (the dual of the icosidodecahedron) and a strombic hexacontahedron (the dual of the rhombicosidodecahedron). Below, you’ll find a compound of six square-based pyramids, all with their “centers of mass” (assuming uniform density) displaced, from the compound’s center, by equal amounts. In response to a request I have received, polyhedral images which rotate more slowly are coming soon . . . after I have finished posting my backlog of already-produced polyhedral .gif files, since there is no way to slow them down after they are already created.

The program I use for these polyhedral investigations is Stella 4d, available at www.software3d.com/Stella.php.

An Icosahedron, Augmented with Twenty Triangular Cupolae, Together with Its Dual

Posted on 16 August 2014 by RobertLovesPi

After making the above polyhedron using Stella 4d (a program you can try for free at www.software3d.com/Stella.php), I checked its dual, which is shown below. I was surprised at its appearance, for it resembles a stellated polyhedron, even though it was created by a completely different process.