
These enneagrams are of the {9/3} variety, which means each one is made of three concentric, equilateral triangles. One of these enneagrams is at the center; the other nine surround it.

These enneagrams are of the {9/3} variety, which means each one is made of three concentric, equilateral triangles. One of these enneagrams is at the center; the other nine surround it.


This is similar to the polyhedron seen here: https://robertlovespi.wordpress.com/2014/05/21/polyhedron-featuring-twenty-regular-nonagons-twelve-regular-pentagons-and-sixty-isosceles-triangles/. The difference is that the enneagons (also called nonagons) are closer to this polyhedron’s center, causing them to overlap slightly.
Software credit: visit http://www.software3d.com/Stella.php for a free trial download of Stella 4d, the program I used to create this image.

These polygons are known to virtually all speakers of English as the triangle and the quadrilateral, but that doesn’t mean I have to like that fact, and, the truth is, I don’t. Why? There are a couple of reasons, all involving lack of consistency with the established names of other polygons.
Consider the names of the next few polygons, as the number of sides increases: the pentagon, hexagon, heptagon, and octagon. The “-gon” suffix refers to the corners, or angles, of these figures, and is derived from Greek, The end of the word “triangle” also refers to the same thing — but not in Greek. For the sake of consistency, triangles should, instead, be called “trigons.”
In the case of the quadrilateral, the problem is twofold. The suffix “-lateral” refers to sides, not angles. For the sake of consistency, “-gon” should be used instead. The prefix “quadri-” does mean four, of course, but is derived from Latin, not Greek. We use the Greek prefix “tetra-” to refer to four when naming polyhedra (“tetrahedron”), so why not use it for polygons with four sides, also? The best name available for four-sided polygons requires a change in both the prefix and suffix of the word, resulting in the name “tetragon” for the figure on the right.
When I listed the names of higher polygons above, I deliberately stopped with the octagon. Here’s the next polygon, with nine sides and angles:
I’m guilty of inconsistency with the name of nine-sided polygons, myself. All over this blog, you can find references to “nonagons,” and the prefix “nona-” is derived from Latin. Those who already know better have, for years, been calling nine-sided polygons “enneagons,” using the Greek prefix for nine, rather than the Latin prefix, for reasons of consistency. I’m not going to go to the trouble to go back and edit every previous post on this blog to change “nonagon” to “enneagon,” at least right now, but, in future posts, I will join those who use “enneagon.”
Here’s one more, with eleven sides:
I don’t remember ever blogging about polygons with eleven sides, but I have told geometry students, in the past, that they are called “undecagons.” I won’t make that mistake again, for the derivation of that word, as is the case with “nonagon,” uses both Latin and Greek. A better name for the same figure, already in use, is “hendecagon,” and I’m joining the ranks of those who use that term, derived purely from Greek, effective immediately.
With “hendecagon” and “enneagon,” I don’t think use of these better names will cause confusion, given that they are already used with considerable frequency. Unfortunately, that’s not the case with the little-used, relatively-unknown words “trigon” and “tetragon,” so I’ll still be using those more-familiar names I don’t like, just to avoid being asked “What’s a trigon?” or “What’s a tetragon?” repeatedly, for three- and four-sided polygons. Sometimes, I must concede, it is necessary to choose the lesser of two irritations. With “triangle” and “quadrilateral,” this is one of those times.
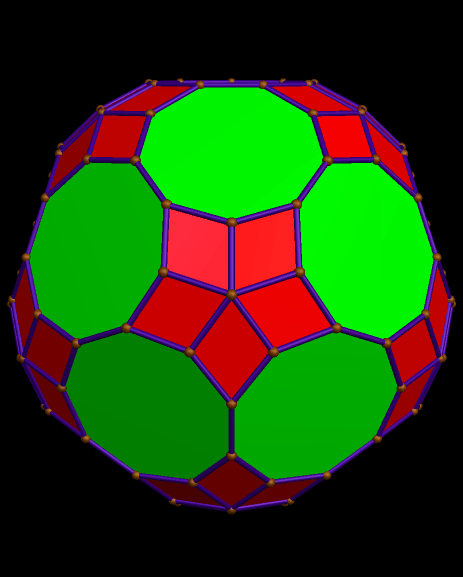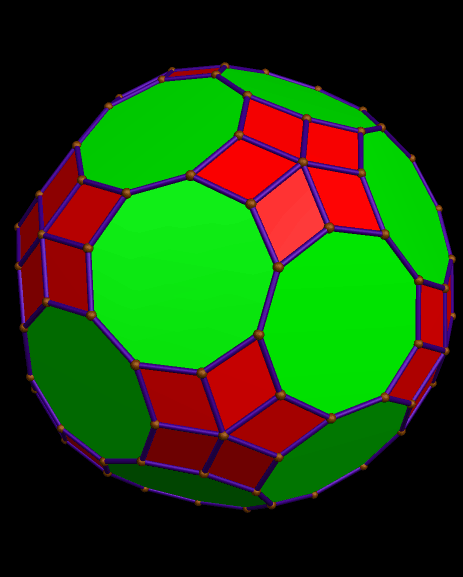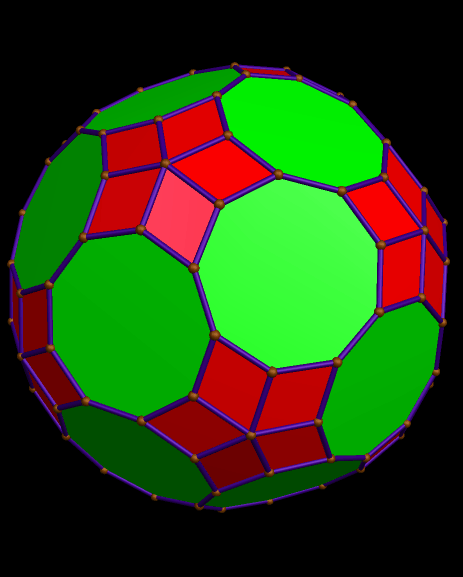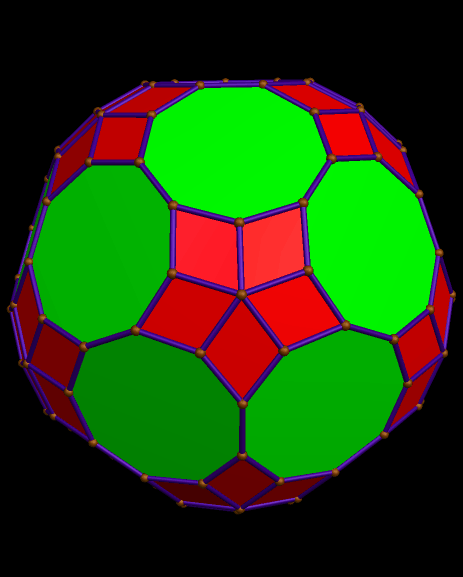
Here is the dual of the solid above, also.
These images were created with Stella 4d, which you can find at http://www.software3d.com/Stella.php.

If the isosceles triangles in this polyhedron were close enough to being equilateral that close inspection would be required to tell the difference, this would be a near-miss to the Johnson Solids. However, in my opinion, this doesn’t meet that test — so I’m calling this a “near-near-miss,” instead.
Software credit: visit this website if you would like to try a free trial download of Stella 4d, the program I used to create this image.

Software credit: just visit http://www.software3d.com/Stella.php to try or buy the software, Stella 4d, which I used to make this polyhedron.


So far as I know, no one knows how many otherwise-regular convex “bowtie” polyhedra exist — that is, convex polyhedra whose only faces are regular polygons, and pairs of isosceles trapezoids in “bowtie” formation. With the aid of software called Stella 4d, which you can find at http://www.software3d.com/Stella.php, I do believe I’ve found another one which hasn’t been seen before.
To make it, I started with what is probably the most well-known near-miss to the Johnson Solids, this polyhedron featuring enneagons (nine-sided polygons; also called “nonagons”):
I then augmented each enneagonal face with regular antiprisms, took the convex hull of the result, and then used Stella’s “try to make faces regular” function — and it worked, making the octagons regular, as well as the enneagons.
Update: It turns out that this polyhedron has been seen before. It’s at http://www.cgl.uwaterloo.ca/~csk/projects/symmetrohedra/ — and there are even more at http://www.cgl.uwaterloo.ca/~csk/papers/kaplan_hart_bridges2001.pdf. These include several more “bowtie” polyhedra found among what those researchers, Craig S. Kaplan and George W. Hart, call “symmetrohedra.” They call this particular polyhedron a “bowtie octahedron.”