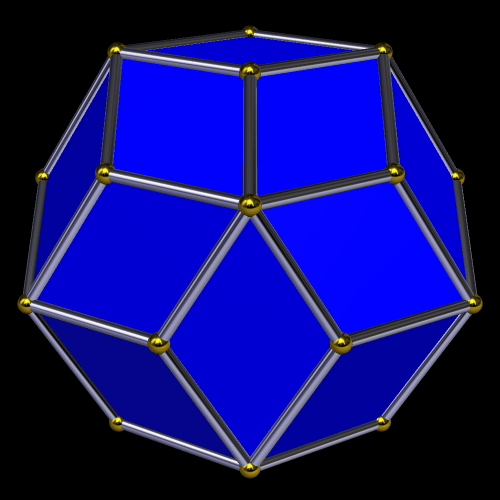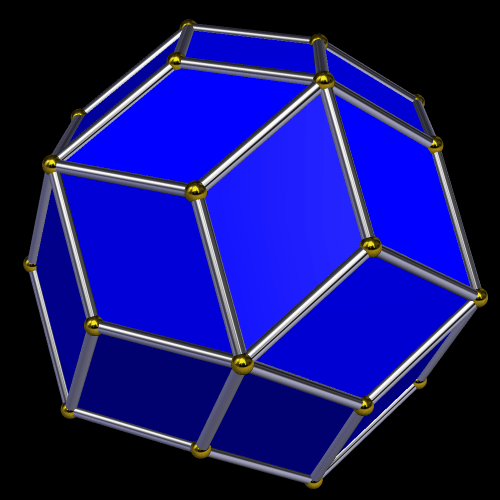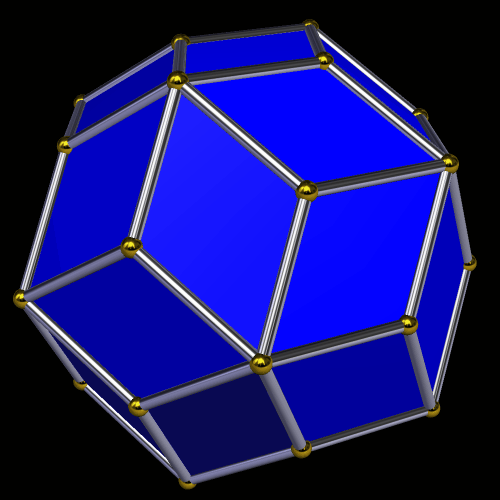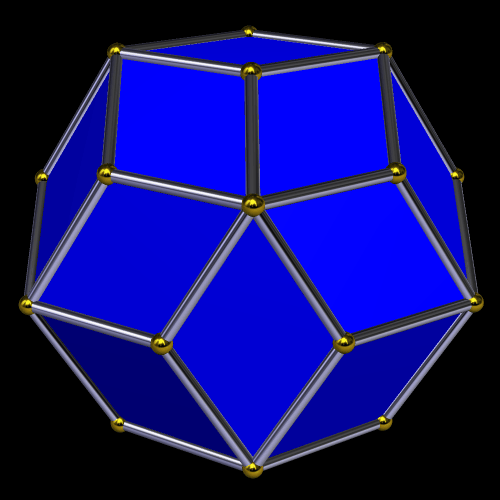
Clusters of Rhombic Triacontahedra

Posted on 2 October 2023 by RobertLovesPi

Here’s a rhombic triacontahedron, possibly the most well-known of the Catalan solids. It’s thirty faces are all golden rhombi (rhombi with their diagonals in the golden ratio).

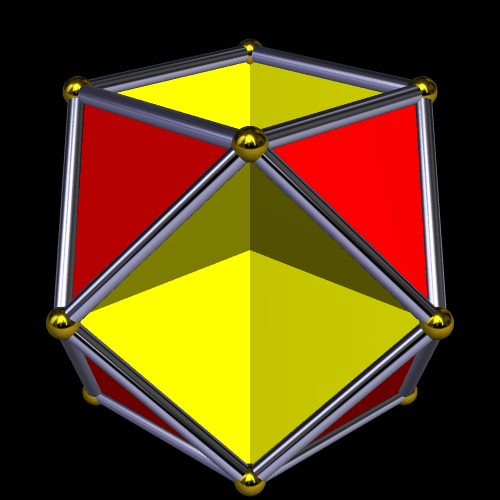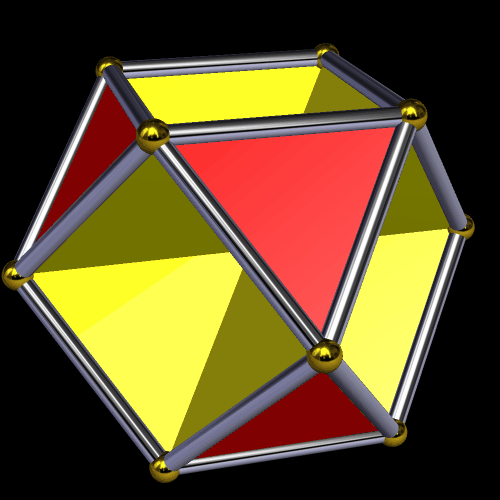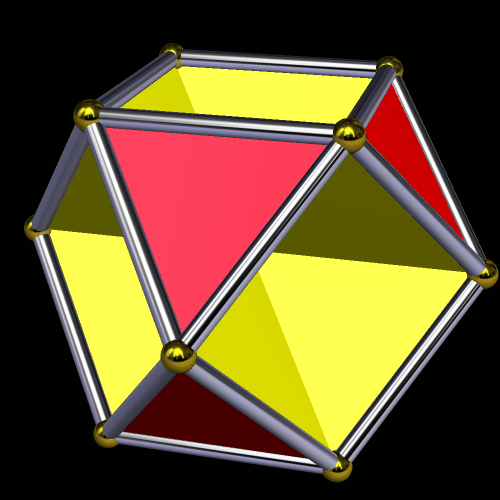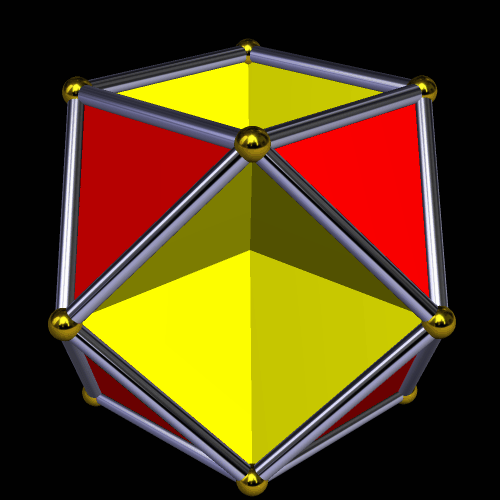
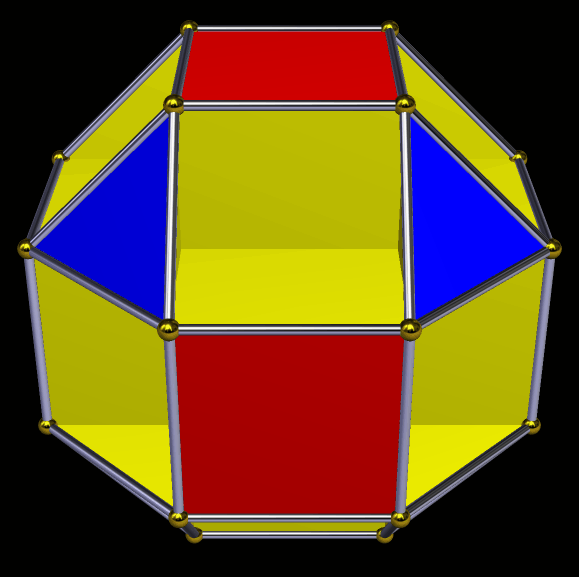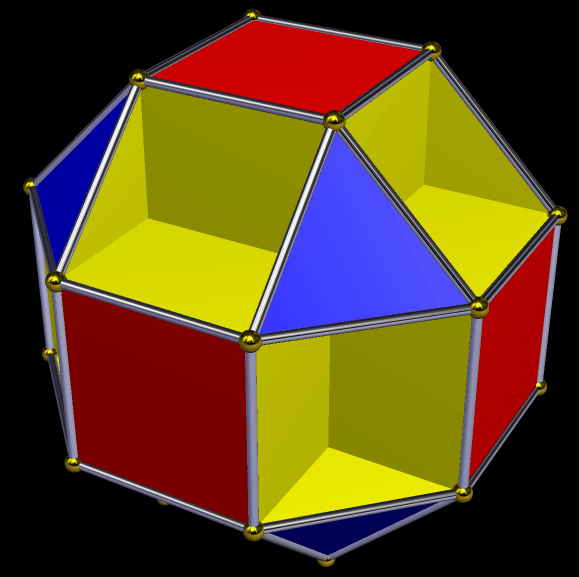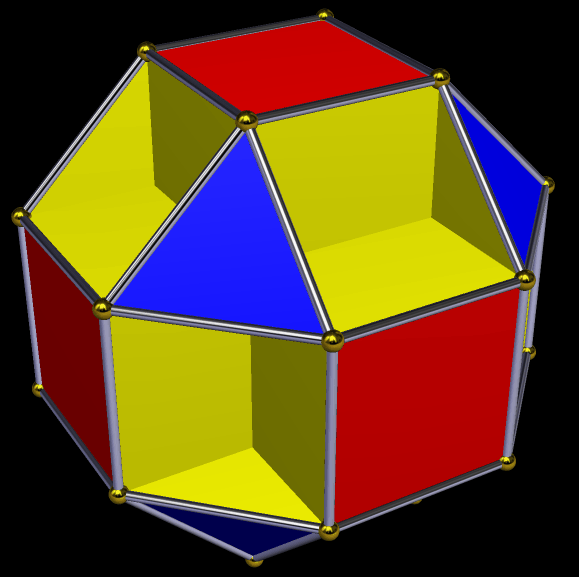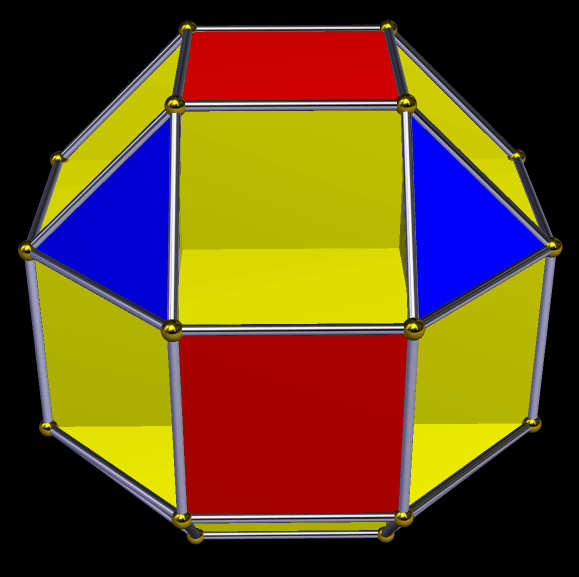
Here’s what you get if you augment each face with another rhombic triacontahedron:

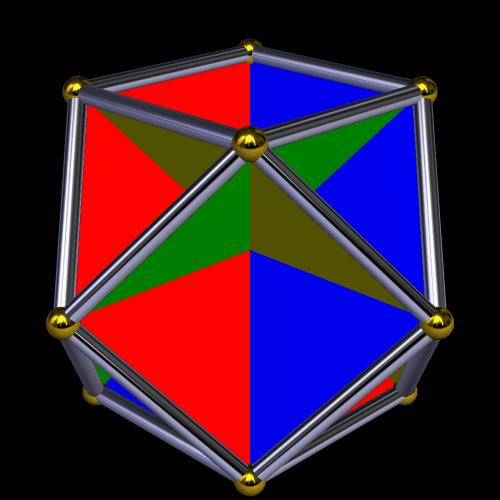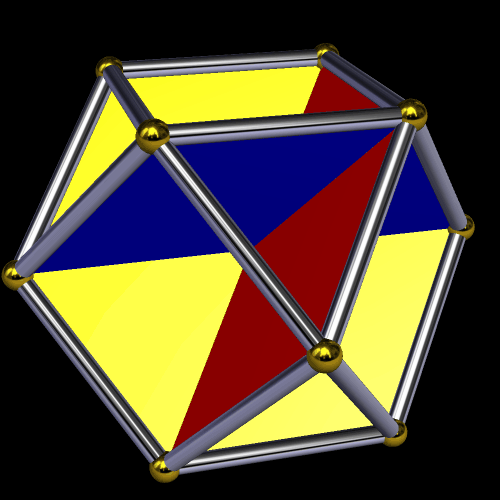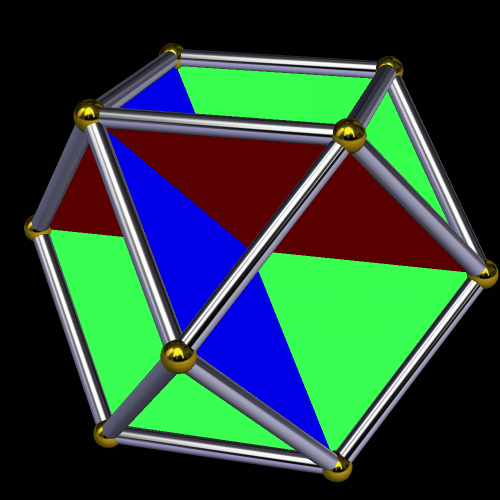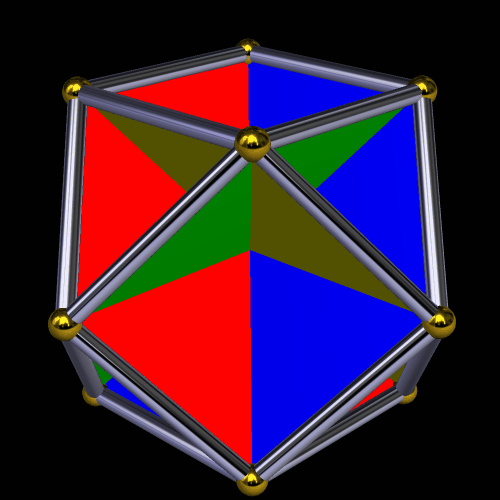
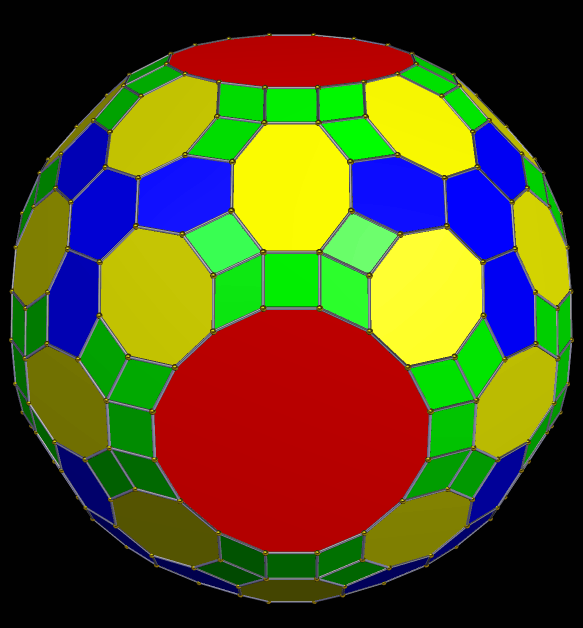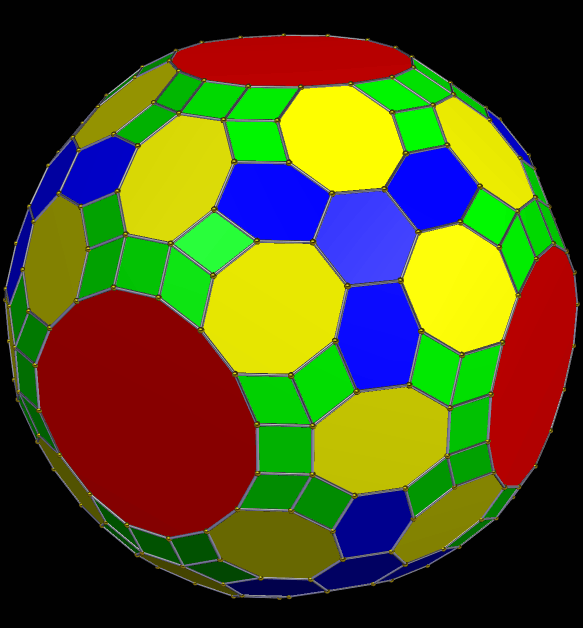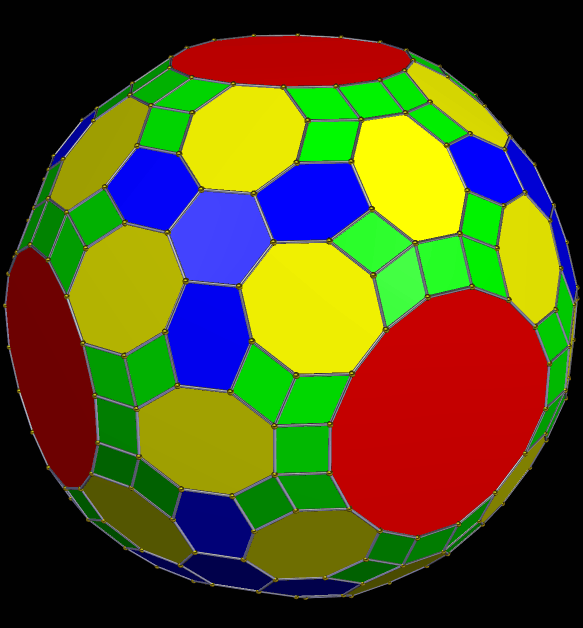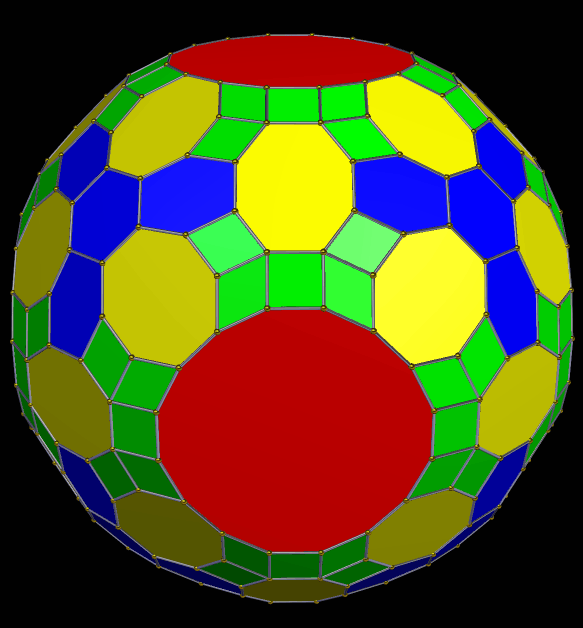
Coloring this cluster-polyhedron by face type has this result:

So what happens if each face of this cluster-polyhedron is augmented by another rhombic triacontahedron? This does:

Here’s another view of that, in “rainbow color mode”:

I made these virtual models with Stella 4d: Polyhedron Navigator. If you’d like to try this software for free, the website to visit is http://www.software3d.com/Stella.php.

Four Interpenetrating Regular Hexagons

Posted on 22 September 2023 by RobertLovesPi

To make the image above, using Stella 4d (available here), I started with a uniform polyhedron called the octahemioctahedron, and then made the triangular faces of it invisible. Here’s what this polyhedron looks like without its triangles hidden:

The convex hull of either of these figures is a cuboctahedron, which is shown below.

Six Interpenetrating Regular Decagons

Posted on 21 September 2023 by RobertLovesPi

To make the image above, using Stella 4d (available here), I started with a uniform polyhedron called the small icosihemidodecahedron, and then made the triangular faces of it invisible. Here’s what this polyhedron looks like without its triangles hidden:

The convex hull of either of these figures is an icosidodecahedron, which is shown below.

A Zonohedron Derived From the Truncated Octahedron

Posted on 20 September 2023 by RobertLovesPi

This zonohedron is made from the truncated octahedron’s vertices, edges, and faces. I made it using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Cluster of Fifteen Cuboctahedra

Posted on 14 September 2023 by RobertLovesPi

There’s one cuboctahedron in the center of this cluster, with each of its fourteen faces augmented by another cuboctahedron. The image below uses coloring of each face by its number of sides, while the next one is in “rainbow color mode.”

I made these images using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Compound of a Strombic Icositetrahedron and the Rhombic Dodecahedron

Posted on 13 September 2023 by RobertLovesPi

I made this using Stella 4d, which you can try for yourself, free, at this website: http://www.software3d.com/Stella.php.

A Truncated Cube, Decorated With Tessellations

Posted on 5 September 2023 by RobertLovesPi

Using Stella 4d (available here), I put this tessellation on the octagonal faces of a truncated octahedron, while hiding the triangular faces. The tessellation itself was made using Geometer’s Sketchpad.

The Great Cubicuboctahedron, and Some of Its Stellations

Posted on 31 August 2023 by RobertLovesPi

The last post here featured the small cubicuboctahedron (one of the uniform solids, a group of polyhedra I’m still learning), so naturally, next, I went looking for the great cubicuboctahedron. Here it is:

This polyhedron comes with a long and interesting stellation-series. I plucked out the ones I liked best, and they are shown below.

I made these virtual models using Stella 4d, which you can try for free at http://www.software3d.com/Stella.php.

A Cube in a Castle

Posted on 30 August 2023 by RobertLovesPi

I made this, using Stella 4d, by repeatedly stellating the small cubicuboctahedron, which is one of the uniform polyhedra. I think it looks like a red cube, sitting securely in the middle of a castle. Here’s what it looks like before these stellations:

If you’d like to try Stella for yourself, the site to visit for a free trial download is http://www.software3d.com/Stella.php.

An All-Kite Modification of the Rhombicosidodecahedron

Posted on 26 August 2023 by RobertLovesPi

To make this polyhedron, I used Stella 4d‘s “morph duals by augmentation” function on a rhombicosidodecahedron. The result has sixty each of two types of kites, for a total of 120 faces.