Selections from the Second Hundred Stellations of the Rhombicosidodecahedron

Posted on 31 May 2015 by RobertLovesPi

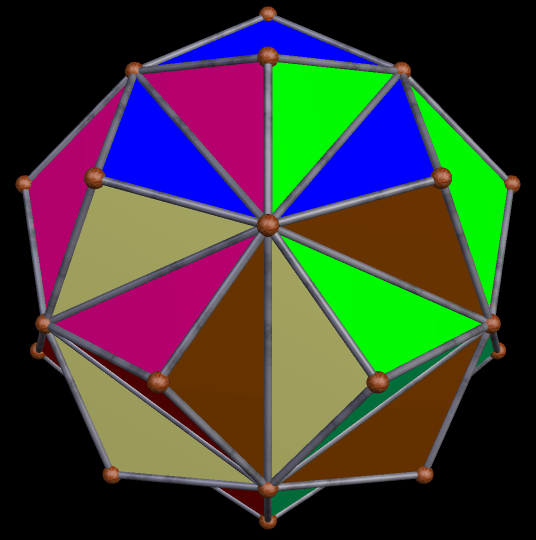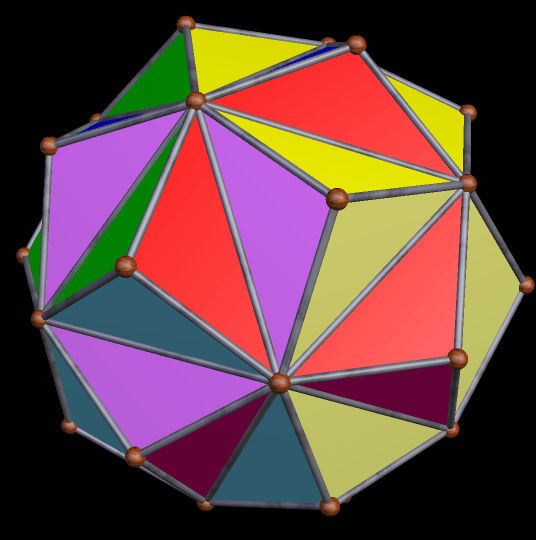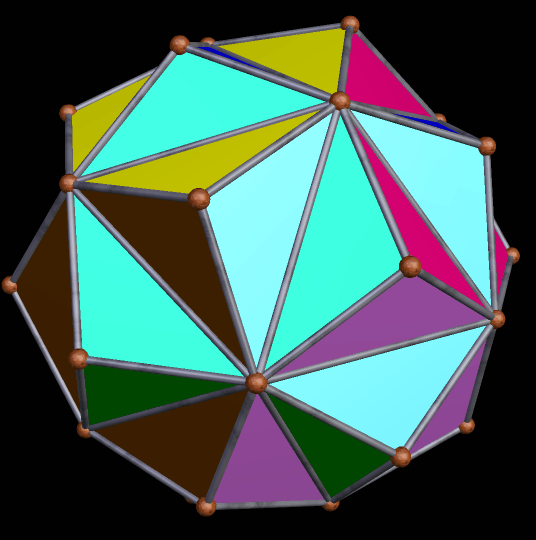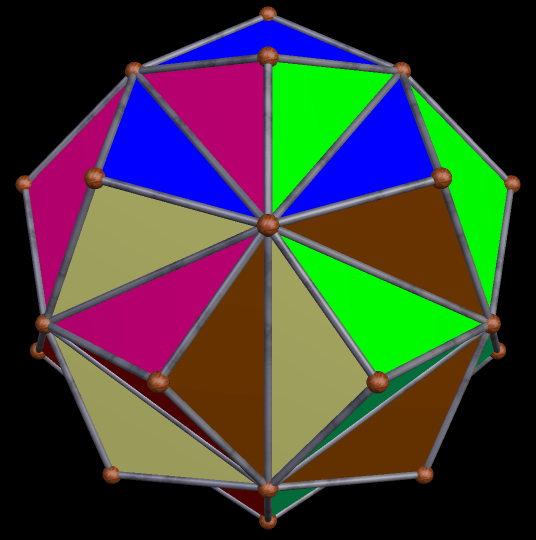
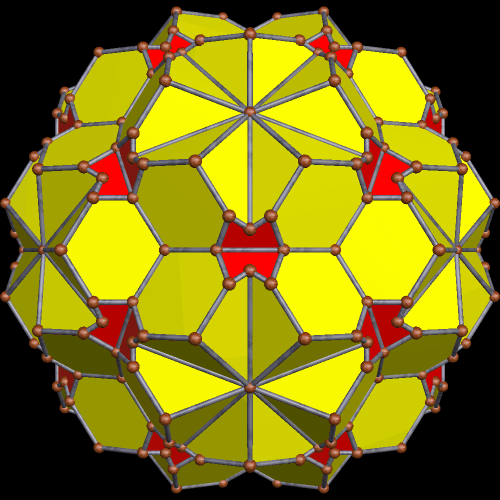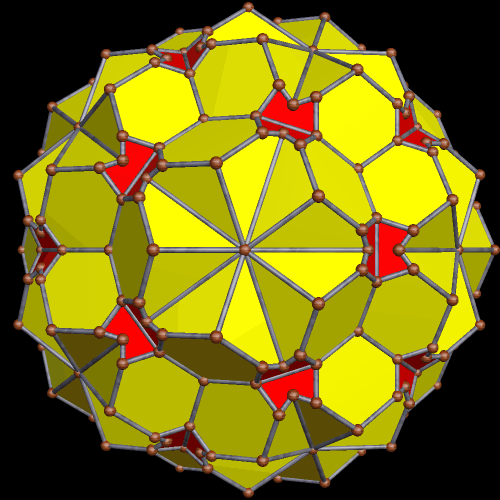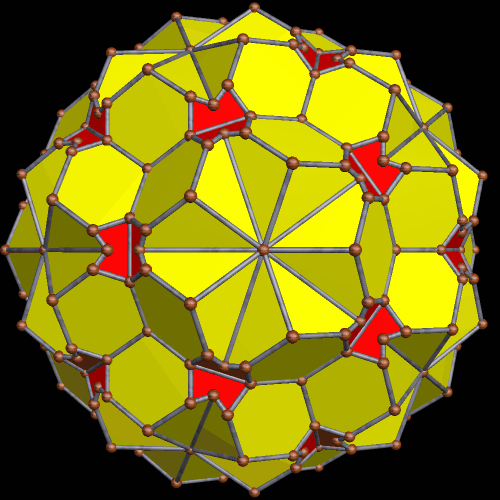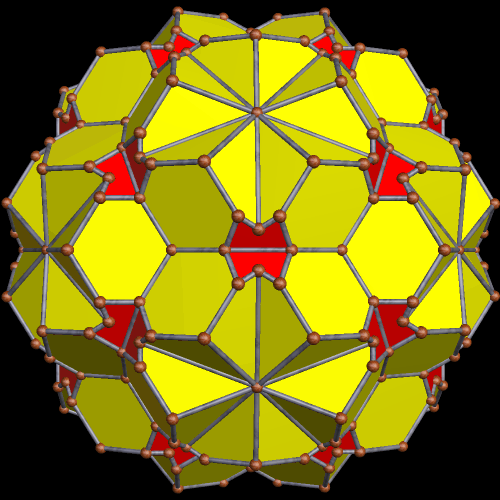
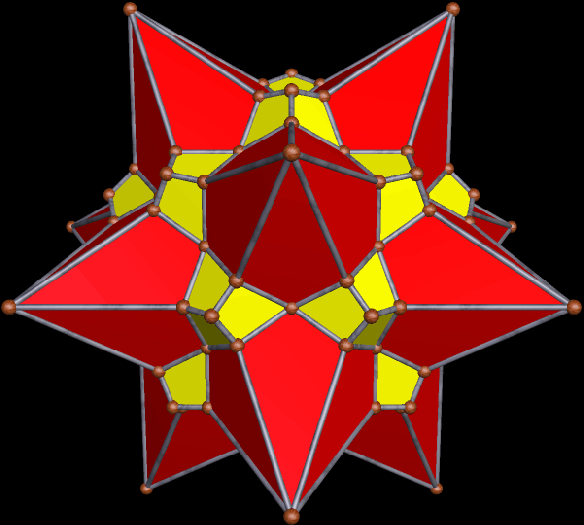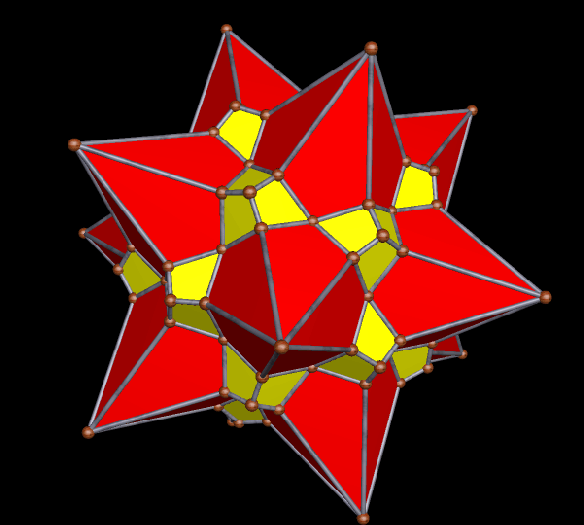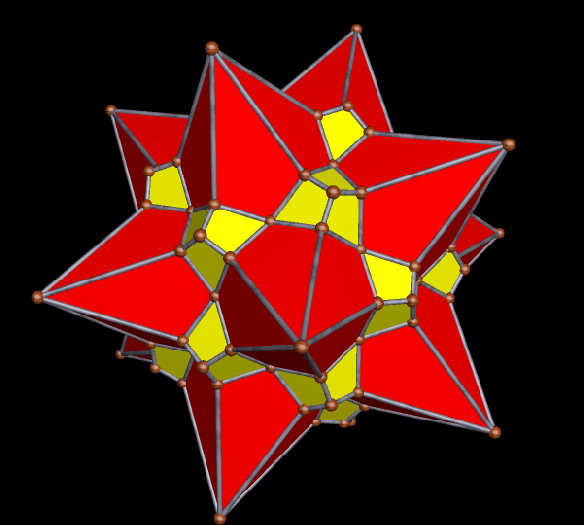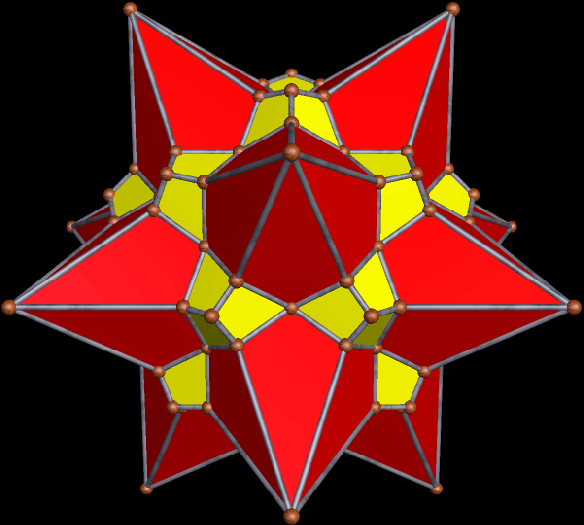
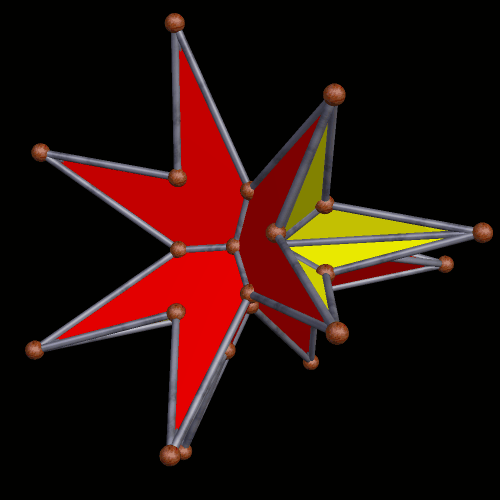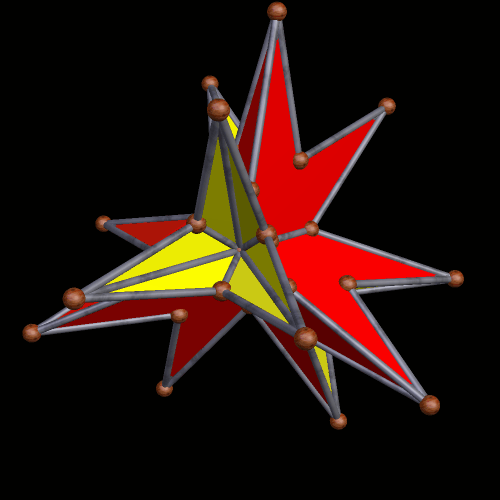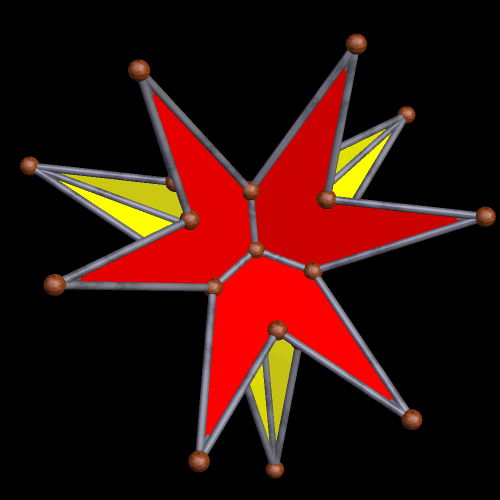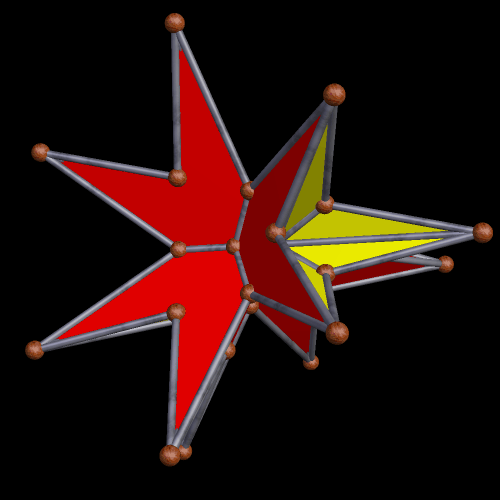
This survey began in the last post, with selections from the first hundred stellations of this Archimedean solid. In this survey of the second hundred stellations, the first one I find noteworthy enough for inclusion here is the 102nd stellation.

A similar figure is the 111th stellation:

There followed a long “desert” when I did not find any that really “grabbed” me . . . and then I came to the 174th stellation.

The fact that it is monocolored, the way I had Stella 4d set, told me immediately that this stellation (the one above) has only one face-type. There are twenty of these faces; they are each equilateral hexagons which “circumscibe,” in a way, the triangular faces of an icosahedron. For this reason, I suspect this is also one of the stellations of the icosahedron; I’m making a mental note to do exactly that.

I also make a second virtual model of the 174th stellation of the rhombicosidodecahedron, with the faces colored in such a way as to make the interpenetrating equilateral hexagons more obvious.

After that interesting stellation, the next one to caught my attention is the 179th stellation.

Next of note, the 182nd stellation is similar to the icosahedron/dodecahedron compound, but with the dodecaheron larger than it is in that compound, so that edges, one from each component polyhedron, do not intersect, but are instead skew. Another way to view it is that the dodecahedron is encasing the icoahedron, but with enough room left for portions of the icosahedron to protrude from the faces of the “dodecahedral cage.”

Next is the 183rd stellation.

Here is the 187th stellation, which is quite similar to the last one shown. The pulsating effect, first seen in the last post above, is an accident, and not discovered until after these images were already made, using Stella 4d, which may be tried here. Why didn’t I re-create the .gifs? Simple: I don’t feel like taking the ~10 minutes each to do so.

The 190th stellation may also be viewed as a dodecahedron, augmented with variations of pentagonal pyramids on each face:

Next, the 191st stellation:

And, after that, the 192nd stellation.

The next stellation which grabbed by attention: the 198th.

Finally, I’ll close this set of highlights from this part of the rhombicosidodecahedron’s stellation-series with that solid’s 199th stellation.

Selections from the First Hundred Stellations of the Rhombicosidodecahedron

Posted on 31 May 2015 by RobertLovesPi

Since shortly after I learned of their existence, I have found the rhombicosidodecahedron to be the most attractive of the Archimedean solids. That’s a personal aesthetic statement, of course, not a mathematical one.

This solid has a long stellation-series. With Stella 4d, the program I used to make these images, it’s easy to simply scroll through them. The stellation of this polyhedron follows these stellation-diagrams; I used Stella 4d to make them as well. You may research, try, or buy this program at this website. The first of these stellation-diagrams is for the planes of the twelve pentagonal faces.

For the planes of the twenty triangular faces, this is the stellation-diagram:

Finally, there are the the planes of the thirty square faces.

The following survey of the first hundred stellations is not intended to be exhaustive; I’m including all those I find worthy of inclusion on subjective aesthetic grounds. The first stellation shown here is actually the 25th stellation of the rhombicosidodecahedron:

Next, the 30th stellation:

The next one is the 33rd stellation.

And next, the 38th stellation.

Here is the 46th stellation:

And the 48th stellation:

Next, the 58th stellation:

And now, the 62nd stellation.

Next is the 85th stellation; it’s also a compound of an icosahedron (blue), and a yellow polyhedron I have not yet identified, except as the nth stellation of something. This I know: I have seen the yellow polyhedron before. If you happen to know what it is, the identify it in a comment.

The next stellation shown is the next one in the series, the 86th. It demonstrates a phenomenon I have observed, but cannot explain, and that is the tendency, in sequences of stellations, to have a large number of similar stellations in a row, followed by a sudden, much more extreme change in appearance, from one stellation to the next, as seen here. It’s a phenomenon which I would like to better understand.

To be continued, with selections from the next hundred stellations….

The Final Stellation of the Great Rhombicosidodecahedron, Together with Its Dual

Posted on 25 May 2015 by RobertLovesPi

In the last post, several selections from the stellation-series of the great rhombicosidodecahedron (which some people call the truncated icosidodecahedron) were shown. It’s a long stellation-series — hundreds, or perhaps thousands, or even millions, of stellations long (I didn’t take the time to count them) — but it isn’t infinitely long. Eventually, if repeatedly stellating this polyhedron, one comes to what is called the “final stellation,” which looks like this:

Stellation-series “wrap around,” so if this is stellated one more time, the result is the (unstellated) great rhombicosidodecahedron. In other words, the series starts over.

The dual of the great rhombicosidodecahedron is called the disdyakis triacontahedron. The reciprocal function of stellation is faceting, so the dual of the figure above is a faceted disdyakis triacontahedron. Here is this dual:

To complicate matters further, there is more than one set of rules for stellation. For an explanation of this, I refer you to this Wikipedia page. In this post, and the one before, I am using what are known as the “fully supported” rules.

Both these images were made using Stella 4d, software you can buy, or try for free, right here. When stellating polyhedra using this program, it can be set to use different rules for stellation. I usually leave it set for the fully supported stellation criteria, but other polyhedron enthusiasts have other preferences.

Selections from the Stellation-Series of the Great Rhombicosidodecahedron

Posted on 25 May 2015 by RobertLovesPi

The great rhombicosidodecahedron, also known as the truncated icosidodecahedron, has a long and complex stellation series. Here are some highlights from that series, chosen using aesthetic, rather than mathematical, criteria.

All these virtual models were made using Stella 4d, which you can try and/or buy here.

Selections from the Stellation-Series of the Icosidodecahedron

Posted on 4 May 2015 by RobertLovesPi

The icosidodecahedron has a long and interesting stellation-series, and you can see the whole thing using Stella 4d, the program I used to make the rotating .gifs here. Rather than keep the scale the same in each frame, I set the program to make the polyhedron as large as possible, while still fitting in the image-box. This creates the illusion that the polyhedra below are “breathing.”

The polyhedron above is the 20th stellation of the icosidodecahedron — the one that appeared as the sole image in the last post here, but with completely different colors. The next one shown is the 31st stellation.

The 55th stellation is immediately above, while the next one is the 69th.

The 84th stellation is immediately above, while the next one is the 89th.

The 106th stellation is immediately above, while the next one is the the 110th.

The 135th stellation is immediately above, while the next one, which is chiral, is the 157th.

Glimpses of the Invisible

Posted on 3 May 2015 by RobertLovesPi

Created using Stella 4d, available here, by multiple stellations of a black icosidodecahedron, rendered as a rotating figure, against a black background.

A Stellated Polyhedron, Mostly Blue

Posted on 14 April 2015 by RobertLovesPi

This is the first stellation of the second polyhedron seen in the post just before this one, but with the color-scheme changed, on the grounds that I like blue. If you’d like to know more about how this polyhedron was created, I refer you to that post. Stella 4d was used to make these: software you can try right here.

Stellating the Great Dodecahedron, by Twentieths, to Beethoven’s Ninth

Posted on 12 April 2015 by RobertLovesPi

In this video, the great dodecahedron is stellated, by twentieths, into the great stellated dodecahedron, while a selection from Ludwig van Beethoven’s Ninth Symphony plays. The images for this video were created using Stella 4d, a program you can try for yourself (free trial download available), right here: http://www.software3d.com/Stella.php.

The Twelfth Stellation of the Triakis Tetrahedron

Posted on 20 January 2015 by RobertLovesPi

Created with Stella 4d, available here.

The Final Stellation of the Icosahedron

Posted on 9 January 2015 by RobertLovesPi

This is what you get if you stellate an icosahedron seventeen times. The eighteenth stellation “loops” back around to the original figure, the icosahedron. For this reason, the figure above is often called “the final stellation of the icosahedron,” as well as “the complete icosahedron.” Its faces are twenty irregular star enneagons, of the type shown below. The red areas are the “facelets” which can be seen, while the other parts of the star enneagon are hidden inside the figure.