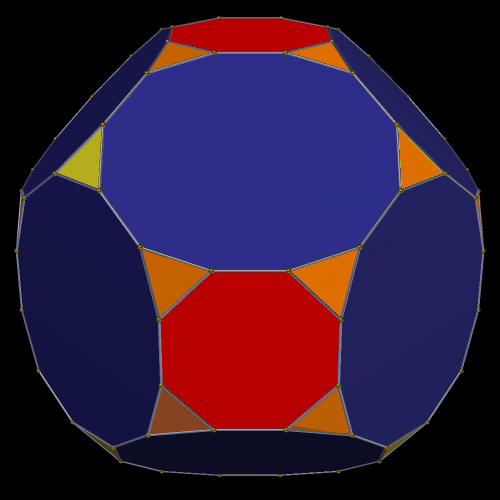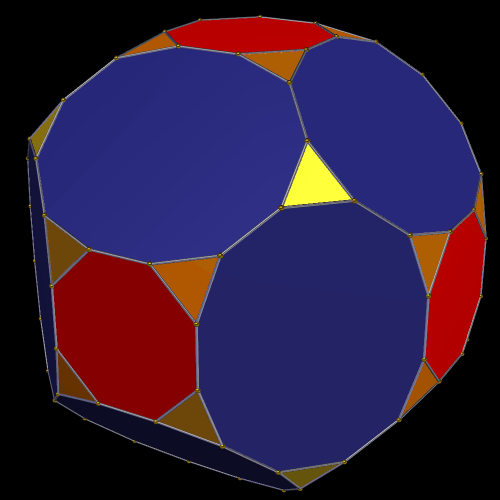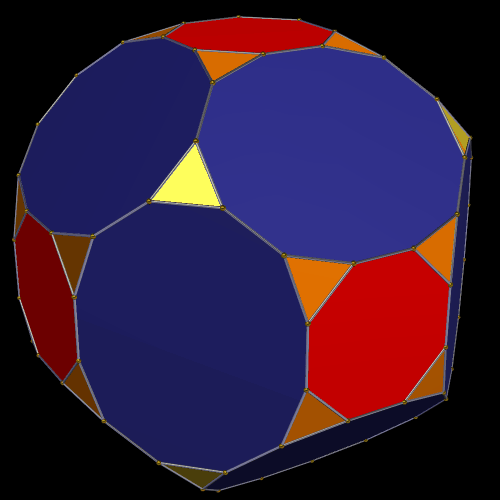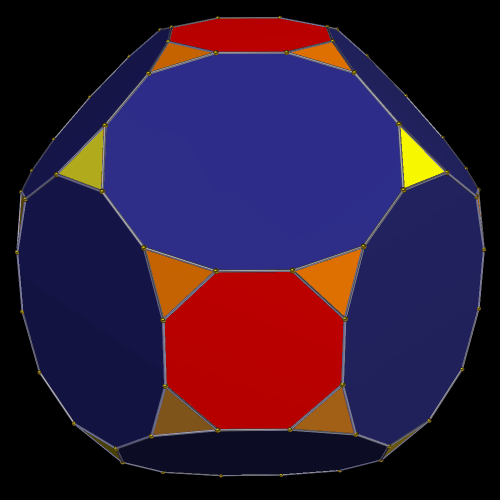
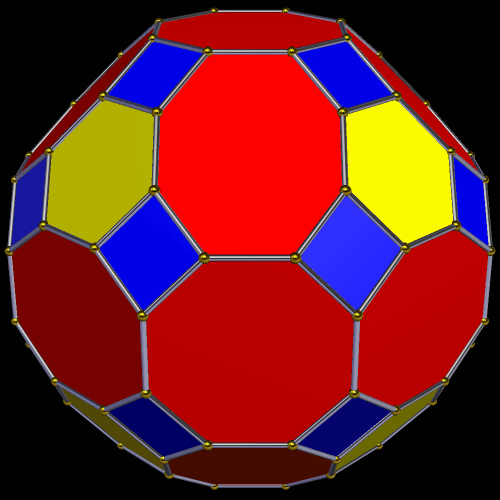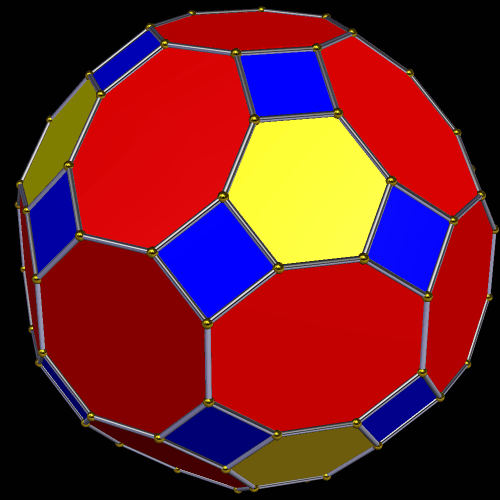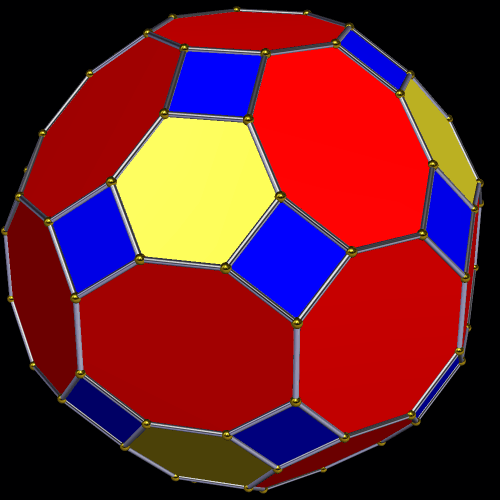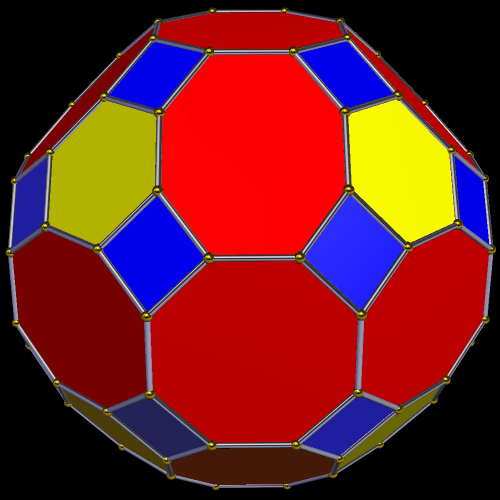
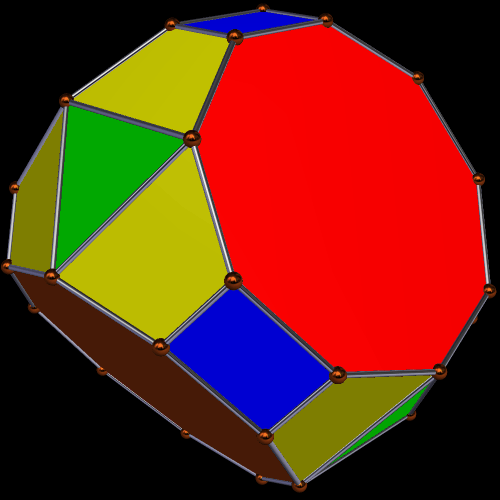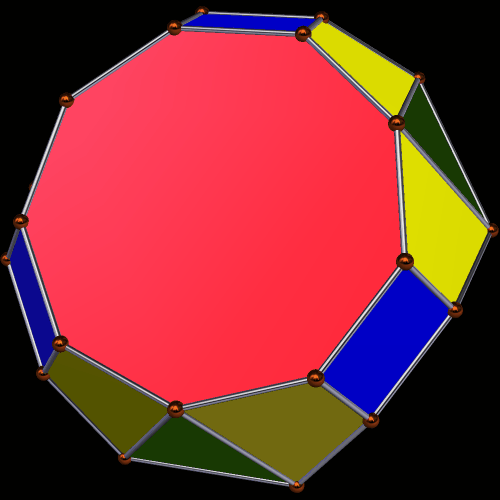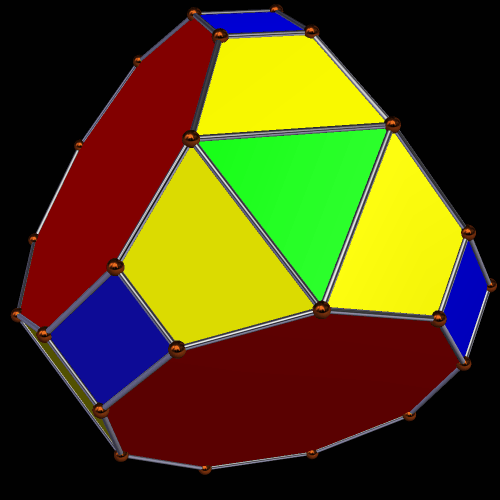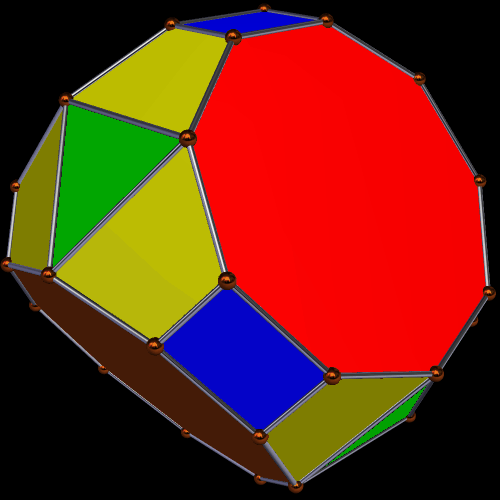
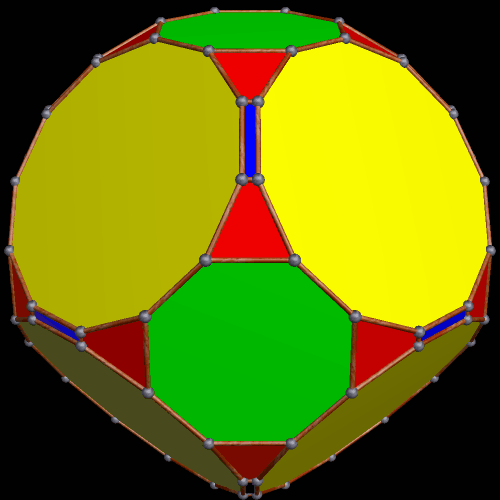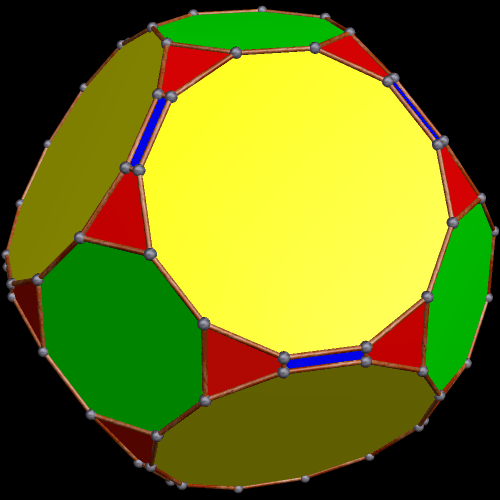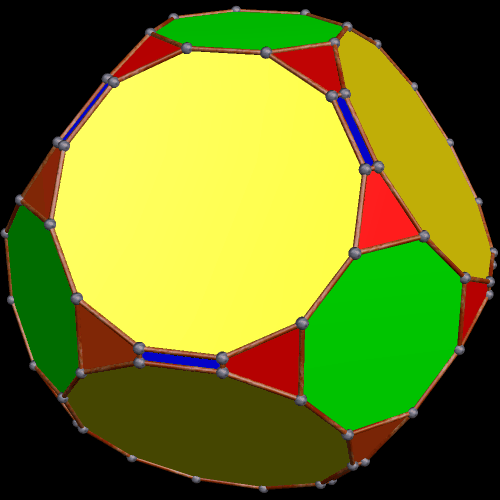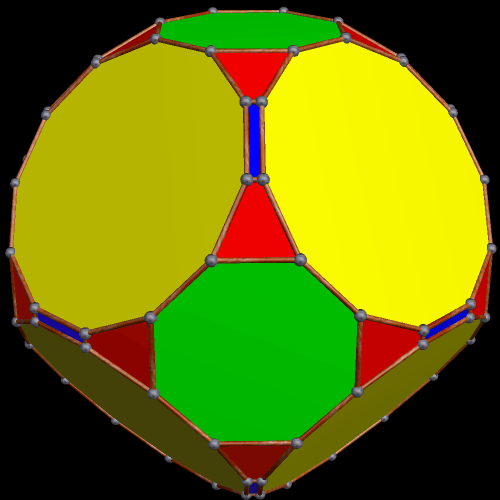
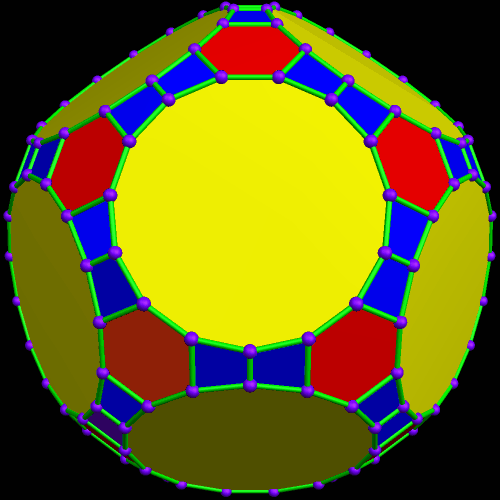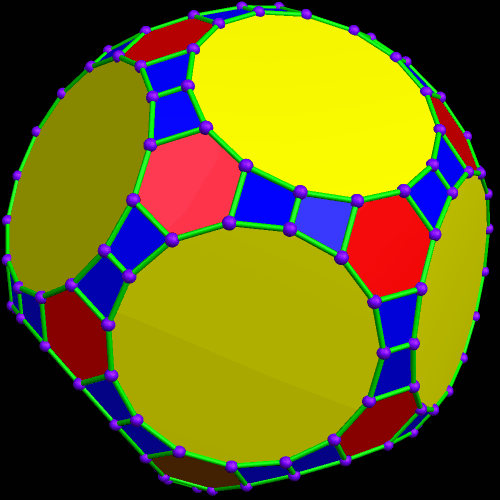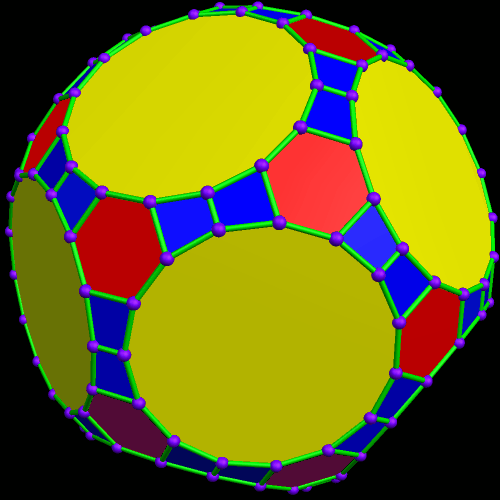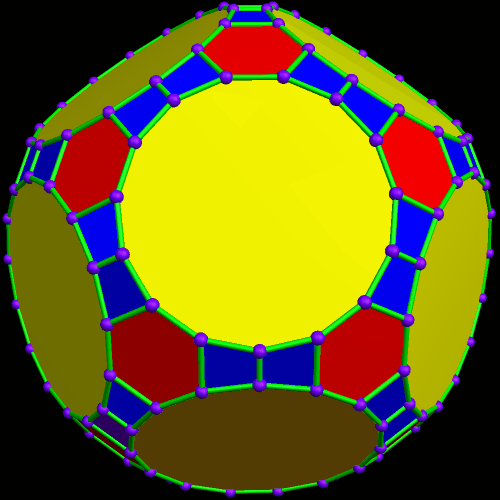
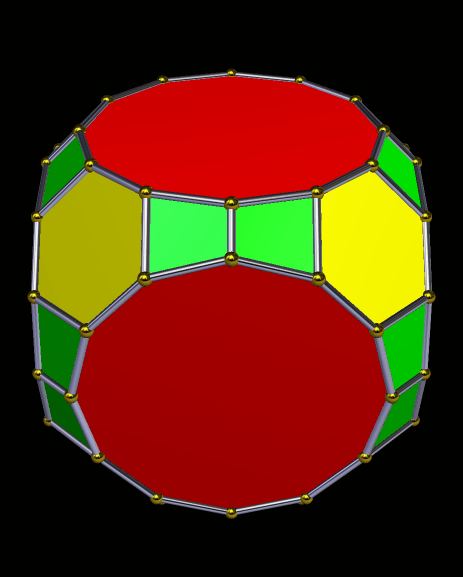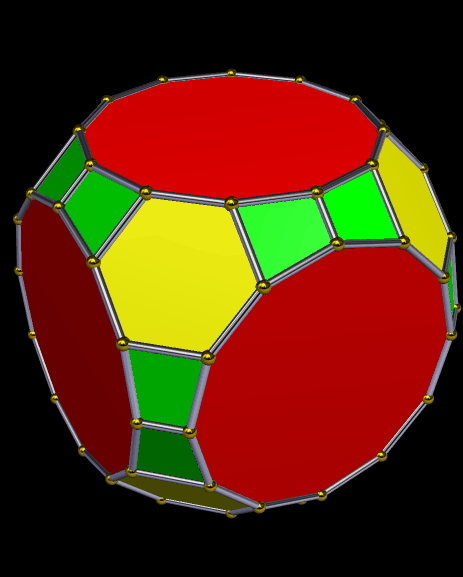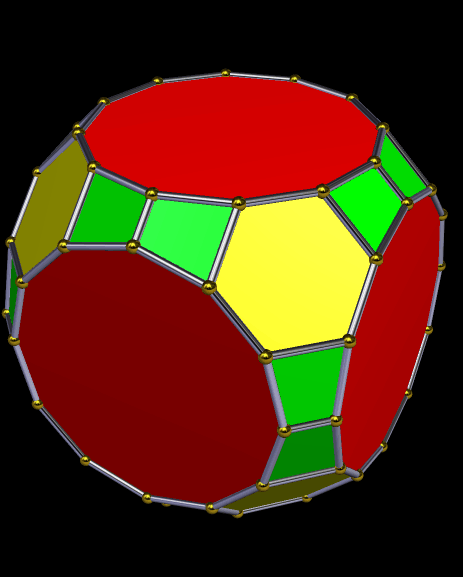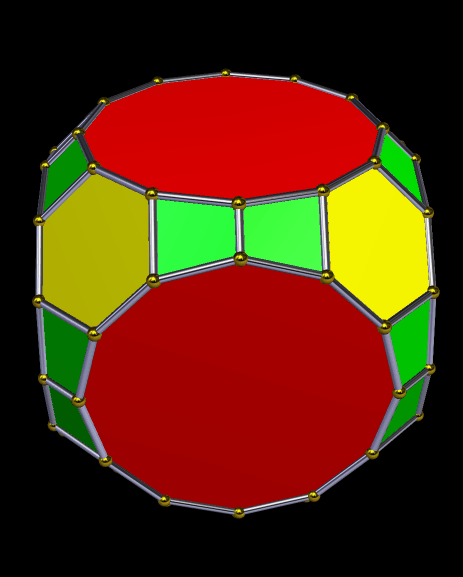
Dave Smith discovered the polyhedron in the last post here, shown below, with the faces hidden, to reveal how the edges appear on the back side of the figure, as it rotates. (Other views of it may be found here.)

So far, all of Smith’s “bowtie” polyhedral discoveries have been convex, and have had only two types of face: regular polygons, plus isosceles trapezoids with three equal edge lengths — a length which is in the golden ratio with that of the fourth side, which is the shorter base.

He also found another solid: the second of Smith’s polyhedral discoveries in the class of bowtie symmetrohedra. In it, each of the four pentagonal faces of the original discovery is augmented by a pentagonal pyramid which uses equilateral triangles as its lateral faces. Here is Smith’s original model of this figure, in which the trapezoids are invisible. (My guess is that these first models, pictures of which Dave e-mailed to me, were built with Polydrons, or perhaps Jovotoys.)

With Stella 4d (available here), the program I use to make all the rotating geometrical pictures on this blog, I was able to create a version (by modifying the one created by via collaboration between five people, as described in the last post) of this interesting icositetrahedron which shows all four trapezoidal faces, as well as the twenty triangles.

Here is another view: trapezoids rendered invisible again, and triangles in “rainbow color” mode.

It is difficult to find linkages between the tetrapentagonal octahedron Smith found, and other named polyhedra (meaning  I haven’t yet figured out how), but this is not the case with this interesting icositetrahedron Smith found. With some direct, Stella-aided polyhedron-manipulation, and a bit of research, I was able to find one of the Johnson solids which is isomorphic to Smith’s icositetrahedral discovery. In this figure (J90, the disphenocingulum), the trapezoids of this icositetrahedron are replaced by squares. In the pyramids, the triangles do retain regularity, but, to do so, the pentagonal base of each pyramid is forced to become noncoplanar. This can be difficult to see, however, for the now-skewed bases of these four pyramids are hidden inside the figure.

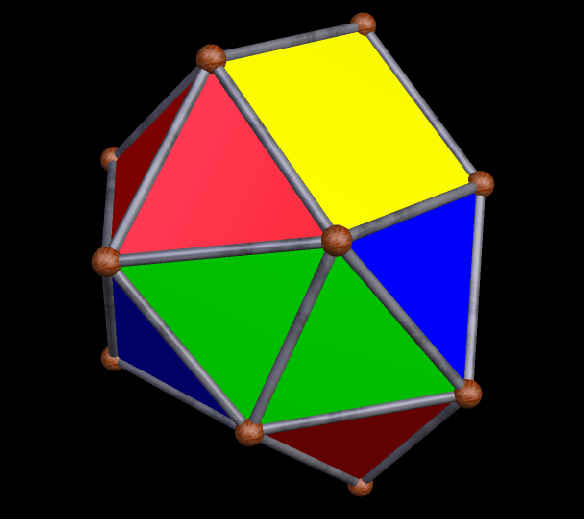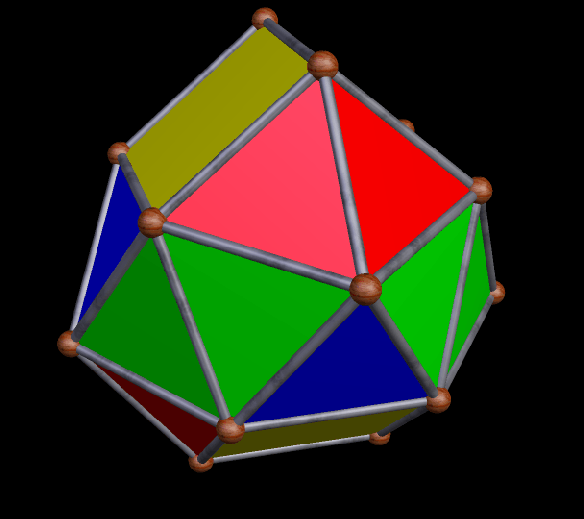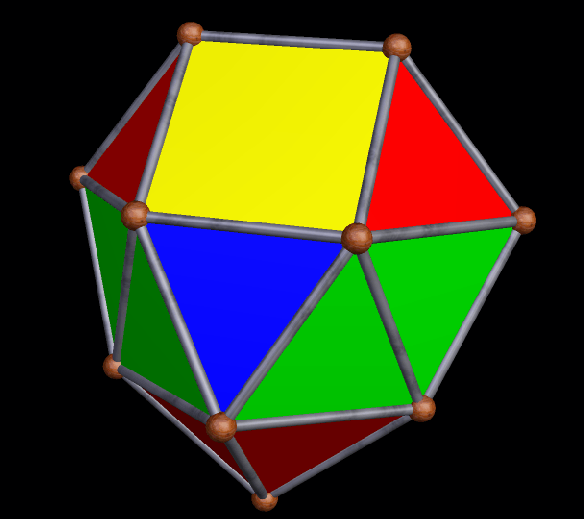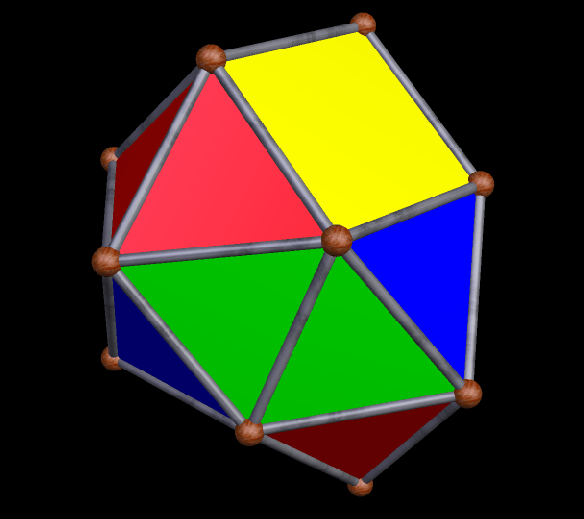
Both of these solids Smith found, so far (I am confident that more await discovery, by him or by others) are also golden polyhedra, in the sense that they have two edge lengths, and these edge lengths are in the golden ratio. The first such polyhedron I found was the golden icosahedron, but there are many more — for example, there is more than one way to distort the edge lengths of a tetrahedron to make golden tetrahedra.

To my knowledge, no ones knows how many golden polyhedra exist, for they have not been enumerated, nor has it even been proven, nor disproven, that their number is finite. At this point, we simply do not know . . . and that is a good way to define areas in mathematics in which new work remains to be done. A related definition is one for a mathematician: a creature who cannot resist a good puzzle.