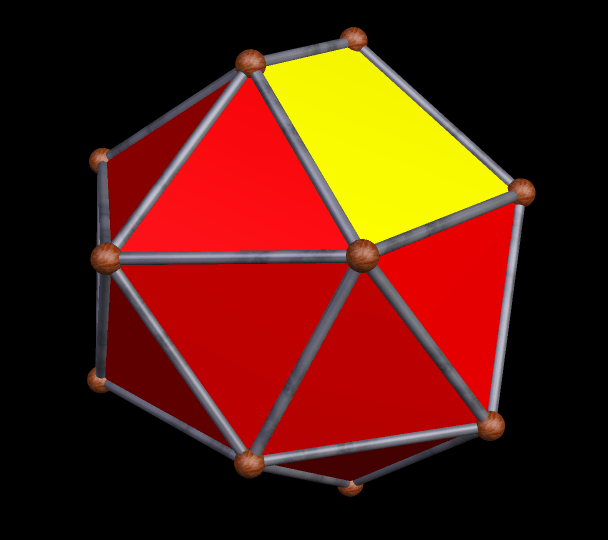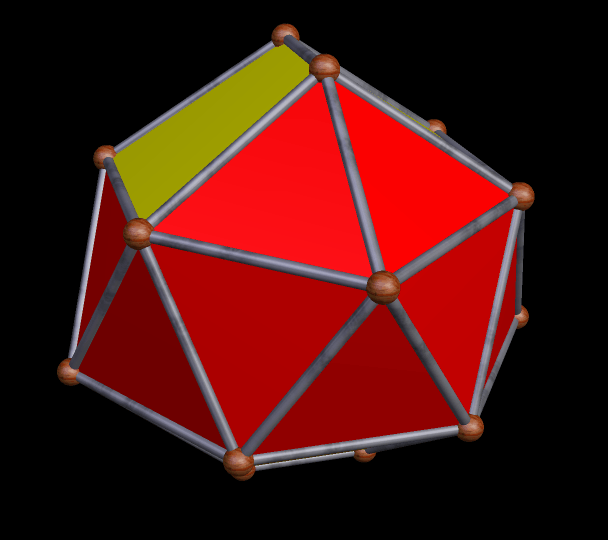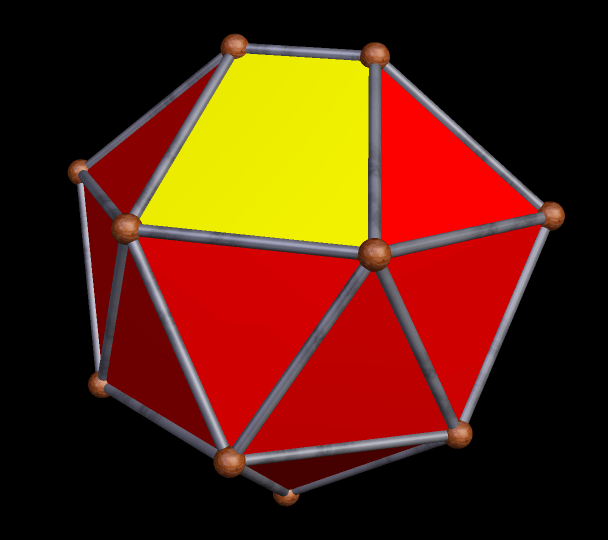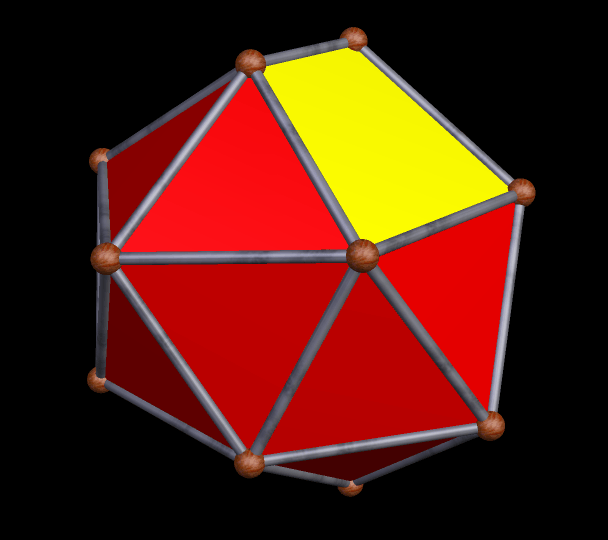
This 24-faced polyhedron, which has pyritohedral symmetry, was formed by repeatedly tetstelling a rhombic triacontahedron, using Stella 4d: Polyhedron Navigator. If you wish, you can try this program for free right here.
Tag Archives: trapezoid
Two Chiral Polyhedra Which Feature Many Trapezoidal Faces
The polyhedron above is a faceted pentagonal icositetrahedron. The unfaceted, normal pentagonal icositetrahedron is the dual of the snub cube.
The solid below is a faceted pentagonal hexecontahedron, which, in unfaceted form, is the dual of the snub dodecahedron.
I made both of these models with Stella 4d, a program you may try for free at http://www.software3d.com/Stella.php.
Trapezoid Tessellation
Image
Tessellation of Isosceles Trapezoids
Image

A Chiral Polyhedron Made of Kites and Triangles, Along with Its Dual, Made of Triangles and Isosceles Trapezoids
To make this polyhedron using Stella 4d (available here), one starts with the icosahedron, drops the symmetry of the model down from icosahedral to tetrahedral, and then stellates it once. The result is a chiral solid featuring four triangular faces and twelve kites:

The dual of this polyhedron, which is also chiral, has four triangular faces, and twelve faces which are isosceles trapezoids. It is a type of faceted dodecahedron — a partial faceting, meaning it is made without using all of the dodecahedron’s vertices.

The Second of Dave Smith’s “Bowtie” Polyhedral Discoveries, and Related Polyhedra
Dave Smith discovered the polyhedron in the last post here, shown below, with the faces hidden, to reveal how the edges appear on the back side of the figure, as it rotates. (Other views of it may be found here.)
So far, all of Smith’s “bowtie” polyhedral discoveries have been convex, and have had only two types of face: regular polygons, plus isosceles trapezoids with three equal edge lengths — a length which is in the golden ratio with that of the fourth side, which is the shorter base.
He also found another solid: the second of Smith’s polyhedral discoveries in the class of bowtie symmetrohedra. In it, each of the four pentagonal faces of the original discovery is augmented by a pentagonal pyramid which uses equilateral triangles as its lateral faces. Here is Smith’s original model of this figure, in which the trapezoids are invisible. (My guess is that these first models, pictures of which Dave e-mailed to me, were built with Polydrons, or perhaps Jovotoys.)
With Stella 4d (available here), the program I use to make all the rotating geometrical pictures on this blog, I was able to create a version (by modifying the one created by via collaboration between five people, as described in the last post) of this interesting icositetrahedron which shows all four trapezoidal faces, as well as the twenty triangles.
Here is another view: trapezoids rendered invisible again, and triangles in “rainbow color” mode.
It is difficult to find linkages between the tetrapentagonal octahedron Smith found, and other named polyhedra (meaning I haven’t yet figured out how), but this is not the case with this interesting icositetrahedron Smith found. With some direct, Stella-aided polyhedron-manipulation, and a bit of research, I was able to find one of the Johnson solids which is isomorphic to Smith’s icositetrahedral discovery. In this figure (J90, the disphenocingulum), the trapezoids of this icositetrahedron are replaced by squares. In the pyramids, the triangles do retain regularity, but, to do so, the pentagonal base of each pyramid is forced to become noncoplanar. This can be difficult to see, however, for the now-skewed bases of these four pyramids are hidden inside the figure.
Both of these solids Smith found, so far (I am confident that more await discovery, by him or by others) are also golden polyhedra, in the sense that they have two edge lengths, and these edge lengths are in the golden ratio. The first such polyhedron I found was the golden icosahedron, but there are many more — for example, there is more than one way to distort the edge lengths of a tetrahedron to make golden tetrahedra.
To my knowledge, no ones knows how many golden polyhedra exist, for they have not been enumerated, nor has it even been proven, nor disproven, that their number is finite. At this point, we simply do not know . . . and that is a good way to define areas in mathematics in which new work remains to be done. A related definition is one for a mathematician: a creature who cannot resist a good puzzle.
The Beginning of an Attempt to Create an Aperiodic Tessellation of Golden Trapezoids
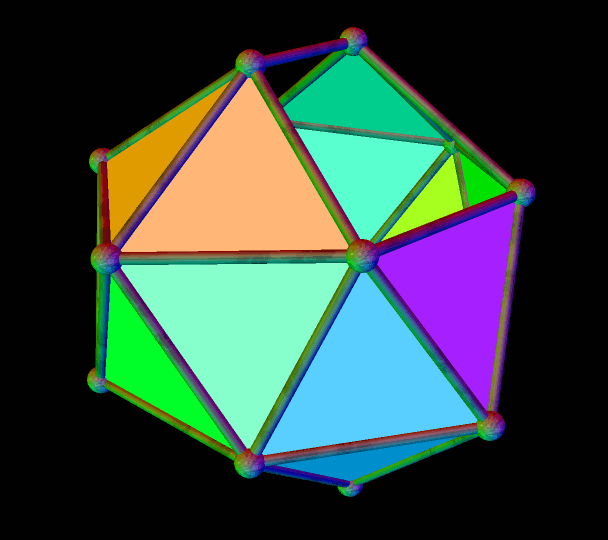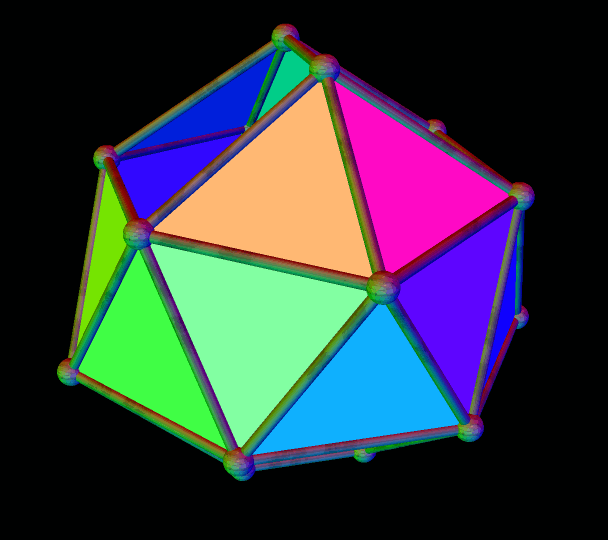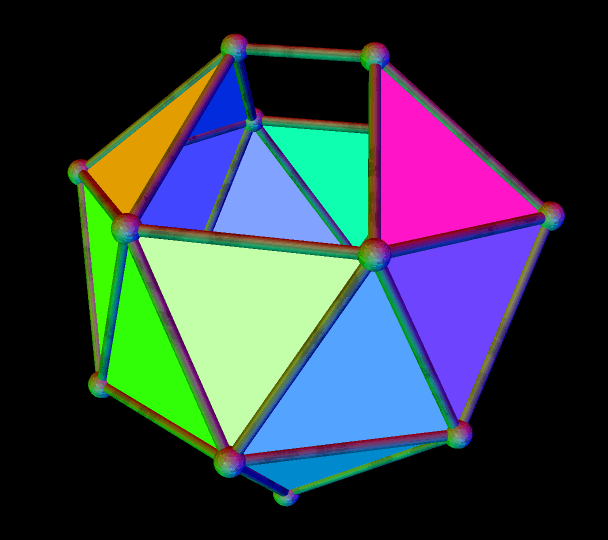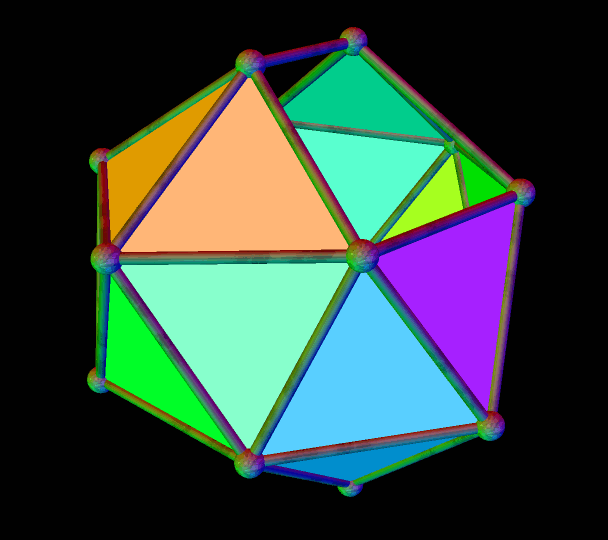
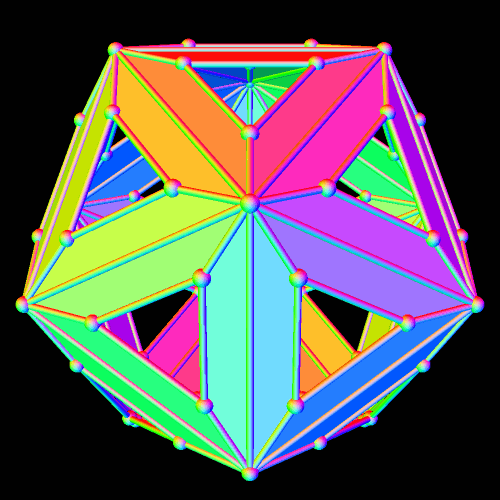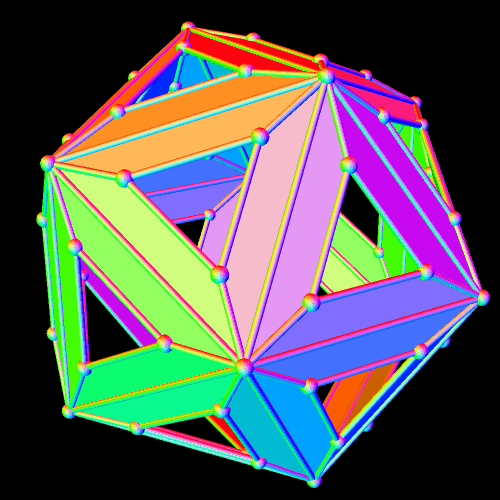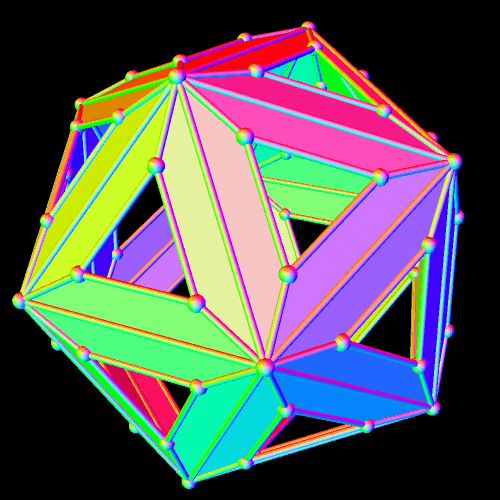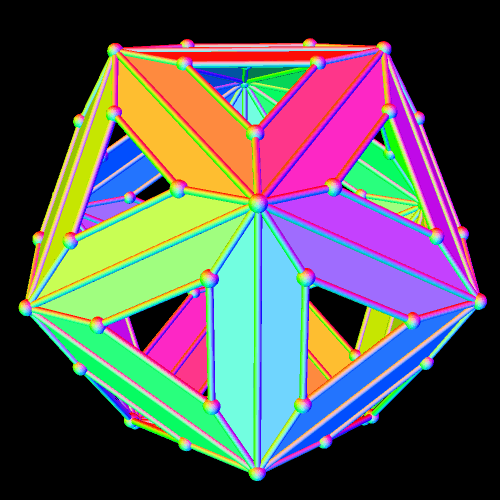
A Polyhedral Demonstration of the Fact That Twenty Times Four Is Eighty
The Platonic solid known as the icosahedron has twenty triangular faces. This polyhedron resembles the icosahedron, but with each of the icosahedron’s triangles replaced by a panel of four faces: three isosceles trapezoids surrounding a central triangle. Since (20)(4) = 80, it is possible to know that this polyhedron has eighty faces — without actually counting them.
To let you see the interior structure of this figure, I next rendered its triangular faces invisible, to form “windows,” and then, just for fun, put the remaining figure in “rainbow color mode.”
 I perform these manipulations of polyhedra using software called Stella 4d. If you’d like to try this program for yourself, the website to visit for a free trial download is http://www.software3d.com/Stella.php.
I perform these manipulations of polyhedra using software called Stella 4d. If you’d like to try this program for yourself, the website to visit for a free trial download is http://www.software3d.com/Stella.php.
This Space Station for Geometricians Has, as Outer Hulls, Twelve Trapezoids, and Six Parallelograms with One Square Window / Docking Port Each
I can’t think of any good reasons for geometricans not to have their own space station, and I know what we’d do there: we’d work on geometry (also known informally as “playing with shapes”).
My suggestion for this space station’s design was created with Stella 4d, and you may find that program (to try or guy) here: http://www.software3d.com/Stella.php.
Dodecahedral Polyhedron Featuring Regular Icosagons, Regular Hexagons, Rectangles, and Isosceles Trapezoids
Image
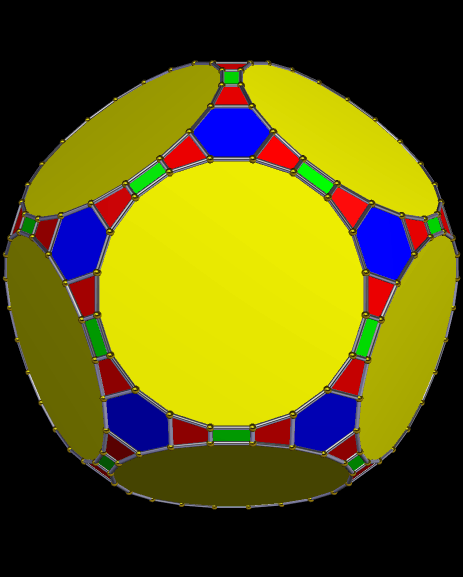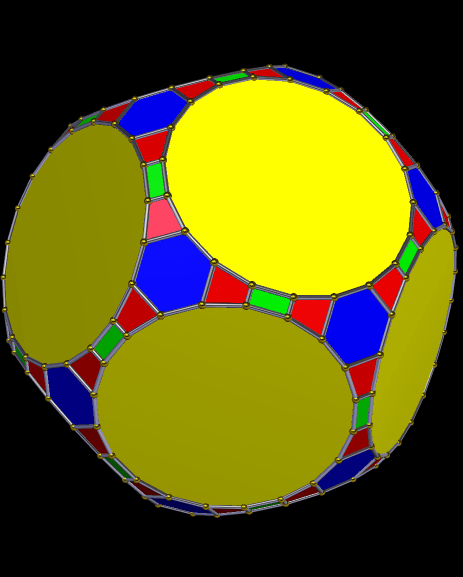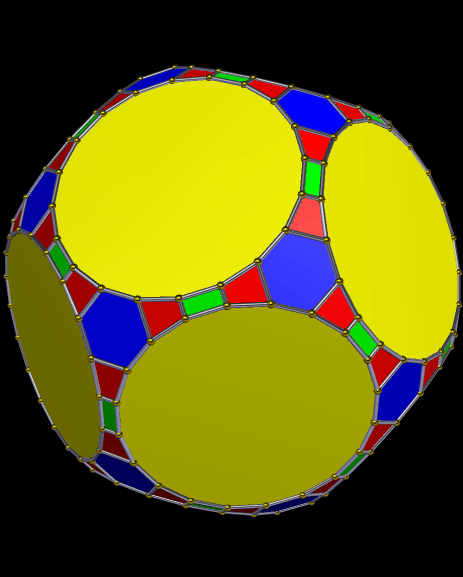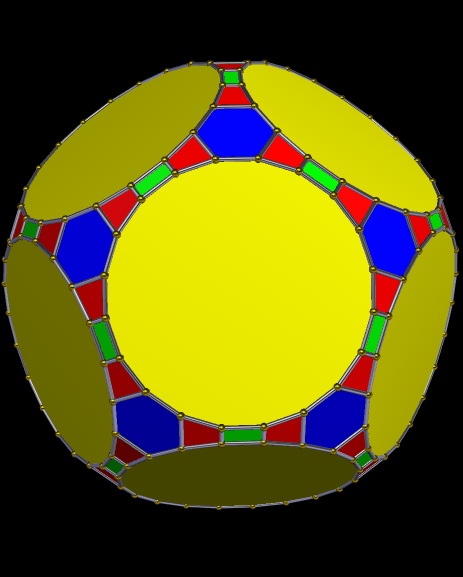
Created with Stella 4d, software you can try and/or buy at http://www.software3d.com/Stella.php.