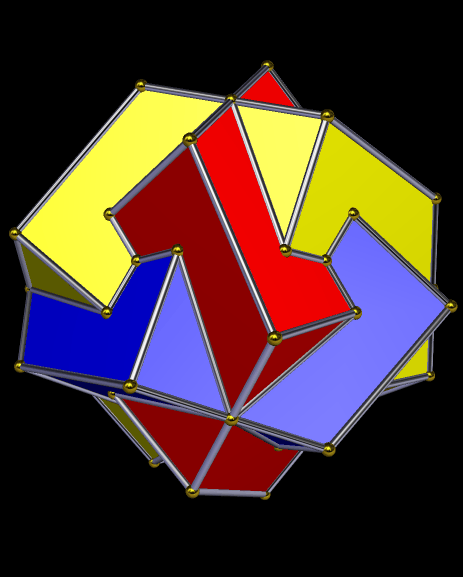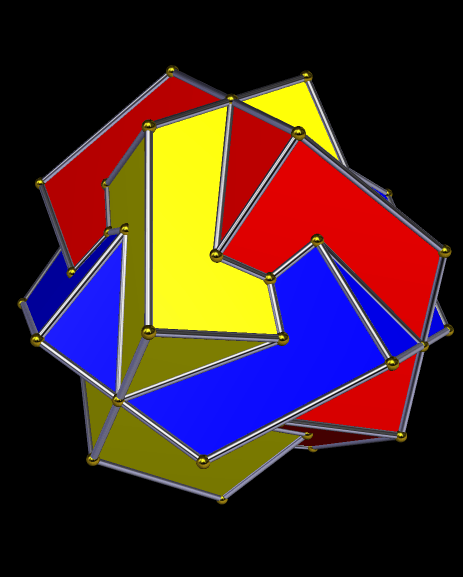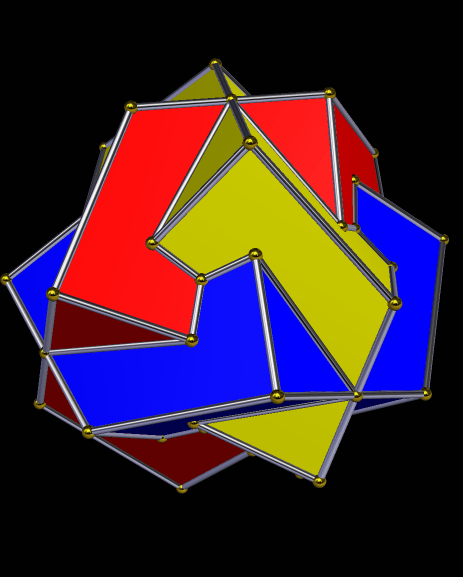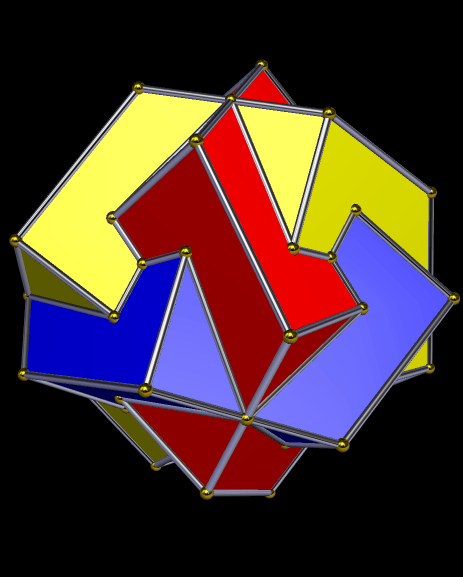
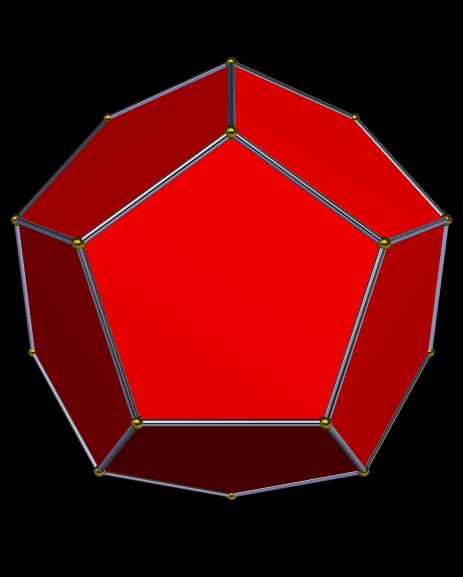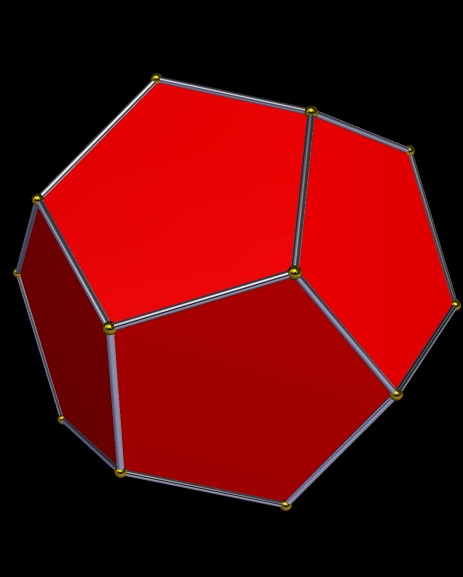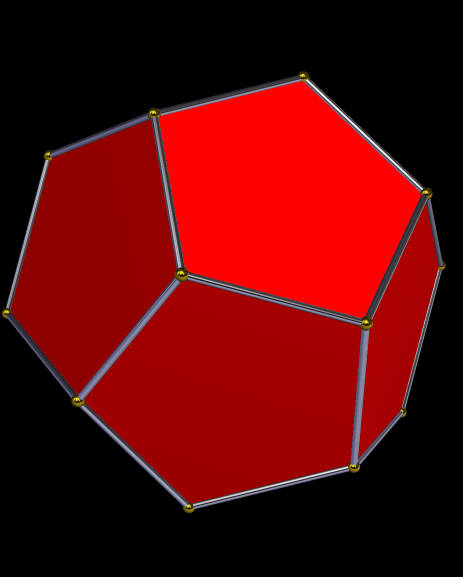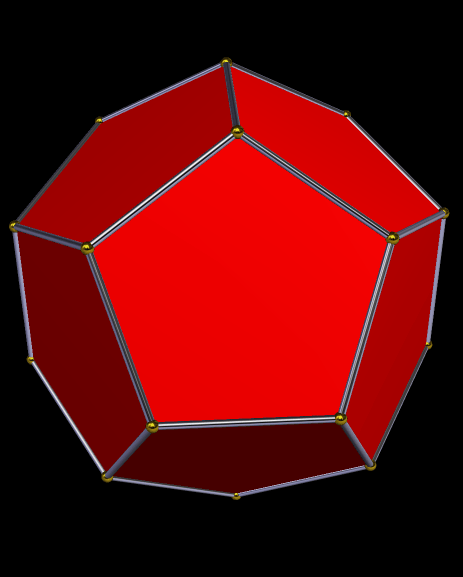
Years ago, I split a dodecahedron into four panels of pentagons, rotated the pentagon-panels and moved them outward from the center, and did so just the right amount to create gaps that could be filled with triangles. Thus was named the tetrated dodecahedron, which you can read more about here: https://en.wikipedia.org/wiki/Tetrated_dodecahedron
The choice of word “tetrated” was somewhat unfortunate, for tetration already exists in mathematics, as a means of expressing very large numbers, and which I shall not explain here. I didn’t learn this until much later, though, and by that time, it was too late to turn “tetrate” into something else. It had come to mean an operation one does on a polyhedron: break it into four multi-face panels, move them out and rotate them just enough, and fill the resulting gaps with triangles.
As such, “tetrate” can, in the geometrical sense, be modified for differing numbers of panels of multiple faces from a polyhedron. Consider the pentagonal icositetrahedron, the dual of the snub cube. Here, it has been split into six panels, and then each panel moved out from the center and rotated, with triangles filling the gaps. The triangles differ between color-groups slightly, but are close to equilateral, except for the ones shown in green, which simply are equilateral.
(Image created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)