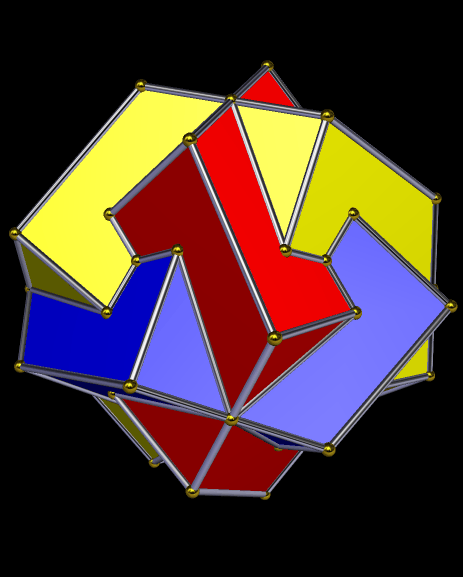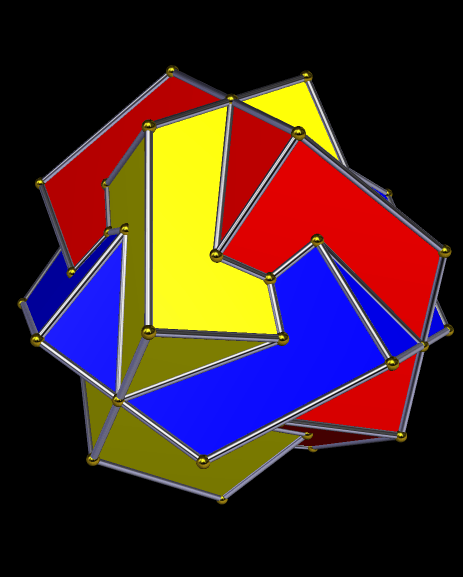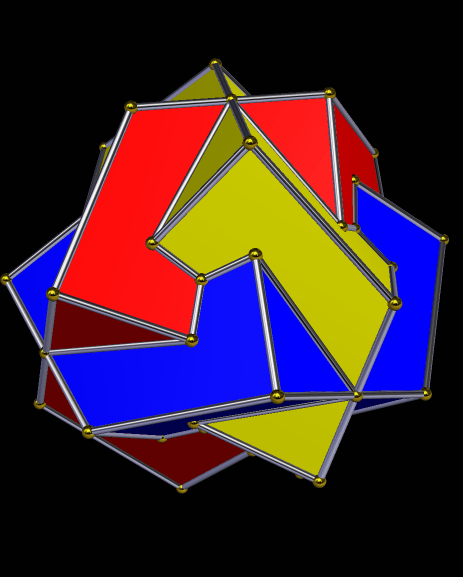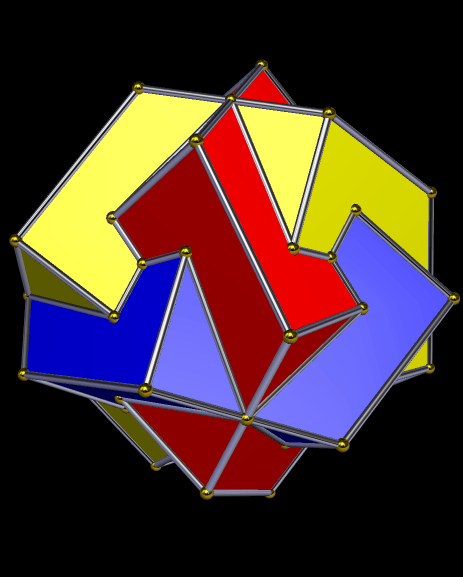
(Image created with Stella 4d — software you can try yourself at http://www.software3d.com/Stella.php.)
Share this:
- Share on Bluesky (Opens in new window) Bluesky
- Email a link to a friend (Opens in new window) Email
- Share on Facebook (Opens in new window) Facebook
- Share on Mastodon (Opens in new window) Mastodon
- Share on Nextdoor (Opens in new window) Nextdoor
- Share on Pinterest (Opens in new window) Pinterest
- Share on Pocket (Opens in new window) Pocket
- Print (Opens in new window) Print
- Share on Reddit (Opens in new window) Reddit
- Share on Telegram (Opens in new window) Telegram
- Share on Threads (Opens in new window) Threads
- Share on Tumblr (Opens in new window) Tumblr
- Share on WhatsApp (Opens in new window) WhatsApp
- Share on X (Opens in new window) X