Both of these were made using Stella 4d: Polyhedron Navigator. It’s available at http://www.software3d.com/Stella.php.
If you want to enlarge this second image, simply click on it.
I created this using Stella 4d, which is available (including a free trial download) at http://www.software3d.com/Stella.php. With adjustments in edge lengths to make the bond lengths correct, this would be the shape of a C180 fullerene molecule.
If the thirty-two faces of the truncated icosahedron are hidden, and only the sixty extra hexagons are visible, this polyhedron looks like this:
In “rainbow color mode,” it has an even more interesting appearance:
The top image here is of a zonish polyhedron based on adding zones along the five-fold symmetry axes of a rhombicosidodecahedron. All its edges are the same length, and its 62 faces include thirty elongated octagons, twelve regular pentagons, and twenty triangles. All of its edges have the same length.
The edges of this next polyhedron are also all of the same length. It was made in the same way, except that zones were added along both three- and five-fold symmetry axes of a rhombicosidodecahedron. Its 182 faces include thirty elongated dodecagons, twenty triangles, twelve regular pentagons, sixty squares, and sixty rhombi.
If only the three-fold symmetry axes are used to make a zonish polyhedron from a rhombicosidodecahedron, this next polyhedron, also with all edge lengths equal, is the result. It also has 182 faces, and they are of the same type as in the one immediately before, except that thirty elongated octagons replace the dodecagons from that polyhedron.
A rhombicosidodecahedron also has two-fold symmetry axes. If only those axes are used to make a zonish rhombicosidodecahedron, this next polyhedron is the result: a modified form of the great rhombicosidodecahedron, with unequal edge lengths.
If the two- and three-fold symmetry axes are both used, the result, once again, is a 182-faces polyhedron, but it also has unequal edge lengths, and none of its faces are regular polygons. It is shown below. There are twelve decagons, sixty rectangles, sixty hexagons of one type, twenty hexagons of another type, and thirty octagons.
Another possible combination is to use the two- and five-fold symmetry axes to create a zonish rhombicosidodecahedron. This yields a polyhedron with 122 faces, with all except the sixty squares being irregular. The other faces are twelve decagons, thirty octagons, and twenty hexagons:
Finally, there is one last combination — using the two-, three-, and five-fold symmetry axes, all at once. Here’s what it looks like:
As one should expect, this produces a zonish polyhedron with more faces than any of the earlier ones shown above: 242 in all. As in the last one shown, only the sixty squares are regular, although the sixty pink hexagons are at least equilateral. There are also sixty rectangles, twenty hexagons of a second type, thirty dodecagons, and twelve decagons.
All of these zonish rhombicosidodecahedra were created using Stella 4d, software available at http://www.software3d.com/Stella.php.
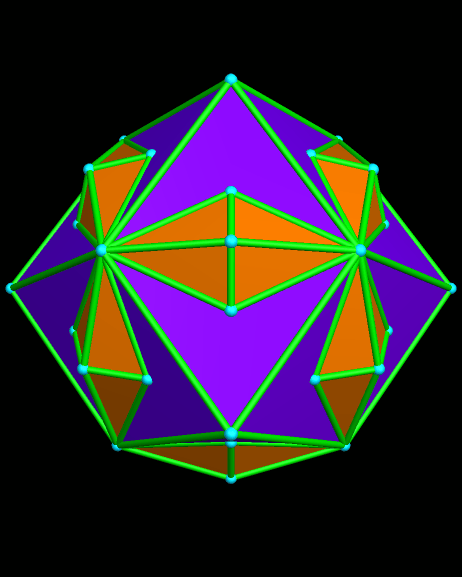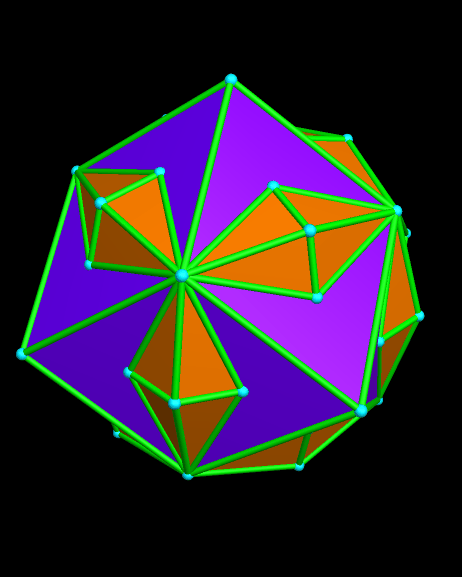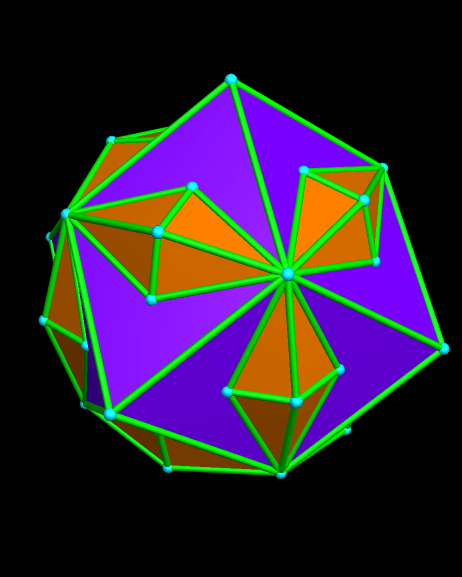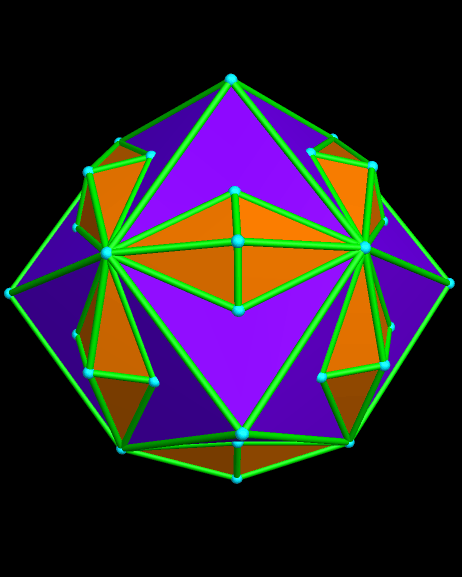
I created this using Stella 4d, which is available (including a free trial download) at http://www.software3d.com/Stella.php. It can also be viewed as a compound of the rhombic dodecahedron and another polyhedron, but I haven’t been able to identify that second polyhedron — at least, not yet. If you know what the orange polyhedron is, please leave a comment with its name.
The convex hull of this solid is the cuboctahedron. To me, it looks like a hybrid of that solid, and the Stella Octangula. I created it using Stella 4d, which is available (including a free trial download) at http://www.software3d.com/Stella.php.
Each of the smaller pictures below may be enlarged by clicking on them.
All of these images were produced using Stella 4d, which you may try or buy at http://www.software3d.com/Stella.php.
This one is a variant of the icosidodecahedron.
This one is based on the rhombcuboctahedron.
This one is made of squares, rhombi, and irregular pentagons.
This one is composed entirely of pentagons and hexagons, none of which are regular.
This one has faces which include squares, rhombi, and isosceles triangles.
In this one, the hexagons and squares are regular. Only the isosceles triangles are irregular.
This is the dual of the last one shown here. Its faces are all either kites or rhombi.
I hoped to make this one into a near miss to the Johnson solids, but the octagons of both types, especially, are too far from regularity to get that to work. The only faces which are regular are the green triangles.
This one is a variant of the icosahedron.
I found this one interesting.
And this one is its dual:
Finally, here’s one made of kites and regular hexagons.
In this variation of the snub cube, twenty of the triangular faces have been excavated with short triangular pyramids. Since the snub cube is chiral, it’s possible to make a compound out of it and its mirror-image:
A polyhedron which is somewhat similar to the first one shown here can be produced by faceting a snub cube:
Stella 4d was used to create these images. You can find this program at http://www.software3d.com/Stella.php.
The Stella Octangula is another name for the compound of two tetrahedra. In this variant, each triangular face is replaced by a panel of three irregular pentagons. I used Stella 4d to make it, and you can find that program at http://www.software3d.com/Stella.php.
I’ve done quite a bit on this blog involving modifiying polyhedra via augmentation, in which polyhedra are attached to faces of another polyhedra. This was made using the opposite process, excavation, where parts of a given polyhedron are removed. First, a pentagonal pyramid was excavated from each pentagonal face of the icosidodecahedron. Next, octahedra were excavated from each triangular face. Finally, the bottom face of each of these octahedra was hidden, making it possible to see all the way through this solid. I constructed this with Stella 4d, software you can try or buy at www.software3d.com/Stella.php.
Here’s the same polyhedron again, but with a different color-scheme.
If one starts with a cuboctahedron, and then creates a zonish polyhedron from it, adding zones (based on the faces) to the faces which already exist, here is the result, below, produced by Stella 4d: Polyhedron Navigator (software you may buy or try at http://www.software3d.com/Stella.php):
The hexagons here, in this second image, are visibly irregular. The four interior hexagon-angles next to the octagons each measure more than 125 degrees, and the other two interior angles of the hexagons each measure less than 110 degrees — too irregular for this to qualify as a near-miss to the Johnson solids. However, Stella includes a “try to make faces regular” function, and applying it to the second polyhedron shown here produces the polyhedron shown in a larger image, at the top of this post.
It is this larger image, at the top, which I am proposing as a new near-miss to the 92 Johnson solids. In it, the twelve hexagons are regular, as are the eight triangles and six octagons. The only irregular faces to be found in it are the near-squares, which are actually isosceles trapezoids with two angles (the ones next to the octagons) measuring ~94.5575 degrees, and two others (next to the triangles) measuring 85.4425 degrees. Three of the edges of these trapezoids have the same length, and this length matches the lengths of the edges of both the hexagons and octagons. The one side of each trapezoid which has a different length is the one it shares with a triangle. These triangle-edges are ~15.9% longer than all the other edges in this proposed near-miss.
My next step is to share this find with others, and ask for their help with these two questions:
Once I learn the answers to these questions, I will update this post to reflect whatever new information is found. If this does qualify as a near-miss, it will be my third such find. The other two are the tetrated dodecahedron (co-discovered, independently, by myself and Alex Doskey) and the zonish truncated icosahedron (a discovery with which I was assisted by Robert Webb, the creator of Stella 4d).
More information about these near-misses, one of my geometrical obsessions, may be found here: https://en.wikipedia.org/wiki/Near-miss_Johnson_solid
RobertLovesPi.net 