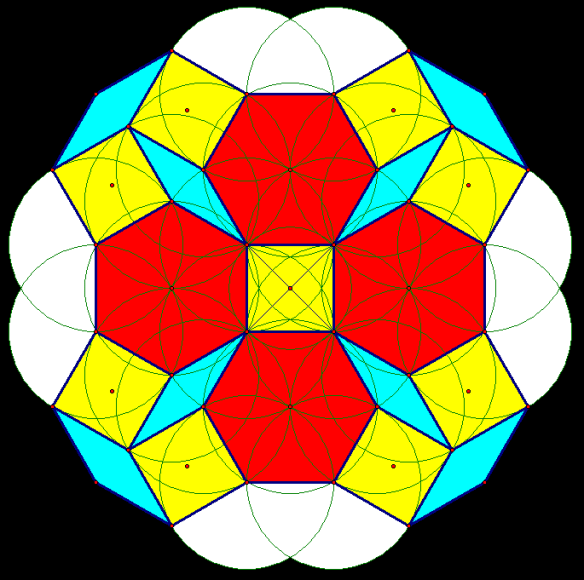
This is the fourth in a series of posts, each of which builds upon the others. The images in the prior three posts were created using Geometer’s Sketchpad and MS-Paint. For this one, I used Stella 4d to project the most recent of these images of each pentagonal face of an icosidodecahedron, and then rendered the triangular faces invisible. (Stella 4d is available for sale, with a free trial download available, at http://www.software3d.com/Stella.php.)
This is the inverted-color version of the previous post.
To see a single four-part compound eye, look at the previous post.
You’re standing on the mainland of North America — not on an island. From where you are, you can travel due East, and you’ll come to the Pacific Ocean. If you travel due West, however, you will come to the Atlantic Ocean. What’s more, this is true for a relatively large percentage of locations in the country where you are located — a greater percentage than would be the case for any other country on the North American continent, if there even are others.
In what country are you standing?
(Scroll down for the answer.)
.
.
.
.
.
.
.
.
.
.
.
You’re in Panama! Now, before anyone protests that Panama is in Central America, not North America, let me point out that Central America is part of the North American continent, just as Europe and India are part of the Eurasian continent. (Yes, I looked them up.)
If anyone is inside this polyhedron, they can see you!
Software credit: see www.software3d.com/Stella.php.
I used Stella 4d: Polyhedron Navigator to make this. You can try this program as a free trial download at www.software3d.com/Stella.php.
The images on the faces of this icosahedron appeared on this blog three posts ago, and were created with Geometer’s Sketchpad and MS-Paint. To project this image onto this polyhedron, and then generate this rotating .gif, I used a third program, Stella 4d. You may try this last program yourself, as a free trial download, at www.software3d.com/Stella.php.
In how many ways can different numbers of right angles appear in convex heptagons?
Heptagons do not have to have right angles at all, of course. If a heptagon has exactly one right angle, only one arrangement is possible: a right angle, and six oblique angles (“oblique” means non-right, so it includes both acute and obtuse angles).
With two right angles, there are three possibilities. In the first one shown, the right angles are consecutive. In the second, one oblique angle appears between the right angles. In the third, two oblique angles appear between the right angles. Increasing two oblique angles to three is simply a repeat of the third three-right angle heptagon, so this set stops with exactly three members.
With three right angles, I have found four possibilities: (1) all three right angles appear consecutively; (2) two right angles are consecutive, and one of them has one oblique angle between it and the third right angle; (3) two right angles are consecutive, and each of them has two oblique angles between it and the third right angle; and (4) None of the three right angles is consecutive. In this heptagon, the number of oblique angles which appear between the three different right-angle pairs are one, one, and two.
I have found no others, and, after searching to exhaustion, I do not think any other arrangement of right and oblique angles in a convex heptagon is possible. However, this is a conjecture, not a proof, and may, in fact, be incorrect. If you can provide proof that this listing of possibilities is complete, or a counterexample to show that it is not, please leave a comment with details.
RobertLovesPi.net 