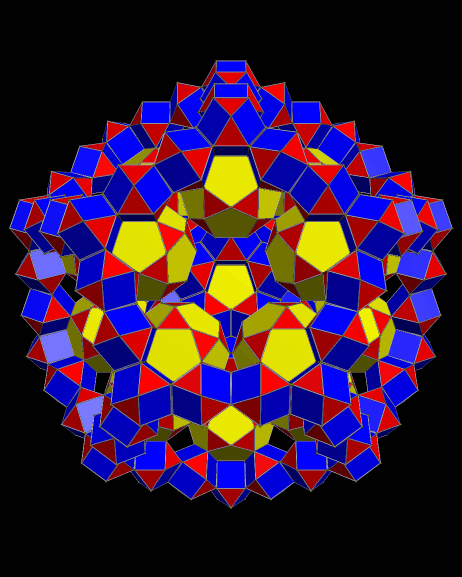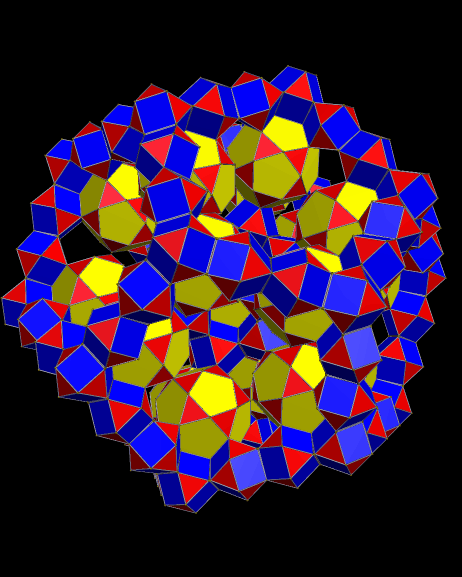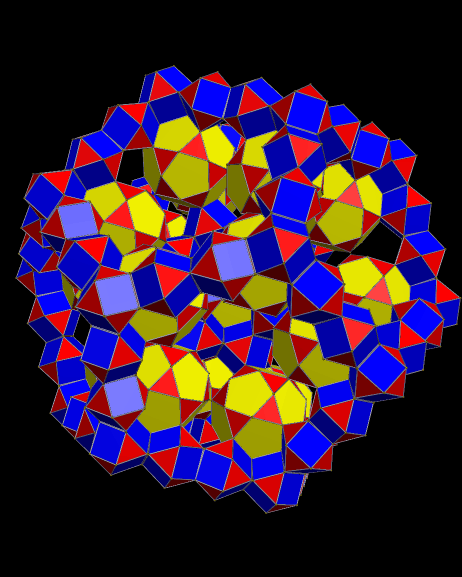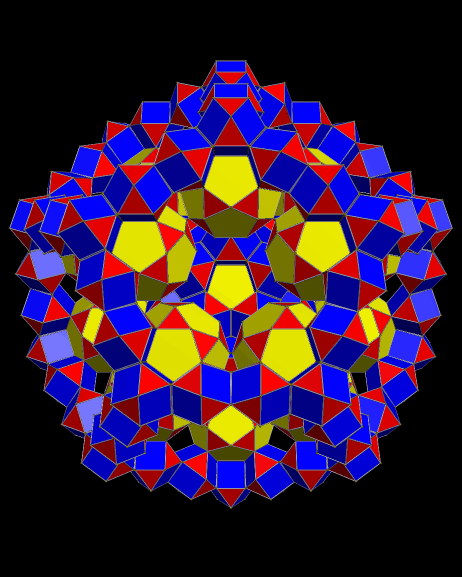
These are the third (above) and fifth (below) stellations of the triamond pentagonal bifrustrum, which I previously posted here: https://robertlovespi.wordpress.com/2014/07/30/my-lost-discovery-from-2006-the-triamond-pentagonal-bifrustrum/. These rotating images are made with Stella 4d, a program available at www.software3d.com/Stella.php.
The images on the faces of this polyhedron are based on information sent from NASA’s Lunar Reconnaisance Orbiter, as seen at http://lunar.gsfc.nasa.gov/lola/feature-20110705.html and tweeted by @LRO_NASA, which has been happily tweeting about its fifth anniversary in a polar lunar orbit recently. I have no idea whether this is actually an A.I. onboard the LRO, or simply someone at NASA getting paid to have fun on Twitter.
To get these images from near the Lunar South Pole onto the faces of a rhombic enneacontahedron, and then create this rotating image, I used Stella 4d: Polyhedron Navigator. There is no better tool available for polyhedral research. To check this program out for yourself, simply visit www.software3d.com/Stella.php.
Music: the first two tracks from the Murder By Death album Like the Excorcist, But More Breakdancing. Please visit their website, http://www.murderbydeath.com, to buy this band’s music and merchandise. While you’re there, I recommend checking their concert calendar, to see if they may be playing near you soon. Murder By Death concerts, which I’ve seen six times now, are not to be missed!
Visuals: rotating polyhedra, all with icosidodecahedral symmetry, generated using Stella 4d: Polyhedron Navigator, which you can try for yourself at http://www.software3d.com/Stella.php. The polyhedra shown are, in order of appearance:
I’ve posted polyhedral cages before — it simply never occurred to me to call such objects by that term. I often tag them as art / geometrical art, rather than mathematics, for they are not true polyhedra, by the generally accepted definition, where edges must involve faces meeting in pairs. Polyhedral cages do not follow this rule, so calling them mathematics causes problems. To do mathematics, after all, is to play games with numbers, and other ideas, according to the rules, with these rules being discovered as we discover new theorems. The rules are respected for one reason alone: we know they work. If one breaks these rules with, say, a geometric figure, on aesthetic grounds, one is crossing the boundary between mathematics and geometrical art.
The reason for hiding faces of polyhedra is usually aesthetic, not mathematical. I use software called Stella 4d, available at www.software3d.com/Stella.php, to manipulate polyhedra in numerous different ways, trying to discover “new” polyhedra — new, that is, in the sense that these discoveries (not inventions) were never seen before I saw them on my computer screen. When you see a rotating geometrical picture on this blog, such as any of the ones at the bottom of this post, it was created using Stella.
Every now and then, I stumble upon a polyhedron which would look better if selected faces were simply made to disappear — and with Stella, that’s easy. They still exist in the polyhedron, in Stella‘s “mind,” but are rendered invisible in the on-screen image, thus creating the appearance of holes in the polyhedron’s surface. If these holes are regarded as real — “real” in the somewhat confusing sense that there’s nothing where the holes are, holes being absences of what surrounds them — then the former polyhedron is now a polyhedral cage. Here are several examples.
I made this using Stella 4d: Polyhedron Navigator, software you may try for yourself at http://www.software3d.com/Stella.php.
I made all of these using Stella 4d: Polyhedron Navigator. You may try this software for yourself at www.software3d.com/Stella.php.
It isn’t difficult to find rankings for the most massive objects in the solar system, rankings of objects in terms of increasing distance from the sun, or rankings of objects by radius. However, ranking objects by surface gravitational field strength is another matter, and is more complicated, for it is affected by both the mass and radius of the object in question, but in different ways. If two objects have different masses, but the same radius, the gravitational field strength will be greater for the more massive object. However, increasing the radius of an object decreases its surface gravitational field strength, in an inverse-square relationship.
Gravitational field strength is measured in N/kg, which are equivalent to m/s², the units for acceleration. The terms “gravitational field strength” and “acceleration due to gravity,” both of which are symbolized “g,” are actually synonymous. I prefer “gravitational field strength” because referring to acceleration, when discussing the weight of a stationary object on the surface of a planet, can cause confusion.
Use of the numbers given below is easy: given the mass of a thing (an imaginary astronaut, for example), in kilograms, simply multiply this figure by the given gravitational field strength, and you’ll have the weight of the thing, in newtons, on the surface of that planet (or other solar system object). If, for some odd reason, you want the weight in the popular non-metric unit known as the “pound,” simply divide the weight (in newtons) by 4.45, and then change the units to pounds.
How is surface gravitational field strength determined? To explain that, a diagram is helpful.
The large green circle represents a planet, or some other solar system object, and the blue thing on its surface, which I’ll call object x, can be pretty much anything on the solar system object’s surface. There are two formulas for Fg, the force of gravity pulling the planet and the thing on its surface toward each other. One is simply Fg= mxg, a form of Newton’s Second Law of Motion, where “g” is the gravitational field strength, and mx is the mass of the object at the surface. The other formula is more complicated: Fg= (Gmxmp)/r². This is Newton’s Law of Universal Gravitation, where “G” (not to be confused with “g”) is the universal gravitational constant, 6.67259 x 10-11 Nm²/kg², and mp and r are the mass and radius of the planet (or other solar system object). Because they each equal Fg, the expressions mxg and (Gmxmp)/r² can be set equal to each other, yielding the equation mxg = (Gmxmp)/r², which becomes g = (Gmp)/r² after mx is cancelled. The mass of the object on the surface is not needed — “g” is simply a function of mp and r.
There is a problem, however, with the idea of “surface” gravitational field strength — and that is the fact that the five largest objects in the solar system, the sun and the gas giants, all lack visible solid surfaces. One cannot stand on Jupiter — if you tried, you’d simply fall inside the planet. Therefore, for Jupiter, picture a solid platform floating at the top of the visible clouds there, and place the test object on this solid platform. Under those conditions, multiplying the test object’s mass by the Jovian value of “g” will, indeed, yield the weight of the object there, as it could be measured by placing it on a bathroom scale, at rest on the floating platform. For the other gas giants, as well as the sun, the idea is the same.
The objects included in the list below are the sun, all eight major planets, all dwarf planets (and dwarf planet candidates) with known values of “g,” all major satellites, some minor satellites, and a few of the largest asteroids. Many more objects exist, of course, but most have values for “g” which are not yet known.
Here are the top five:
Sun/Sol, 274.0 N/kg
Jupiter, 24.79 N/kg
Neptune, 11.15 N/kg
Saturn, 10.44 N/kg
Earth/Terra, 9.806 65 N/kg
The top five, alone, make me glad I undertook this project, for I did not realize, before doing this, that our planet has the highest surface gravitational field strength of any object in the solar system with a visible solid surface.
The next five include the rest of the major planets, plus one Jovian moon.
Venus, 8.87 N/kg
Uranus, 8.69 N/kg
Mars, 3.711 N/kg
Mercury, 3.7 N/kg
Io, 1.796 N/kg
The third set of five are all planetary moons, starting with earth’s own moon. The others are Jovian moons, except for Titan, which orbits Saturn.
Moon/Luna, 1.622 N/kg
Ganymede, 1.428 N/kg
Titan, 1.352 N/kg
Europa, 1.314 N/kg
Callisto, 1.235 N/kg
The fourth set of five begins with the largest dwarf planet, Eris, and includes two other dwarf planets as well.
Eris, 0.827 N/kg (dwarf planet)
Triton, 0.779 N/kg (Neptune’s largest moon)
Pluto, 0.658 N/kg (dwarf planet)
Haumea, 0.63 N/kg (dwarf planet)
Titania, 0.38 N/kg (largest moon of Uranus)
The fifth set of five includes the remaining dwarf planets with known values of “g.”
Oberon, 0.348 N/kg (moon of Uranus)
1 Ceres, 0.28 N/kg (dually classfied: dwarf planet and largest asteroid)
Charon, 0.278 N/kg (largest moon of Pluto)
Ariel, 0.27 N/kg (moon of Uranus)
90482 Orcus, 0.27 N/kg (probable dwarf planet)
The sixth set of five are dominated by Saturnian moons.
Rhea, 0.265 N/kg (Saturnian moon)
4 Vesta, 0.25 N/kg (2nd largest asteroid)
Dione, 0.233 N/kg (Saturnian moon)
Iapetus, 0.224 N/kg (Saturnian moon)
Umbriel, 0.2 N/kg (moon of Uranus)
The seventh set of five are mostly asteroids.
704 Interamnia, 0.186 N/kg (5th most massive asteroid)
2 Pallas, 0.18 N/kg (3rd most massive asteroid)
Tethys, 0.147 N/kg (Saturnian moon)
52 Europa, 0.14 N/kg (7th most massive asteroid)
3 Juno, 0.12 N/kg (large asteroid, w/~1% of mass of the asteroid belt)
Starting with the eighth group of five, I have much less certainty that something may have been omitted, although I did try to be thorough. My guess is that most future revisions of this list will be necessitated by the discovery of additional dwarf planets. Dwarf planets are hard to find, and there may be hundreds of them awaiting discovery.
Enceladus, 0.114 N/kg (Saturnian moon)
Vanth, 0.11 N/kg (moon of probable dwarf planet 90482 Orcus)
10 Hygiea, 0.091 N/kg (4th most massive asteroid)
15 Eunomia, 0.08 N/kg (large asteroid, with ~1% of mass of asteroid belt)
Miranda, 0.079 N/kg (moon of Uranus)
Here is the ninth group of five:
Nereid, 0.072 N/kg (Neptunian moon; irregular in shape)
Proteus, 0.07 N/kg (Neptunian moon; irregular in shape)
Mimas, 0.064 N/kg (Saturnian moon / smallest gravitationally-rounded object in the solar system)
Puck, 0.028 N/kg (6th largest moon of Uranus)
Amalthea, 0.020 N/kg (5th largest Jovian moon)
Finally, here are “g” values for the two tiny moons of Mars, included because they are nearby, and are the only moons Mars has to offer. A more exhaustive search would reveal many asteroids and minor satellites with “g” values greater than either Martian moon, but smaller than Amalthea, the last solar system object shown in the last set of five.
Phobos, 0.0057 N/kg
Deimos, 0.003 N/kg
RobertLovesPi.net 