At least in this part of the world, “How are you today?” — or variations thereof — is commonly used as a way to start conversations, as a bit of “small talk.” The odd part of this social convention is that, when people ask this, they usually don’t really want to hear an honest answer — or, indeed, any answer at all that isn’t part of the standard “small talk” script.
The usual answer (“Fine, thanks,” or something like it) is yet another empty phrase — more small talk. Unusual answers, though, have great potential for fun. I first encountered this idea in a class I took, many years before, where the teacher told us that his habit was to answer, instead, with an upbeat, “Getting better!” I’ve tried this, and the facial expressions often seen, in response, are indeed quite entertaining. Small talk is annoying — to me, anyway — but disrupting it, by simply deviating from the usual script, can be a lot of fun.
Here are some other possible answers, but this game is probably most fun if you make up your own.
- “I’m glad you asked. Actually, my feet hurt. Do you know why?”
- “Well, I’d feel a lot better if I hadn’t just blown my whole budget for the week on chocolate. It tasted good when I ate it all for breakfast this morning, though!”
- “Hopefully, I’ll be able to answer your question in a few minutes. Say, where’s the nearest restroom?”
- “Terrible. My beloved pet cricket just died.”
- “I’m hoping it gets better soon. Could you recommend a good mechanic nearby, as well as a chiropractor?”
- “I’m feeling great! There is nothing like a couple of extra-strength placebos to start the day!”
- “I’m okay now, but I’m not looking forward to this afternoon at all. You have heard about the giant asteroid heading straight for us, right? It’s supposed to hit somewhere near downtown, at about four o’clock.”
- “Well, I’m broke. May I borrow fifty bucks until next month?”
While I do greatly value honesty, I obviously exclude jokes from the category of lies. Also, suggestions for other funny responses, in comments, would be much appreciated.
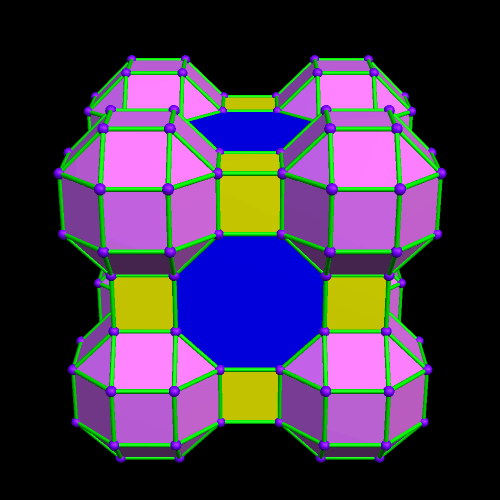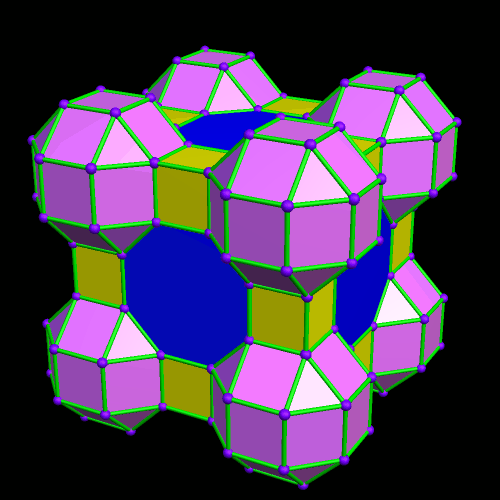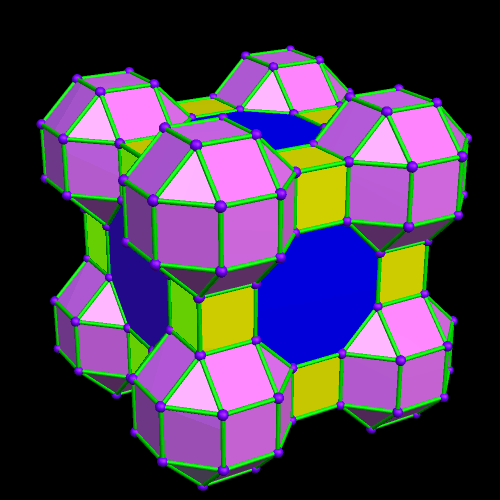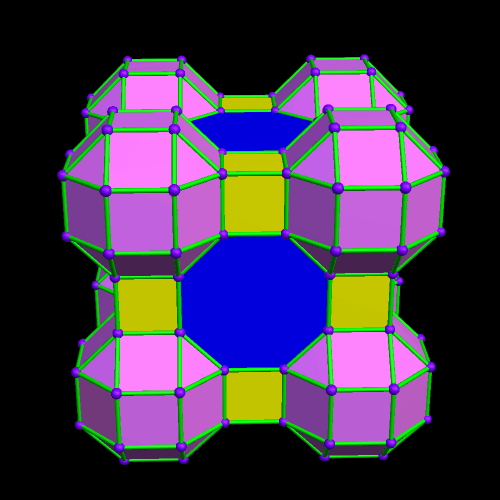
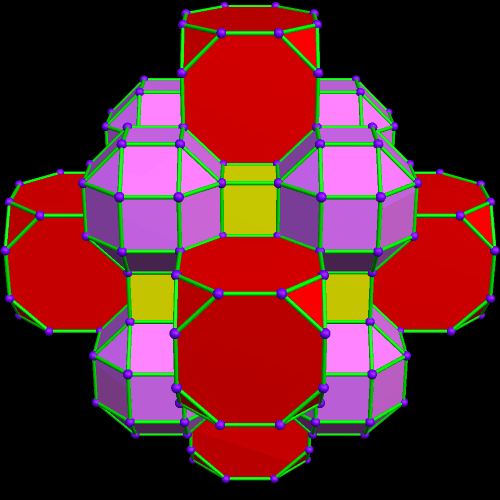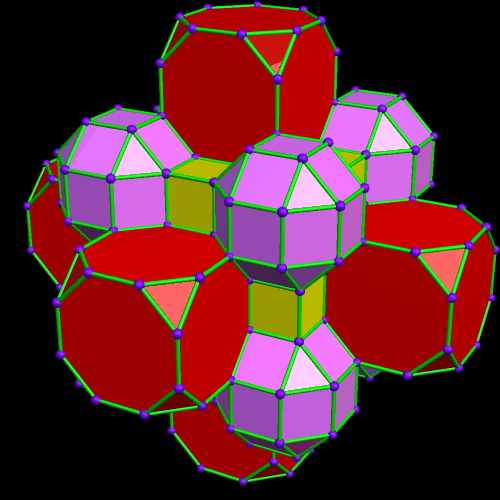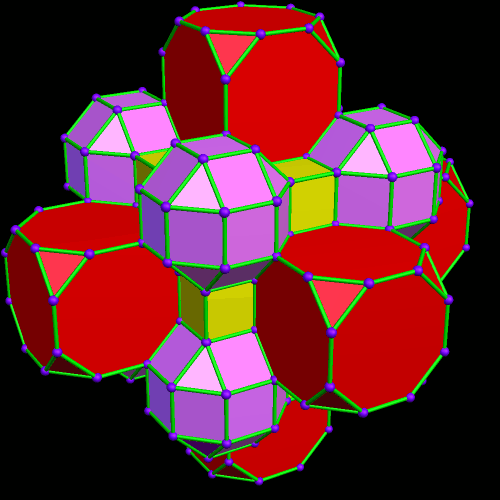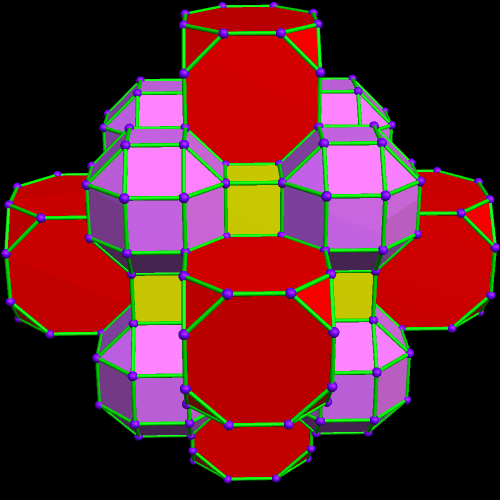
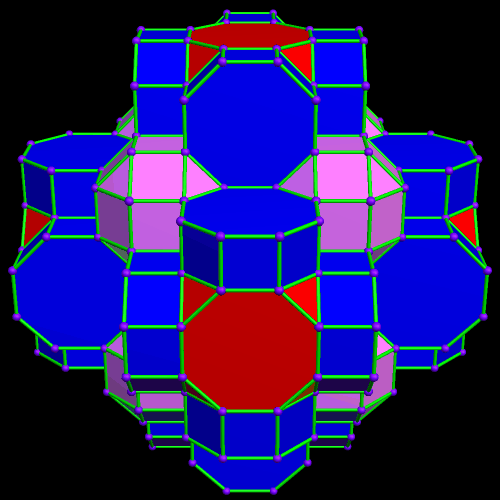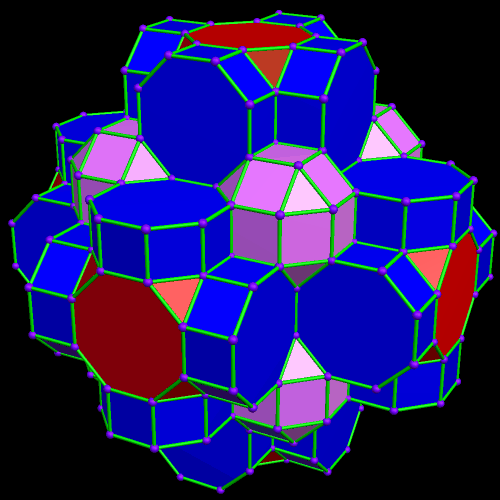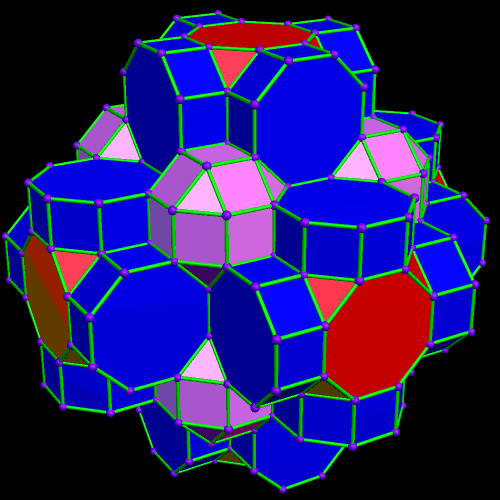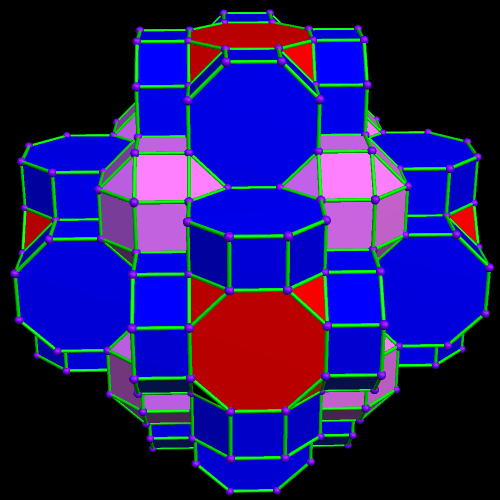
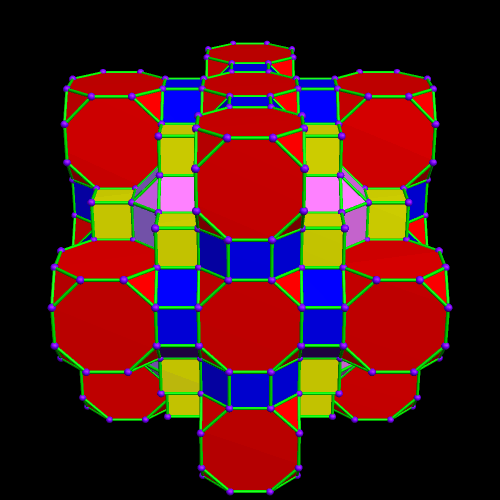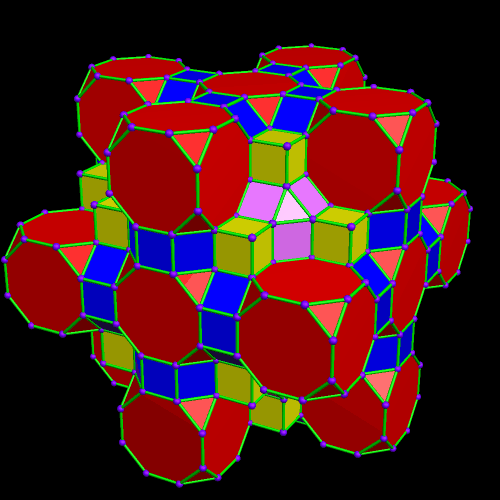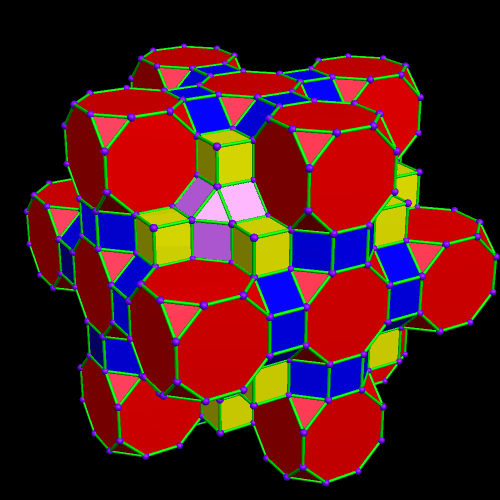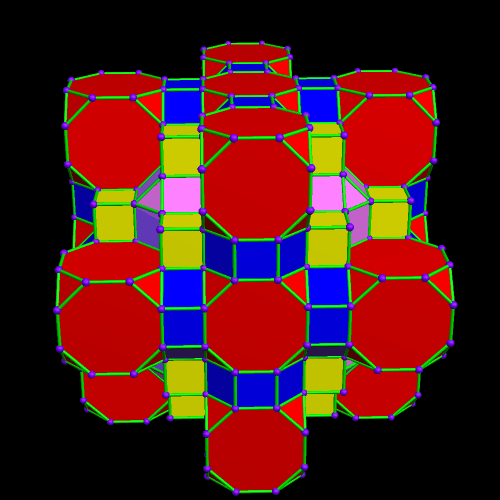
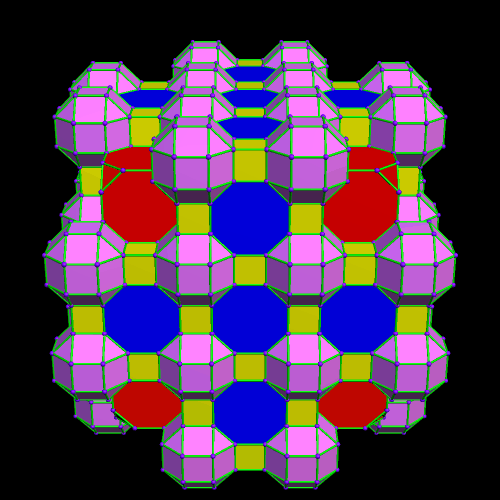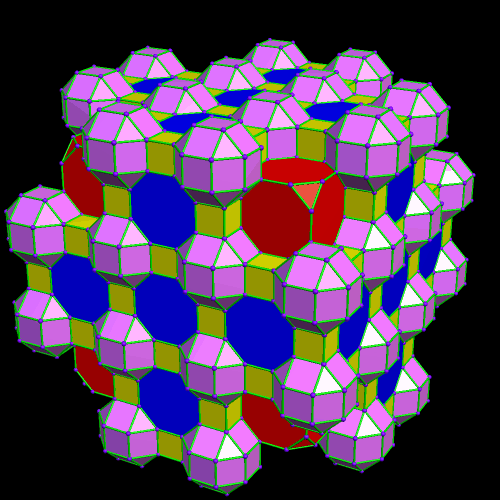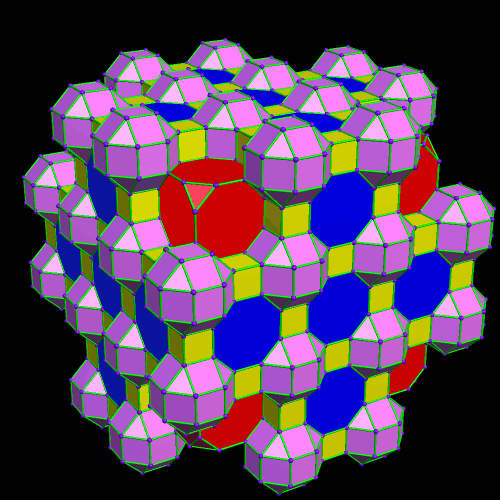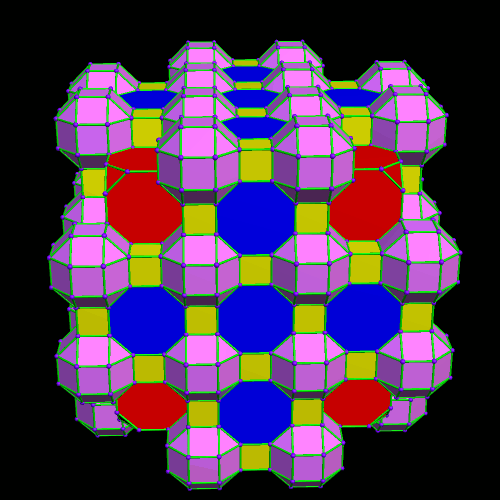
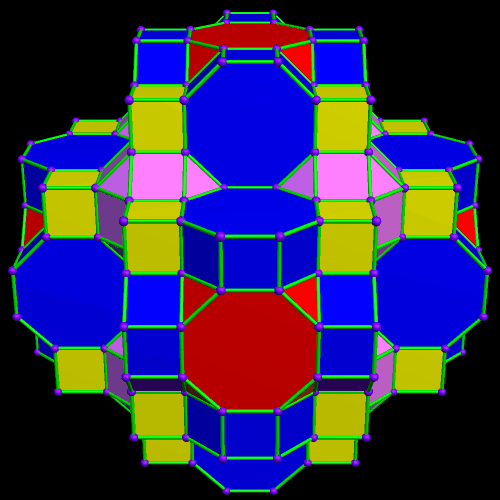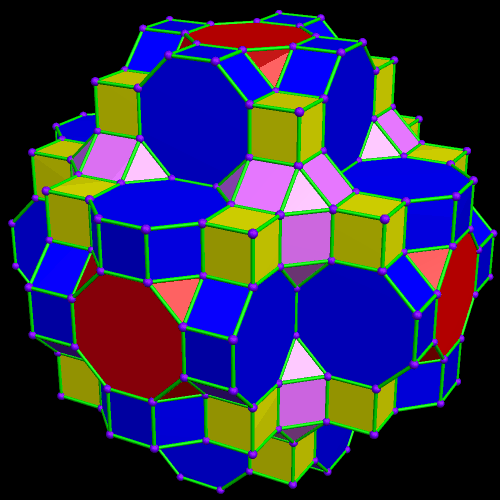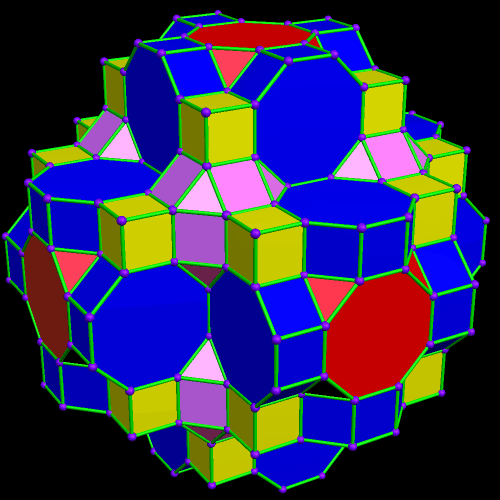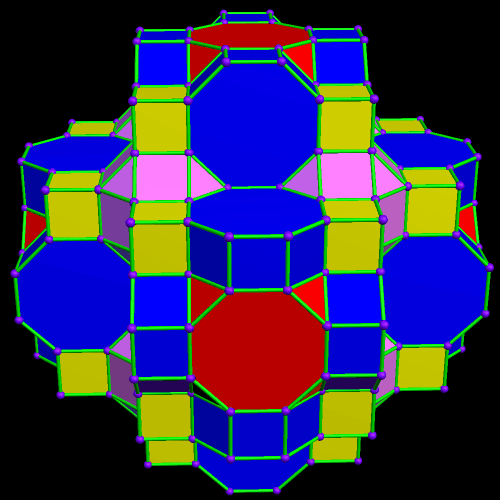 This was an accidental discovery I made, just messing around with Stella 4d, a program you may try for yourself at http://www.software3d.com/Stella.php. The next cells added will be red truncated cubes.
This was an accidental discovery I made, just messing around with Stella 4d, a program you may try for yourself at http://www.software3d.com/Stella.php. The next cells added will be red truncated cubes. The next set of polyhedra added: some yellow cubes, and blue octagonal prisms.
The next set of polyhedra added: some yellow cubes, and blue octagonal prisms.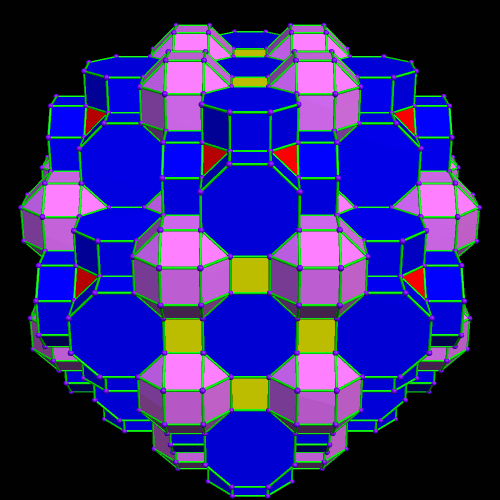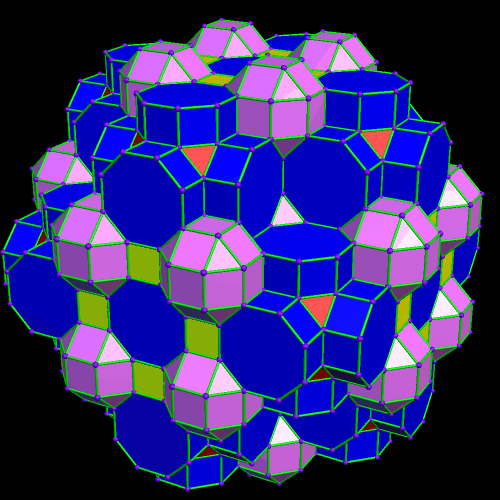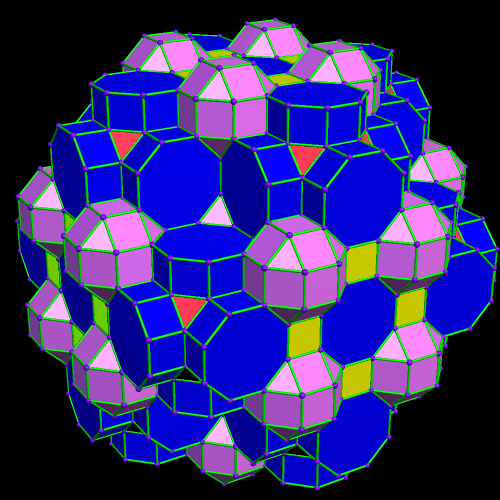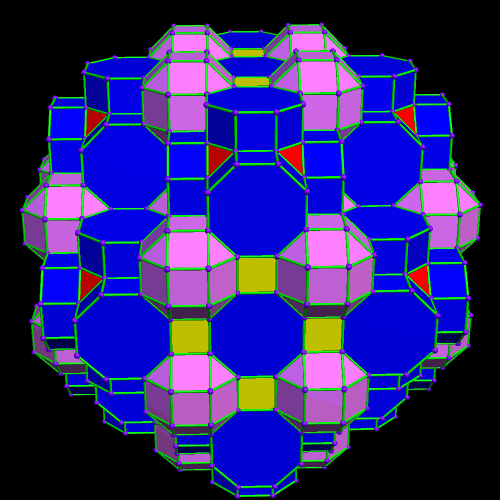 Now I’ll add more of the red truncated cubes.
Now I’ll add more of the red truncated cubes. At this point, more yellow cubes are needed.
At this point, more yellow cubes are needed. The next polyhedra added will be pink rhombcuboctahedra.
The next polyhedra added will be pink rhombcuboctahedra.